|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Доходность и риск
Доходность всегда относится к конкретному периоду времени. Например, 1 тыс. рублей можно заработать за месяц, а можно и за год. Даже расчет относительного показателя доходности не сделает эти цифры сопоставимыми. Если продолжить пример и предположить, что вложение 10 млн. рублей принесло доход в 1 тыс. рублей за 1 неделю, а инвестирование 10 тыс. рублей обеспечило такой же доход за 6 месяцев, то полученные выше значения доходности будут недостаточно объективны. Для обеспечения сопоставимости этих показателей, их необходимо привести к единой временной базе. В финансах доходность обычно приводится к годовому исчислению, то есть исходные данные аннуилизируются. Сравнивая формулы расчета доходности и формулу годовой процентной ставки (2.2.1), можно заметить их идентичность. И доходность, и процентная ставка отражают темп прироста первоначально вложенных сумм. Рассчитывая доходность, по сути дела определяют величину соответствующей процентной ставки.
Существуют различные способы начисления процентов и, соответственно, различные процентные ставки. Наращение по простой и сложной ставкам приводит к различным результатам. Какая конкретно ставка должна использоваться при определении годовой доходности? В финансах принято в качестве измерителя доходности использовать эффективную сложную процентную ставку, то есть годовую ставку, предполагающую однократное в течение года реинвестирование начисленных процентов. Однако для краткосрочных финансовых операций (продолжительностью менее 1 года) допускается применение простой процентной ставки. Так, например, доходность ГКО рассчитывалась по ставке простых процентов (формула 2.2.14) в предположении, что продолжительность года составляет 365 дней. Безусловно, такая неоднозначность осложняет жизнь финансисту, однако возникающие трудности не следует абсолютизировать. Прежде всего необходимо понять, что способ аннуилизации доходности ни в коей мере не влияет на реальные параметры рассматриваемой финансовой операции. Доходность является абстрактным показателем, применяемым для обеспечения сопоставимости и сравнительной оценки различных вложений капитала. Поэтому, сравнивая между собой две инвестиции по уровню их доходности, важно убедиться в сопоставимости методик расчета этих показателей. Вопрос о том, какой из способов расчета лучше или "правильнее" не является самым важным. Необходимо, чтобы для обеих операций использовался один и тот же способ аннуилизации.
Продолжая пример, рассчитаем доходность двух вложений различными способами (в обоих случаях продолжительность года составляет 365 дней):
-
по эффективной ставке сложных процентов. По формуле (2.2.15) находим:
для
 ,
, 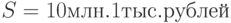 ,
,  (1 неделя)
(1 неделя)
для
 ,
,  ,
,  (6 месяцев)
(6 месяцев)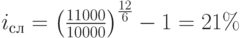
-
по простой процентной ставке. По формуле (2.2.12) находим:
для
 ,
, 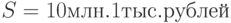 ,
, 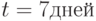 ,
, 

для
 ,
,  ,
,  .,
.,  .
.
Применив формулу эквивалентности простой и сложной процентных ставок (2.2.21), получим аналогичные результаты:
для


для

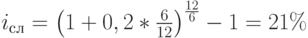
С позиций финансовой теории обоснованным является использование сложной процентной ставки, так как данный метод учитывает возможность реинвестирования начисленных процентов. Но в ряде случаев расчет доходности производится в соответствии с принятыми на данном рынке обычаями. Общим правилом является использование простой процентной ставки для краткосрочных финансовых операций (депозитные сертификаты, казначейские векселя, краткосрочные ссуды и т.п.). Во всех остальных случаях используется эффективная сложная процентная ставка. Следует отметить, что использование эффективной сложной ставки для расчета доходности также не свободно от недостатков. Предположение об однократном реинвестировании начисленных процентов нуждается в обосновании. Более логичным было бы предположение о непрерывной капитализации процентов, то есть расчет доходности по ставке сложных непрерывных процентов.
Рассмотрим несколько примеров расчета доходности краткосрочных инвестиций (продолжительностью менее 1 года). Как уже отмечалось, в данном случае применяется ставка простых процентов, поэтому большое значение имеет способ подсчета числа дней в периоде, а также метод определения продолжительности года (временной базы). Подробнее об этом говорилось в "Временная стоимость денег" По 90-дневному банковскому депозитному сертификату, купленному за 10 тыс. рублей, в конце срока его действия получен доход в сумме 1 тыс. рублей. Фактическая доходность за 90 дней составила 10% (1 000 / 10 000), годовая доходность в предположении, что год равен 360 дням будет равна 40%:
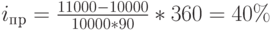
Если предположить точную временную базу (  = 365 дней), то доходность операции составит 40,56%. Допустим, что данный сертификат был приобретен дороже номинала – за 10 тыс. 200 рублей и продан через 45 дней за 10 тыс. 800 рублей. Тогда его фактическая годовая доходность (при
= 365 дней), то доходность операции составит 40,56%. Допустим, что данный сертификат был приобретен дороже номинала – за 10 тыс. 200 рублей и продан через 45 дней за 10 тыс. 800 рублей. Тогда его фактическая годовая доходность (при  = 360) составит 47,06%:
= 360) составит 47,06%:

Если по условиям сертификата на него начислялись простые проценты из расчета 25% годовых, то сначала следует найти их общую сумму, причитающуюся владельцу за 45 дней. Применив формулу (2.1.3), получим:
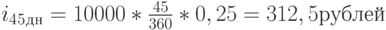
Тогда общий доход от владения сертификатом в течение 45 дней составит 912,5 рублей (10 800 – 10 200 + 312,5), а полная годовая доходность владения этим инструментом (hpr) 71,57%:

Таким образом, рассчитывая фактическую доходность, прежде всего необходимо выявить все доходы, полученные от инвестиции как в форме текущих выплат, так и в виде прироста стоимости инвестиций, а затем разделить их на начальные инвестиции (фактически вложенный капитал). Полученная величина аннуилизируется путем умножения на принятую временную базу и деления на длительность операции.
Данное правило полезно помнить при определении доходности финансовых инструментов, продаваемых со скидкой (дисконтом). В этом случае не следует путать учетную ставку, устанавливаемую по данному инструменту (процент скидки) с величиной доходности. Ставка дисконта служит для определения суммы дохода в абсолютном выражении (рублях). Только найдя эту сумму, можно приступать к расчету доходности инструмента. Например, вексель номиналом 50 тыс. рублей продается по курсу 85%, т.е. с дисконтом 15%. Он будет выкуплен через 60 дней по номиналу. Следовательно, через 2 месяца инвестор получит доход в сумме 7,5 тыс. рублей (50 х 0,15). Доходность этой операции составит (при t = 360 дней) 105,88%:
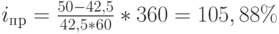
То есть, ставка дисконта, установленная по векселю не отражает его фактической доходности, а является номинальной величиной, используемой только для определения абсолютной суммы дохода. Это относится и к случаю, когда ставка дисконта установлена в годовом исчислении. Например, по вышеупомянутому векселю известен его номинал, срок и годовая учетная ставка 60%. Тогда, применив формулу банковского учета (2.1.8), сначала найдем продажную стоимость векселя:
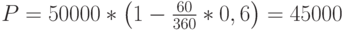
Следовательно, фактический доход инвестора составит 5 тыс. рублей (50 000 – 45 000), а фактическая годовая доходность операции – 66,67%:

Если известна доходность за период, меньший, чем год (месяц, 40 дней, полугодие и т.д.), то годовую доходность можно определить умножив имеющиеся данные на число периодов в году: доходность за месяц умножается на 12, квартальная доходность – на 4 и т.д. Данный способ аннуилизации применим только в случае использования простой процентной ставки. Например, доходность за 75 дней составила 5%, временная база – 365 дней. Тогда годовая доходность будет равна 24,33% (5 х 365 / 75). Как уже отмечалось выше, способ расчета дохода не влияет на параметры финансовой операции. То есть, фактические денежные потоки, порождаемые операцией, являются входными переменными и не зависят от того, какие арифметические действия выполняет над их величинами финансист, чтобы определить доходность. Поэтому, ничто не мешает финансовому менеджеру рассчитать доходность одной и той же операции различными способами. Для этого следует применить формулы расчета эквивалентных процентных ставок (см. "Временная стоимость денег" ). В предыдущем примере годовая доходность векселя как ставка простых процентов составила 66,67%. Применив формулу (2.2.21), определим эквивалентную ей сложную процентную ставку:
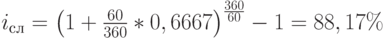
Применив формулу (2.2.29) можно рассчитать годовую доходность по сложной непрерывной ставке (силе роста):

То есть, одна и та же операция, приносящая инвестору 5 тыс. рублей дохода на вложенные 45 тыс. рублей через 60 дней, может быть охарактеризована следующими показателями доходности:
- по ставке простых процентов (
 ) – 66,67%;
) – 66,67%; - по эффективной сложной процентной ставке (
 ) – 88,17%;
) – 88,17%; - по сложной непрерывной процентной ставке (силе роста
 ) – 63,22%.
) – 63,22%.
Так как данная операция является краткосрочной, то для ее оценки более приемлем первый показатель доходности (по ставке простых процентов). Однако финансовый менеджер может с успехом использовать и два других измерителя доходности для сравнения с параметрами иных операций, осуществляемых предприятием.
