|
есть желание заново пройти курс "Тестирование в современном высшем образовании"
|
Обоснование качества теста
5.4. Распределения, гипотезы и адаптивное тестирование
Располагая каким-то распределением данных тестирования, можно исследовать возможность описания этой совокупности каким-то типовым распределением, если тип распределения неизвестен, а затем найти (идентифицировать) неизвестный параметр (параметры) распределения, а также эффективность того или иного описания. Неправильный выбор модели обработки данных тестирования и процедуры тестирования может привести к существенной ошибке в результатах или выводах.
Технология адаптивного тестирования (методология IRT) опирается на центральную идею: тестовые задания следует адаптировать по трудности к уровню подготовки тестируемой группы – по той или иной заранее определенной технологии. Причем таким образом, чтобы повышать валидность профилей ответов испытуемых. Одинаково не нужны как слишком легкие, так и слишком сложные задания.
Если адаптационный механизм подобран адекватно, то он должен оптимизировать тест, сократить время тестирования, сохраняя или увеличивая точность измерений (сравнительно с неадаптивным тестированием).
В итоге, применение адаптивного тестирования предполагает не только генерацию, предъявление и оценку результатов выполненных адаптивных тестов, но и соответствующий анализ данных тестирования, особенно, представление в стандартизованной шкале баллов. Испытуемого, поднимающегося по шкале трудности в рамках тематического блока, "щадят" по трудности заданий в другом блоке, если он удается меньше.
Адаптивный алгоритм контроля знаний требует оценки статистических признаков и характеристик обучения динамически, на каждом шаге тестирования. Стратегия перехода на новый уровень, а, следовательно, и на новый уровень продуктивности обучения зависит от этого. Методы при тестировании "в глубину" позволяют определить, насколько велик пробел в знаниях обучаемого "в пределах данного распределения данных". Они также увеличивают устойчивость (а также и объективность) оценок трудности заданий, независимость их от свойств выборки, дифференцируемость ошибки измерения для оценок параметров всех испытанных и трудности заданий теста.
Пример. Можно по имеющимся результатам тестирования получить адекватную эмпирическую формулу зависимости одного фактора y от другого фактора x (например, x – число решенных заданий данной группы, y – граница оценки по заданиям данной группы). Ищем, например, модель типа модели Раша,
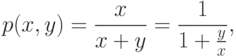
или
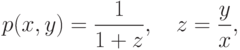
где p(x,y) – вероятность (мера успеха) того, что испытуемый с мерой уровня подготовки равной x правильно выполнит задание с мерой трудности y.
По результатам тестирования можно получить эмпирическую формулу зависимости одного фактора y от нескольких других факторов x1 , x2, …, xn (например, x – время, y – средняя оценка тестирования или x – число решенных заданий данной группы, y – граница оценки по заданиям данной группы).
Пример. Можно найти модель границы оценок 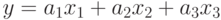 , где y – номер группы (по уровню подготовки) испытуемого, x1 – число выполненных трудных заданий, x2 – число выполненных средних заданий, x3 – число выполненных легких заданий. Данные yi, x1i, x2i, x3i по испытуемым i=1,2,…,n – заданы. Неизвестные коэффициенты a1, a2, a3 характеризуют веса тестовых баллов заданий каждого уровня при отнесении испытуемых в группу. Такая задача поможет шкалировать данные тестирования. В других случаях ищут квадратичную многофакторную зависимость.
, где y – номер группы (по уровню подготовки) испытуемого, x1 – число выполненных трудных заданий, x2 – число выполненных средних заданий, x3 – число выполненных легких заданий. Данные yi, x1i, x2i, x3i по испытуемым i=1,2,…,n – заданы. Неизвестные коэффициенты a1, a2, a3 характеризуют веса тестовых баллов заданий каждого уровня при отнесении испытуемых в группу. Такая задача поможет шкалировать данные тестирования. В других случаях ищут квадратичную многофакторную зависимость.
Дисперсионный анализ позволяет изучать степень влияния одного (нескольких) факторных признаков на результативный признак. Группируя данные наблюдения по интервалам, установить, какая группировка отвечает существенному различию качества отдельных групп тестированных.
Основная идея такого (дисперсионного) анализа заключается в разбивке суммы квадратов отклонений на несколько компонентов, каждый из которых соответствует действительной, или предполагаемой причине изменчивости средних значений.
В ходе дисперсионного анализа изучаются колебания лишь одного признака – результативного, а простейшим показателем колебания служит дисперсия, которая разлагается на внутригрупповую и межгрупповую составляющие. Межгрупповая дисперсия возникает под действием какого-либо фактора, который приводит к разным величинам средних, имеющихся в отдельных группах и отражает колебания этих средних. Внутригрупповая дисперсия возникает под действием прочих случайных факторов. Она отражает среднее колебаний внутри групп. При разбиении (разложении) общей дисперсии на две её составляющие, можно выделить ту часть, которая обусловлена действием одного фактора, затем другого, третьего и т.д.
Общая дисперсия признака – сумма квадратов отклонений всех вариантов результативного признака от общей его средней.
Пусть производится n измерений случайной величины y. Каждое тестовое измерение yi, i=1, 2, ..., n зависит от некоторого числа параметров xij, которые могут принимать дискретные или непрерывные значения. Эту зависимость представляют обычно в виде линейной комбинации параметров xij с коэффициентами bi и случайными ошибками измерения ei.
Таким образом, находим некоторую многофакторную зависимость:

Для однофакторного дисперсионного анализа данные представляют в виде:
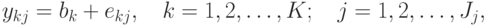
где k – номер уровня (группы), куда попало наблюдаемое значение ykj, K – число уровней, Jj – число попавших в класс номер j, bk – среднее значение по уровню номер k, ekj – ошибка для ykj. Затем находят общее среднее b и групповые средние bk:
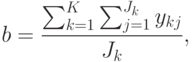
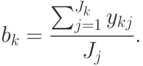
Далее находят дисперсию по факторам Df и общую (остаточную) дисперсию:
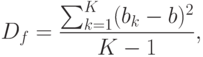
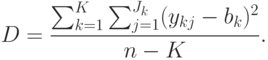
Значение отношения F=Df/D характеризует влияние факторного признака. Чем больше это влияние, тем больше значение F.
