Цепи Маркова
Теорема 10.1.
Если в полном ориентированном графе с  вершинами хотя бы две
вершины имеют одинаковые степени выхода, то в этом ориентированном графе найдутся
вершинами хотя бы две
вершины имеют одинаковые степени выхода, то в этом ориентированном графе найдутся  такие вершины, что дуги (ребра), соединяющие их, образуют
ориентированный цикл.
такие вершины, что дуги (ребра), соединяющие их, образуют
ориентированный цикл.
Задача 2. Турнир между  шахматистами закончился без ничьих. Можно
ли пронумеровать всех участников в таком порядке, чтобы оказалось, что
каждый выиграл партию у шахматиста, имеющего номер на единицу больше?
шахматистами закончился без ничьих. Можно
ли пронумеровать всех участников в таком порядке, чтобы оказалось, что
каждый выиграл партию у шахматиста, имеющего номер на единицу больше?
Решение. Достаточно выяснить, что всякий полный ориентированный граф
с  вершинами имеет простой путь, проходящий через все вершины
орграфа. Доказательство: проведем методом математической индукции по числу вершин
орграфа.
вершинами имеет простой путь, проходящий через все вершины
орграфа. Доказательство: проведем методом математической индукции по числу вершин
орграфа.
Для 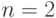 утверждение верно. Теперь предположим, что в любом
полном орграфе
утверждение верно. Теперь предположим, что в любом
полном орграфе  с
с  вершинами найдется простой путь,
проходящий через все вершины графа. Обозначим его
вершинами найдется простой путь,
проходящий через все вершины графа. Обозначим его 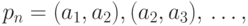
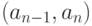 . Добавим теперь произвольную
вершину
. Добавим теперь произвольную
вершину 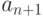 и ребра
(дуги), соединяющие ее со всеми остальными вершинами
орграфа
и ребра
(дуги), соединяющие ее со всеми остальными вершинами
орграфа  .
.
Если ребро (дуга), соединяющее 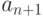 и
и 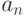 ,
направлено от
,
направлено от 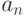 к
к 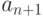 , то пройден путь
, то пройден путь 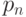 до
до 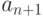 (рис. 10.3).
Если ребро (дуга) направлено от
(рис. 10.3).
Если ребро (дуга) направлено от 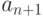 к
к 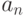 , то
рассмотрим последовательность ребер (дуг), соединяющих
, то
рассмотрим последовательность ребер (дуг), соединяющих 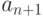 с
с 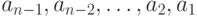 . Если все ребра (дуги) направлены
от
. Если все ребра (дуги) направлены
от 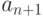 , то к пути
, то к пути  можно добавить ребро
можно добавить ребро 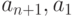 .
.
Если они не все выходят из 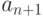 , то возьмем первое ребро
(дугу) этой последовательности, входящее в
, то возьмем первое ребро
(дугу) этой последовательности, входящее в 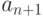 . Пусть это будет ребро
(дуга)
. Пусть это будет ребро
(дуга) 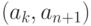 (рис. 10.4).
(рис. 10.4).
Прервем путь 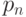 в
в 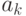 и продолжим его по
ребрам (дугам)
и продолжим его по
ребрам (дугам) 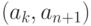 ,
,  , после чего вновь
вернемся к прежнему
маршруту, то есть искомый путь будет следующим:
, после чего вновь
вернемся к прежнему
маршруту, то есть искомый путь будет следующим: 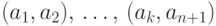 ,
,  ,
, 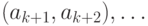 ,
, 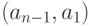
По принципу математической индукции утверждение верно для всякого
натурального  .
.
А коль есть такой путь в графе, следовательно, всех игроков можно будет пронумеровать так, чтобы оказалось, что каждый выиграл партию у шахматиста, имеющего номер на единицу меньше.
Полученный результат сформулируем в виде теоремы.
Теорема 10.2.
Всякий полный орграф с  вершинами имеет простой ориентированный
путь, проходящий через все вершины орграфа.
вершинами имеет простой ориентированный
путь, проходящий через все вершины орграфа.


