|
Здравствуйте! Записался на ваш курс, но не понимаю как произвести оплату. Надо ли писать заявление и, если да, то куда отправлять? как я получу диплом о профессиональной переподготовке? |
Сентенциальное программирование: PROLOG
Рассмотренные до сих пор средства языка PROLOG не дают возможности сформулировать отрицание. Впрочем, отрицание и не может присутствовать в хорновых формулах, его наличие разрушает свойства, которые послужили основой для модели вычислений языка PROLOG. Но на практике оно нужно, и поэтому в языке PROLOG введен его суррогат. Этот суррогат дает возможность программисту минимально управлять точками возврата. Если в цели встал на первое место атом ! (называемый предикатом отсечения ), то он успешно унифицируется и уничтожает последнюю точку возврата. Предикат ! используется прежде всего для определения отрицания как явного неуспеха подцели.
Пример 6.3.2. Рассмотрим, как с помощью ! и списков программируется поиск пути в лабиринте (и даже в произвольном ориентированном графе).
way(X,X,[X]). way(X,Y,[Y|Z]):-connect(U,Y), nomember(Y,Z),way(X,U,Z). way(X,Y,[Y|Z]):-connect(U,Y), way(X,U,Z). nomember(Y,Z):-member(Y,Z),!,fail. nomember(Y,Z). connect(begin,1). connect(1,begin). connect(1,2). connect(2,3). connect(3,1). connect(3,4). connect(4,end).Листинг 6.3.2. Статический лабиринт
?-way(begin,end,X).
X = [end, 4, 3, 2, 1, begin] Yes
Вместо определения nomember можно написать предложение
way(X,Y,[Y|Z]):-connect(U,Y),not (member(Y,Z)),way(X,U,Z).
Предикат отсечения можно использовать для того, чтобы превратить PROLOG -программу в программу с традиционным управлением, оставив из специфики языка лишь операцию унификации. На практике и при обучении часто бывают случаи, когда кому-нибудь никак не удается совладать с PROLOG и отладить свою программу, поскольку он зациклен на императивном стиле программирования. Узнав о !, он облегченно вздыхает и переписывает свою программу таким образом, что она становится изоморфной программе в обычном языке программирования. Как правило, при такой трансформации теряются главные преимущества языка PROLOG, но зато сохраняются все его недостатки.
Внимание!
Некоторые из русскоязычных учебных пособий по языку PROLOG написаны людьми, не понимающими сути других стилей программирования. Видимым признаком такого пособия может служить постоянное использование отсечений.
Прагматические соглашения о порядке выполнения действий в программе привели к тому, что если мы запишем в форме языка PROLOG тривиальную тавтологию
A:-A.
и этот оператор5Здесь мы не оговорились: в данном случае предложения лучше трактовать как операторы, поскольку как утверждения их в данном случае рассматривать невозможно. выполнится, то программа зациклится. И по этой причине, и по причине ошибки в унификации предложения языка PROLOG, сохранив внешнюю форму логических, по существу отношения к логике уже не имеют.
Конечно же, несообразности были использованы и для получения новых эффектов. Рассмотрим следующее определение.
repeat. repeat:-repeat.
Если вставить теперь цель repeat в раскрытие другой цели и позаботиться о том, чтобы последующие подцели в большинстве случаев заканчивались неудачей, а после удачи поставить !, то эти подцели будут повторяться вплоть до удачи и их побочные эффекты будут исполняться в цикле.
Приведенное выше определение repeat писать в программах не нужно. В стандарте PROLOG задан встроенный предикат repeat, потенциально бесконечное число раз успешно унифицируемый. Реализованный в языке PROLOG перебор вариантов при всех своих недостатках довольно удачно моделирует недетерминированные алгоритмы в программе.
Недетерминированную модель вычислений, соответствующую PROLOG, можно определить в общем виде следующим образом:
- Имеются точки разветвления, допускающие переходы без проверки условий выбора вариантов — точки недетерминированного разветвления.
- Вычислительный процесс выбирает в такой точке любое из возможных продолжений.
- Некоторые из возможных продолжений объявляются тупиковыми, или тупиками, т. е. такими, которые не приводят вычислительный процесс к заранее определенной цели. Принципиально, что тупик продолжения не может определиться в точке разветвления.
- Успешным вычислением называется такая последовательность выбираемых продолжений в каждой точке недетерминированного разветвления, которая приводит процесс к цели (т. е. ни одно из выбранных продолжений не является тупиком).
Недетерминированным достижением цели называется успешное вычисление. Таким образом, если какая-то из последовательностей продолжений приводит к цели, то цель процесса считается достигнутой. Недетерминированная модель вычислений может применяться и как средство декомпозиции решаемой задачи, когда программист просто откладывает 'на потом' вопрос, как будет организован перебор вариантов.
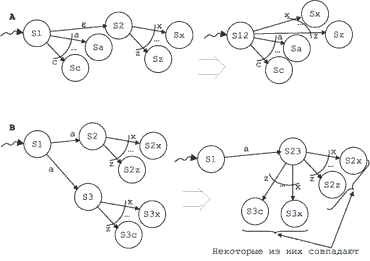
Есть теорема, доказывающая, что в принципе недетерминированный конечный автомат всегда можно преобразовать в детерминированный. Идея преобразования — склейка состояний, как показано на рис. 6.1. При этом, содержательно говоря, мы создаем линейный порядок на множестве альтернатив и выбираем альтернативы в строгом соответствии с этим порядком. Именно так с самого начала поступили в языке PROLOG. Беды в этом нет. В то время, когда создавался язык PROLOG, идея совместности (т. е. безразличия некоторых последовательностей предложений к порядку их исполнения) и недетерминированности (т. е. ситуации, когда один и тот же оператор в одном и том же контексте может давать разные результаты) как положительного фактора была только что осознана. А те, кто делают что-либо принципиально новое, почти всегда забывают согласовать свою находку с другими принципиальными достижениями того же времени, предпочитая локализовать новизну и в остальных пунктах работать как можно более традиционно. Беды начались, когда особенности конкретного упорядочивания стали беспощадно использоваться в хакерском духе, да еще и выставляться как принципиальные новации.
Теорема детерминирования конечного автомата обосновывает существование успешного вычисления. Но она не дает никаких хороших оценок изменения сложности вычислений при переходе к детерминированному поиску. И даже если успешное вычисление существует, это не означает, что трансформировать ассоциированные с переходами действия легко и что после трансформации они будут хоть сколько-нибудь понимаемы. По этой причине часто обработку удобнее описывать как недетерминированную, поручая решение задачи организации перебора вариантов системе программирования.