Сентенциальное программирование: Рефал

Модель вычислений и Рефал-программа

Основные два шага в Рефал -вычислениях — конкретизация переменных в образце в соответствии с областью зрения и подстановка полученных значений в другое метавыражение. В языке рассматривается лишь частный случай конкретизации.

Конкретизация образца Me в объектное выражение E называется такая подстановка значений вместо переменных Me, что после применения данной подстановки Me совпадет с E .

Заметим, что одно и то же метавыражение может иметь много конкретизаций в одно и то же объектное выражение. Например, рассмотрим метавыражение

e.Begin s.Middle e.End                 (5.3)

и объектное выражение

AhAhAh 'OhOhOh' (Ugu','Udgu) '(((' Basta'!'
                                       (5.4)

Имеется 11 вариантов конкретизации (5.3) в (5.4) (проверьте!).

Если у метавыражения Me есть много вариантов конкретизации в E, то они упорядочиваются по предпочтительности в следующем порядке.

Пусть Env1 и Env2 — два варианта конкретизации Me в P. Рассмотрим все вхождения переменных в Me. Если Env1 и Env2 не совпадают, они приписывают некоторым переменным различные значения. Найдем в P самое первое слева вхождение переменной, которому Env1 и Env2 приписывают разные значения и сравним длину этих значений. Та из конкретизаций, в которой значение, приписываемое данному вхождению переменной, короче, предшествует другой и имеет приоритет перед ней.

Например, сопоставим объектное выражение (A1 A2 A3)(B1 B2) с образцом e.1 (e.X s.A e.Y) e.2. В результате получится следующее множество вариантов сопоставления:

{e.1 = ,           eX = ,      sA = A1, eY = A2 A3, e.2 = (B1 B2) }
{e.1 = ,           eX = A1,    sA = A2, eY = A3,    e.2 = (B1 B2) }
{e.1 = ,           eX = A1 A2, sA = A3, eY = ,      e.2 = (B1 B2) }
{e.1 = (A1 A2 A3), eX = ,      sA = B1, eY = B2,    e.2 =         }
{e.1 = (A1 A2 A3), eX = B1,    sA = B2, eY = ,      e.2 =         }

Варианты сопоставления перечислены в соответствии с их приоритетами, т. е. самый первый вариант находится на первом месте и т. д. Описанный способ упорядочения вариантов сопоставления называется сопоставлением слева направо.

Тот алгоритм конкретизации, который используется в Рефале, называется проецированием и согласован с введенным нами отношением порядка. Опишем его (описание взято из учебника Турчина). Обратите внимание, как в данном случае общая и не всегда эффективно реализуемая операция 'проецируется' на свою частную реализацию, одновременно повышающую эффективность, сохраняющую общность и предписывающую методику программирования.

Алгоритм для сопоставления объектного выражения E с образцом P в Рефал-5.

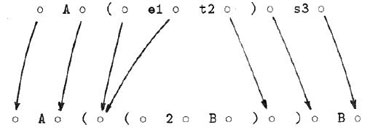
Вхождения атомов, скобок и переменных будут называться элементами выражений. Пропуски между элементами будут называться узлами. Сопоставление E: P определяется как процесс отображения, или проектирования, элементов и узлов образца P на элементы и узлы объектного выражения E. Графическое представление успешного сопоставления приведено на рис. 5.2. Здесь узлы представлены знаками o.

Следующие требования являются инвариантом алгоритма сопоставления и их выполнение обеспечивается на каждой его стадии.

Общие требования к отображению P на E (сопоставлению E : P)

1. Если узел N2 расположен в P правее узла N1, то проекция N2 в E может либо совпадать с проекцией N1, либо располагаться справа от нее (линии проектирования не могут пересекаться).
2. Скобки и атомы должны совпадать со своими проекциями.
   

   
   Рис. 5.2. Сопоставление E : P является отображением P на E. Здесь объектным выражением E является 'A'((2'B'))'B', а образцом P является 'A'(e.1 t.2)s.3
3. Проекции переменных должны удовлетворять синтаксическим требованиям их значений; т. е., быть в соответствии с типом переменной атомами, термами или произвольными выражениями. Различные вхождения одной переменной должны иметь одинаковые проекции.

Предполагается, что в начале сопоставления граничные узлы P отображаются в граничные узлы E. Процесс отображения описывается при помощи следующих шести правил. На каждом шаге отображения правила 1–4 определяют следующий элемент, подлежащий отображению; таким образом, каждый элемент из P получает при отображении уникальный номер.

Правила отображения

1. После того как отображена скобка, следующей подлежит отображению парная ей скобка.
2. Если в результате предыдущих шагов оба конца вхождения некоторой переменной для выражений уже отображены, но эта переменная еще не имеет значения (ни одно другое ее вхождение не было отображено), то эта переменная отображается следующей. Такие вхождения называются закрытыми e-переменными. Две закрытые e-переменные могут появиться одновременно; в этом случае та, что слева, отображается первой.
3. Вхождение переменной, которая уже получила значение, является повторным. Скобки, атомы, символьные и термовые переменные и повторные вхождения переменных для выражений в P являются жесткими элементами. Если один из концов жесткого элемента отображен, проекция второго конца определена однозначно. Если Правила 1 и 2 неприменимы, и имеется несколько жестких элементов с одним спроектированным концом, то из них выбирается самый левый. Если возможно отобразить этот элемент, не вступая в противоречие с общими требованиями 1–3, приведенными выше, тогда он отображается, и процесс продолжается дальше. В противном случае объявляется тупиковая ситуация.
4. Если Правила 1–3 неприменимы и имеются несколько переменных для выражений с отображенным левым концом, то выбирается самая левая из них.Она называется открытой e-переменной. Первоначально она получает пустое значение, т. е. ее правый конец проектируется на тот же узел, что и левый. Другие значения могут присваиваться открытым переменным через удлинение (см. Правило 6).
5. Если все элементы P отображены, это значит, что процесс сопоставления успешно завершен.
6. В тупиковой ситуации процесс возвращается назад к последней открытой e-переменной (т. е. к той, что имеет максимальный номер проекции), и ее значение удлиняется; т. е. проекция ее правого конца в E продвигается на один терм вправо. После этого процесс возобновляется. Если переменную нельзя удлинить (из-за Общих требований 1–3), удлиняется предшествующая открытая переменная, и т. д. Если не имеется подлежащих удлинению открытых переменных, процесс сопоставления не удался.

На рис. 5.2 сопоставление производится следующим образом. Вначале имеется два жестких элемента с одним отображенным концом: 'A' и s.3. В соответствии с Правилом 3 отображается 'A', и этот элемент получает при отображении номер 1.Номера 2 и 3 будут назначены левой и правой скобкам согласно Правилам 3 и 1. Внутри скобок начинается перемещение справа налево, так как t.2 является жестким элементом, который может быть отображен, в то время как значение e.1 еще не может быть определено. На следующем шаге обнаруживается, что e.1 является закрытой переменной, чью проекцию не требуется обозревать для того, чтобы присвоить ей значение; что бы ни было между двумя узлами, это годится для присвоения (на самом деле, значение e.1 оказывается пустым). Отображение s.3 завершает сопоставление. Расположение отображающих номеров над элементами образца дает наглядное представление описанного алгоритма:

1  2  5   4  3  6
'A' ( e.1 t.2 ) s.3

Этот сложный алгоритм упрятан в простые программные конструкции.

Программа на Рефале является последовательностью определений функций. Каждое описание функции в Рефале имеет вид

Имя функции {Последовательность сопоставлений}

Каждое сопоставление имеет вид

Образец = Метавыражение;

Относительное расположение членов последовательности определений никакой роли не играет, и функции можно группировать из логических или технологических соображений. Относительное расположение сопоставлений внутри определения функции существенно.

Пример 5.3.2. Рассмотрим пример Рефал -программы.

Pre_alph {
*1. Отношение рефлексивно
    s.1 s.1 = T;
*2. Если буквы различны, проверить, входит ли
* первая из них в алфавит до второй
    s.1 s.2 = <Before s.1 s.2 In <Alphabet>>; }
Before {
    s.1 s.2 In e.A s.1 e.B s.2 e.C = T;
    e.Z = F; }
Alphabet {
    = 'abcdefghijklmnopqrstuvwxyz'; }

Строки, начинающиеся с *, служат комментариями. Последняя из функций Alphabet введена для технологичности, чтобы определение алфавита было в одном месте и его легко было изменять. Так что функция с пустым образцом может пониматься как константное выражение. In является атомом-разделителем, заведомо не встречающимся в алфавите.

Последнее из правил сопоставления в Before применимо всегда. Такое сопоставление гарантирует, что предикат никогда не заканчивается неудачей.

Если взаимное расположение функций никакой роли не играет, то внутри функции расположение сопоставлений важно. Сначала применяется первое из сопоставлений, при неудаче переходят ко второму и так далее до последнего.

Заметим, что в языке Рефал отсутствие сопоставления, конкретизацией которого является текущая область зрения, означает аварийный останов программы с выдачей текущего поля памяти и закопанных данных. Пожалуй, это достаточно технологичное решение, поскольку для тех, кто сам желает обрабатывать ошибки, всегда имеется возможность поместить последней строкой в определение функции правило вида e.A=Обработка ошибки ;

Имеются также встроенные функции, в частности, функции работы с числами <'+' s.Number1 s.Number2> и подобные ей.

Рассмотрим связь между языком и программным окружением.

Для запуска Рефал -программы необходимо инициализировать поле памяти. Принято, что в начале выполнения программы поля памяти имеет вид

<Go >

Таким образом, вначале применяется функция Go к пустому полю зрения. Эта функция должна быть определена в программе одним сопоставлением с пустым образцом и не может вызываться никакой другой функцией. Поскольку чаще всего программа должна обрабатывать имеющиеся в файле исходные данные, в типичном случае описание функции Go выглядит примерно следующим образом:

$ENTRY Go { =<Prog <Open 'r' 1 'data.txt'><Get 1> >}