Визуализация пространственных реалистических сцен
Метод излучательности
В этой лекции уже говорилось, что освещенность поверхности определяется собственным излучением тела и отраженными лучами, падающими от других тел (источников). Модель излучательности включает оба эти фактора и основана на уравнениях энергетического баланса. При этом выполняемые расчеты учитывают только взаимное расположение элементов сцены и не зависят от положения наблюдателя.
Представим сцену из  элементов (участков поверхностей).
Освещенность будем моделировать как количество энергии, излучаемое
поверхностью. Для каждого элемента это количество энергии складывается
из собственной энергии
элементов (участков поверхностей).
Освещенность будем моделировать как количество энергии, излучаемое
поверхностью. Для каждого элемента это количество энергии складывается
из собственной энергии 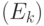 и отраженной доли энергии, полученной от
других объектов. Предполагается, что для каждой пары элементов с
номерами
и отраженной доли энергии, полученной от
других объектов. Предполагается, что для каждой пары элементов с
номерами  можно определить, какая доля энергии одного попадает на
другой
можно определить, какая доля энергии одного попадает на
другой 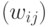 . Пусть
. Пусть 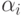 - коэффициент отражения энергии
- коэффициент отражения энергии 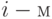 элементом.
Тогда полная энергия, излучаемая этим элементом, будет определяться
уравнением
элементом.
Тогда полная энергия, излучаемая этим элементом, будет определяться
уравнением 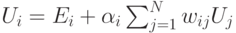 .
.
Таким образом, мы получаем систему уравнений для нахождения
значений 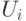 , которая в матричном виде выглядит следующим образом:
, которая в матричном виде выглядит следующим образом:
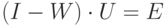
 - единичная матрица,
- единичная матрица,  и
и  - векторы излучаемой и собственной
энергий, а матрица
- векторы излучаемой и собственной
энергий, а матрица  состоит из элементов
состоит из элементов 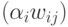 . Поскольку часть излучения
элемента может не попадать ни на один из оставшихся, то
. Поскольку часть излучения
элемента может не попадать ни на один из оставшихся, то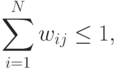
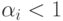 (отражение не является полным),
приводит к тому, что матрица системы имеет так называемое диагональное
преобладание, т.е. диагональный элемент по абсолютной величине
больше, чем сумма остальных элементов строки. В таком случае система
уравнений имеет решение, которое можно найти с помощью численных
методов.
(отражение не является полным),
приводит к тому, что матрица системы имеет так называемое диагональное
преобладание, т.е. диагональный элемент по абсолютной величине
больше, чем сумма остальных элементов строки. В таком случае система
уравнений имеет решение, которое можно найти с помощью численных
методов.Итак, шаги алгоритма изображения сцены сводятся к следующим:
- Сцена разбивается на отдельные участки, для каждого из которых определяются значения
 .
. - Находятся значения
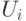 для каждой из трех основных компонент цвета.
для каждой из трех основных компонент цвета. - Для выбранной точки наблюдения строится проекция с удалением невидимых граней и осуществляется закрашивание, использующее значения
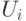 для задания интенсивности. При этом могут использоваться какие-либо алгоритмы, позволяющие сгладить изображение.
для задания интенсивности. При этом могут использоваться какие-либо алгоритмы, позволяющие сгладить изображение.
Сложным моментом в модели излучательности является расчет коэффициентов 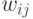 .
.
Рассмотрим один пример. Пусть имеется два элемента сцены  и
и  (рис. 10.2). Поскольку используется диффузная модель освещения, то
доля энергии малого участка
(рис. 10.2). Поскольку используется диффузная модель освещения, то
доля энергии малого участка  с нормалью
с нормалью  , излучаемая под углом
, излучаемая под углом 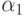 к
этой нормали, пропорциональна косинусу угла. Следовательно, в
направлении элементарного участка
к
этой нормали, пропорциональна косинусу угла. Следовательно, в
направлении элементарного участка  уходит доля энергии,
пропорциональная косинусу угла между
уходит доля энергии,
пропорциональная косинусу угла между  и отрезком, который соединяет
эти участки. Соответственно, получаемая вторым участком доля этой
энергии будет пропорциональна косинусу угла между нормалью
и отрезком, который соединяет
эти участки. Соответственно, получаемая вторым участком доля этой
энергии будет пропорциональна косинусу угла между нормалью 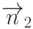 и этим же
отрезком. Итак, доля энергии, получаемая элементом
и этим же
отрезком. Итак, доля энергии, получаемая элементом  от элемента ,
от элемента ,  -
- 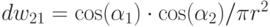 , где
, где  - расстояние между элементами. Кроме того, необходимо учесть,
что излучаемая элементарным участком энергия равномерно распределена
по всем направлениям. И, наконец, в каждой сцене одни объекты могут
частично экранировать другие, поэтому надо ввести коэффициент,
определяющий степень видимости объекта с позиции другого. Далее
полученное выражение интегрируется по
- расстояние между элементами. Кроме того, необходимо учесть,
что излучаемая элементарным участком энергия равномерно распределена
по всем направлениям. И, наконец, в каждой сцене одни объекты могут
частично экранировать другие, поэтому надо ввести коэффициент,
определяющий степень видимости объекта с позиции другого. Далее
полученное выражение интегрируется по  и
и 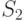 , что также может быть
сложной задачей.
, что также может быть
сложной задачей.
Отсюда видно, насколько трудоемкой может оказаться процедура
вычисления коэффициентов 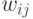 . Поэтому, как правило, используются
приближенные методы их вычисления. В частности, можно рассматривать
поверхности объектов как многогранники, тогда элементами сцены будут
плоские многоугольники, для которых формулы несколько упрощаются.
. Поэтому, как правило, используются
приближенные методы их вычисления. В частности, можно рассматривать
поверхности объектов как многогранники, тогда элементами сцены будут
плоские многоугольники, для которых формулы несколько упрощаются.


