|
Подскажите, пожалуйста, планируете ли вы возобновление программ высшего образования? Если да, есть ли какие-то примерные сроки? Спасибо! |
Статистическое моделирование
3.12. Модель противоборства двух сторон
Имитационную модель, в которой продвижение модельного времени реализовано с фиксированным шагом, рассмотрим на примере огневого противоборства группировок A и В. Аналитическое моделирование такой операции мы рассмотрели в предыдущей теме. Однако мы снимаем условие многочисленности группировок, так как оно теперь несущественно.
Для начала, чтобы не загромождать алгоритм модели, введем два ограничения:
- вероятность поражения цели одним выстрелом
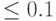 ;
; - вероятность одновременного поражения двумя средствами друг друга пренебрежимо мала.
Впоследствии мы убедимся, что в имитационной модели рассматриваемого боя эти ограничения могут быть сняты.
Моделирование проводится с целью определения средних численностей группировок на любой момент боя, в частности, на фиксированный момент времени 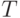 .
.
Учебная задача состоит в том, чтобы изучить структуру конкретного алгоритма, в котором продвижение модельного времени реализовано с фиксированным шагом  .
.
Введем обозначения:
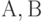 - первоначальные численности группировок;
- первоначальные численности группировок;
 - текущие значения численностей группировок
- текущие значения численностей группировок  и
и 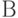 соответственно;
соответственно;
 - число оставшихся средств каждой из сторон в конце
- число оставшихся средств каждой из сторон в конце  -го интервала моделирования (после
-го интервала моделирования (после  -ой реализации модели);
-ой реализации модели);
 - текущее число реализаций модели;
- текущее число реализаций модели;
 - заданное число реализаций модели случайного процесса;
- заданное число реализаций модели случайного процесса;
 - длительность интервала моделирования;
- длительность интервала моделирования;
 - средние за
- средние за  реализаций модели численности оставшихся средств сторон в конце каждого интервала моделирования:
реализаций модели численности оставшихся средств сторон в конце каждого интервала моделирования:
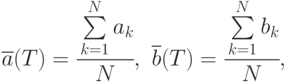
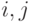 - переменные счета средств сторон
- переменные счета средств сторон  и
и 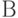 соответственно .
соответственно .
Идея построения имитационной модели состоит в реализации модели противоборства  раз и фиксации остатков сторон после каждой реализации. По выполнении
раз и фиксации остатков сторон после каждой реализации. По выполнении  реализаций будут определены оценки численностей сторон
реализаций будут определены оценки численностей сторон  .
.
Определим величину  . На выбор величины
. На выбор величины  влияют два противоречивых требования:
влияют два противоречивых требования:
- на протяжении отрезка времени
 не должно происходить много событий, так как они будут зафиксированы как одновременные, что исказит исследуемый реальный процесс;
не должно происходить много событий, так как они будут зафиксированы как одновременные, что исказит исследуемый реальный процесс; - на протяжении отрезка времени
 должно произойти хотя бы одно событие, иначе будет много "пустых" прогонов модели, что увеличит машинное время.
должно произойти хотя бы одно событие, иначе будет много "пустых" прогонов модели, что увеличит машинное время.
С учетом приведенных выше требований разобьем интервал моделирования 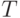 на равные отрезки
на равные отрезки  такие, чтобы каждое огневое средство любой из сторон могло выстрелить не более одного раза.
такие, чтобы каждое огневое средство любой из сторон могло выстрелить не более одного раза.
Например, скорострельность средств поражения стороны 
 , а средств стороны
, а средств стороны 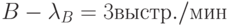 . Так как
. Так как  , то
, то  следует выбрать исходя из условия
следует выбрать исходя из условия 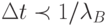 .
.
Алгоритм имитации противоборства сторон состоит из четырех модулей:
-
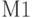 - установка начальных условий;
- установка начальных условий; -
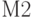 - продвижение модельного времени;
- продвижение модельного времени; -
 - формирование результата заданной точности;
- формирование результата заданной точности; -
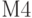 - имитация противоборства сторон.
- имитация противоборства сторон.
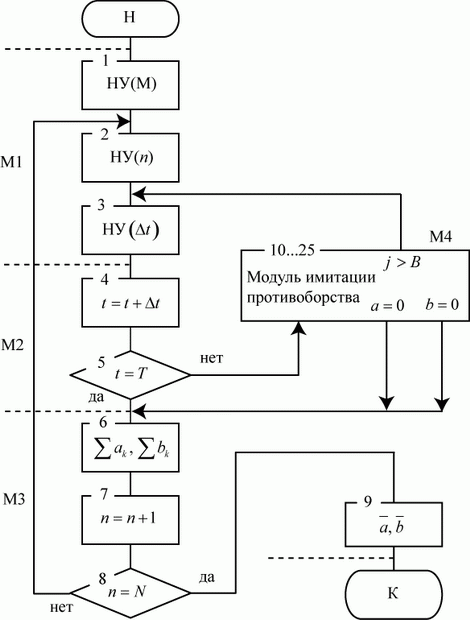
Блок-схема алгоритма имитации противоборства двух сторон показана на рис. 3.23.
Модуль установки начальных условий ( 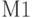 ). Он состоит из трех блоков 1… 3.
). Он состоит из трех блоков 1… 3.
Блок 1 - установка начальных условий на весь процесс моделирования: число реализаций  модели, интервал исследования
модели, интервал исследования  , величина временного шага
, величина временного шага  , установка в нуль ячеек
, установка в нуль ячеек 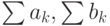
Блок 2 - установка начальных условий на очередную реализацию процесса: восстановление численностей сторон 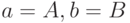 и исходного времени
и исходного времени 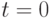 .
.
Блок 3 - установка начальных условий на очередной отрезок  модельного времени: подготовка перебора
модельного времени: подготовка перебора 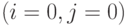 средств
средств
поражения каждой стороны.
Модуль продвижения модельного времени (  ). Состоит из двух блоков 4..5.
). Состоит из двух блоков 4..5.
Блок 4 - продвижение модельного времени на очередной временной отрезок 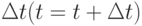 .
.
Блок 5 - проверка условия окончания очередной реализации модели  .
.
Модуль формирования результата и обеспечения заданной точности (  ). Состоит из блоков 6…9.
). Состоит из блоков 6…9.
Блок 6 - накопление суммы остатков средств каждой стороны за текущее количество интервалов моделирования (реализаций модели).
Блок 7 - счетчик числа реализаций модели ( 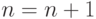 ) .
) .
Блок 8 - осуществляет контроль над выполнением заданного числа реализаций модели. Число реализаций модели определяется, исходя из заданных точности и достоверности результатов моделирования.
Блок 9 - формирование конечного результата моделирования.
В данном случае -  и
и  .
.
При необходимости определяются и другие статистические характеристики.
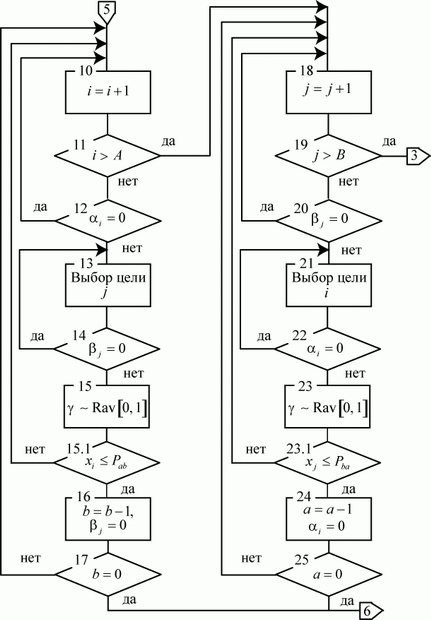
Модуль имитации противоборства сторон ( 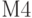 ). Этот модуль - основной. Если структура предыдущих модулей, в общем-то, стандартна, то реализация данного модуля носит функционально-индивидуальный характер. Модуль включает блоки 10…25. Блок-схема алгоритма модуля представлена на рис. 3.24.
). Этот модуль - основной. Если структура предыдущих модулей, в общем-то, стандартна, то реализация данного модуля носит функционально-индивидуальный характер. Модуль включает блоки 10…25. Блок-схема алгоритма модуля представлена на рис. 3.24.
Каждое средство противоборствующих сторон идентифицируется его номером. Номера средств стороны  -
- 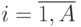 , средств стороны
, средств стороны 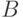 -
- 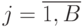 .
.
Блок 10 - выбор очередного средства стороны  :
: 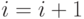 .
.
Блок 11 - проверка: все ли средства стороны  получили право на выстрел? Если
получили право на выстрел? Если  , то управление передается блоку 18 для имитации выстрелов средствами стороны
, то управление передается блоку 18 для имитации выстрелов средствами стороны  . В противном случае управление передается блоку 12.
. В противном случае управление передается блоку 12.
Блок 12 - проверка: боеспособно ли выбранное средство? Состояние средств сторон  и
и 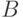 определяют переменные
определяют переменные  и
и 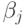 :
:

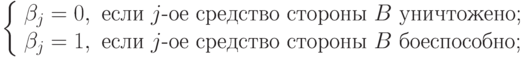
Если окажется 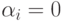 , то управление передается блоку 10 для
, то управление передается блоку 10 для
выбора очередного средства стороны  . Иначе - переход к блоку 13.
. Иначе - переход к блоку 13.
Блок 13 - выбор цели из средств стороны 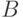 . Выбор цели может быть организован либо случайной, либо детерминированной процедурами. Самый простой способ: последовательная проверка средств стороны
. Выбор цели может быть организован либо случайной, либо детерминированной процедурами. Самый простой способ: последовательная проверка средств стороны 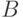 с выбором первого непораженного средства.
с выбором первого непораженного средства.
Блок 14 - проверка выбранной цели: не уничтожена ли она была на предыдущих этапах данной реализации модели? Если  , то переход к блоку 13 для выбора непораженной цели.
, то переход к блоку 13 для выбора непораженной цели.
Иначе - переход к блоку 15 для имитации выстрела.
Выстрел - одиночное событие со случайным исходом. Моделью такого события является известная нам конструкция из двух блоков 15 и 15.1.
Блок 15 - обращение к ДСЧ за равномерно распределенным случайным числом ![х_i \sim Rav[0, 1]](/sites/default/files/tex_cache/d90828c7e23d7e93dc4201d0882cbce9.png) .
.
Блок 15.1 - проверка результата выстрела. Если  , цель поражена и управление передается блоку 16 для фиксации этого факта. Если
, цель поражена и управление передается блоку 16 для фиксации этого факта. Если  , то промах и управление передается блоку 10 для выбора очередного стреляющего средства стороны
, то промах и управление передается блоку 10 для выбора очередного стреляющего средства стороны  .
.
Блок 16 - уменьшение числа средств стороны  :
: 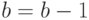 и установка признака состояния пораженного средства:
и установка признака состояния пораженного средства:  .
.
Блок 17 - не уничтожена ли вся группировка 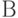 ? Если да, то данная реализация модели заканчивается и управление передается блоку 6 для фиксации оставшихся боеспособных средств стороны
? Если да, то данная реализация модели заканчивается и управление передается блоку 6 для фиксации оставшихся боеспособных средств стороны  . Если нет, то управление передается блоку 10 для выбора очередного средства стороны
. Если нет, то управление передается блоку 10 для выбора очередного средства стороны  и т. д.
и т. д.
После предоставления права на выстрел всем средствам стороны  соответствующее право дается средствам стороны
соответствующее право дается средствам стороны  - переход из блока 11 в блок 18.
- переход из блока 11 в блок 18.
Функции блоков 18… 25 попарно одинаковы с функциями блоков 10…17, изменены только обозначения - вместо  указано
указано  , вместо
, вместо 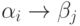 , вместо
, вместо  и т. д.
и т. д.
По окончании перебора всех средств стороны  и, если не зафиксировано полное уничтожение средств стороны
и, если не зафиксировано полное уничтожение средств стороны  , управление передается блоку 3 для моделирования очередного скачка времени на величину
, управление передается блоку 3 для моделирования очередного скачка времени на величину  .
.
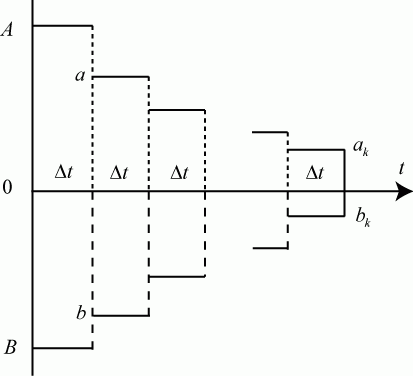
Примерная диаграмма изменения численностей сторон  и
и  в
в  -й реализации на интервале
-й реализации на интервале 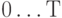 показана на рис. 3.25.
показана на рис. 3.25.

 -
-