|
Здравствуйте! Записался на ваш курс, но не понимаю как произвести оплату. Надо ли писать заявление и, если да, то куда отправлять? как я получу диплом о профессиональной переподготовке? |
Функциональное программирование
Функциональное программирование объясняется на примере диалекта Common Lisp языка LISP. Этот диалект наиболее распространен и имеет официальный стандарт. Common Lisp может работать не только в пакетном режиме (когда он запускается как обычная программа), но и в режиме диалога.
LISP — вероятно, первый из практически реализованных языков1И уж точно первый из выживших, поскольку Plankalk  l Цузе умер вместе с его машинами.
, который основывался на серьезном теоретическом фундаменте и пытался поднять практику программирования до уровня концепций, а не наоборот — опустить концепции до уровня существовавшей на момент создания языка практики.
l Цузе умер вместе с его машинами.
, который основывался на серьезном теоретическом фундаменте и пытался поднять практику программирования до уровня концепций, а не наоборот — опустить концепции до уровня существовавшей на момент создания языка практики.
В настоящий момент функциональное программирование представлено целым семейством языков, но LISP свои позиции не сдает.
Лямбда-абстракции
В некоторых случаях осознанное усвоение концепций даже на самом низком уровне нереально без базовых теоретических сведений. А знакомство с таким базисом, в свою очередь, стимулирует значительно более глубокий интерес к теории и способствует пониманию того, что на высшие уровни знаний и умений не подняться без овладения теорией.
Теоретической основой языка LISP является логика функциональности: комбинаторная логика или (по наименованию одного из основных понятий в наиболее популярной из нынешних ее формализаций)  -исчисление.
-исчисление.
В  -исчислении выразительные средства, на первый взгляд, крайне скупы. Имеются две базисные операции: применение функции к аргументу (fx) и квантор образования функции по выражению
-исчислении выразительные средства, на первый взгляд, крайне скупы. Имеются две базисные операции: применение функции к аргументу (fx) и квантор образования функции по выражению ![\lambda x t[x]](/sites/default/files/tex_cache/ddc4d498d3fb60869bd3935e7f13d438.png) . В терминах
. В терминах  -исчисления функция возведения числа в квадрат записывается как
-исчисления функция возведения числа в квадрат записывается как  или, если быть ближе к обычным математическим обозначениям,
или, если быть ближе к обычным математическим обозначениям,  .
.
Основная операция — символьное вычисление применения функции к аргументу: ![(\lambda x t[x] u)](/sites/default/files/tex_cache/7af0395e238d8a929bac00828504c8fb.png) преобразуется в t[u]. Но эта операция может применяться в любом месте выражения, так что никакая конкретная дисциплина вычислений не фиксируется. Более того, функции могут вычисляться точно так же, как аргументы. Уже эта маленькая тонкость приводит к принципиальному расширению возможностей
преобразуется в t[u]. Но эта операция может применяться в любом месте выражения, так что никакая конкретная дисциплина вычислений не фиксируется. Более того, функции могут вычисляться точно так же, как аргументы. Уже эта маленькая тонкость приводит к принципиальному расширению возможностей  -исчисления по сравнению с обычными вызовами процедур. Если мы желаем ограничиться лишь ею, рассматривается типизированное
-исчисления по сравнению с обычными вызовами процедур. Если мы желаем ограничиться лишь ею, рассматривается типизированное  -исчисление, в котором, как принято в большинстве современных систем программирования, значения строго разделены по типам. В типизированном
-исчисление, в котором, как принято в большинстве современных систем программирования, значения строго разделены по типам. В типизированном  -исчислении есть только типы функций, но этого хватает, поскольку функции могут принимать в качестве параметров и выдавать функции.
-исчислении есть только типы функций, но этого хватает, поскольку функции могут принимать в качестве параметров и выдавать функции.
Но в исходной своей форме  -исчисление является нетипизированным, любой объект может быть и функцией, и аргументом, и, более того, функция может применяться к самой себе. Конечно же, при этом появляется возможность зацикливания, но без нее не обойдется ни одна "универсальная" алгоритмическая система. Например, выражение
-исчисление является нетипизированным, любой объект может быть и функцией, и аргументом, и, более того, функция может применяться к самой себе. Конечно же, при этом появляется возможность зацикливания, но без нее не обойдется ни одна "универсальная" алгоритмическая система. Например, выражение

вычисляется бесконечно, а чуть более сложное выражение
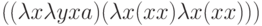
может либо дать a, либо зациклиться, в зависимости от выбора порядка его вычисления. Но все равно, если мы приходим к результату, то он определяется однозначно. Так что совместность вычислений не портит однозначности, если язык хорошо сконструирован.
Дж. Маккарти перенес идеи  -исчисления в программирование, не потеряв практически ничего из исходных концепций. Далее, он заметил, что в рудиментарном виде в
-исчисления в программирование, не потеряв практически ничего из исходных концепций. Далее, он заметил, что в рудиментарном виде в  -исчислении появилось понятие списка, и перенес списки в качестве основных структур данных в свой язык.
-исчислении появилось понятие списка, и перенес списки в качестве основных структур данных в свой язык.  -исчислением было навеяно и соглашение языка LISP о том, что первый член списка трактуется как функция, применяемая к остальным.
-исчислением было навеяно и соглашение языка LISP о том, что первый член списка трактуется как функция, применяемая к остальным.
Списки и функциональные выражения
Основной единицей данных для LISP -системы является список.
Списки задаются следующим индуктивным определением.
- Пустой список () (обозначаемый также nil ) является списком.
- Если l1,. . . , ln, n >= 1 — атомы либо списки, то (l1, . . . , ln) — также список.
Элементами списка (l1, . . . , ln) называются l1, . . . , ln. Равенство списков задается следующим индуктивным определением.
- l = nil тогда и только тогда, когда l также есть nil.
- (l1, . . . , ln) = (k1, . . . , km) тогда и только тогда, когда n = m и соответствующие li = ki.
Пример 8.2.2. Все списки (), (()), ((())) и т. д. различны. Различны также и списки nil, (nil, nil), (nil, nil, nil) и так далее. Попарно различны и списки ((A,B), C), (A, (B,C)), (A,B,C), где A, B, C — различные атомы.
Поскольку понятие, задаваемое индуктивным определением, должно строиться в результате конечного числа шагов применения определения, мы исключаем списки, ссылающиеся сами на себя. Списки в нашем рассмотрении изоморфны упорядоченным конечным деревьям, листьями которых являются nil либо атомы.
Вершины списка L задаются следующим индуктивным определением.
Длиной списка называется количество элементов в нем. Глубиной списка называется максимальное количество вложенных пар скобок в нем. Соединением списков (l1, . . . , ln) и (k1, . . . , km) называется список
(l1, . . . , ln, k1, . . . , km).
Замена вершины a списка L на атом либо список M получается заменой поддерева L, соответствующего a, на дерево для M. Замена обозначается L[a | M]. Через L[a || M] будем обозначать результат замены нескольких вхождений вершины a на M.
Атомами в языке LISP являются числа, имена, истина T. Ложью служит пустой список NIL, который в принципе атомом не является, но в языке LISP при проверке на то, является ли он атомом, выдается истина. Точно так же выдается истина и при проверке, является ли он списком. Однако все списковые операции применимы к NIL, а те, которые работают с атомами, часто к нему неприменимы. Например, попытка присваивания значения выдает ошибку.
Основная операция для задания списков (list a b . . . z). Она вычисляет свои аргументы и собирает их в список. Для этой операции без вычисления аргументов есть скоропись ’(a b . . . z). Она является частным случаем функции quote (сокращенно обозначаемой ’ ), которая запрещает всякие вычисления в своем аргументе и копирует его в результат так, как он есть.
По традиции, элементарные операции разбора списков обозначаются именами, которые начинаются с c и кончаются на r, а в середине идет некоторая последовательность букв a и d ; (car s) выделяет голову (первый член списка ), (cdr s) — хвост (подсписок всех членов, начиная со второго). Буквы a и d применяются, начиная с конца. Общее число символов в получающемся атоме должно быть не больше шести. Рассмотрим фрагмент диалога, иллюстрирующий эти операции. Как только в диалоге вводится законченное выражение, оно вычисляется либо выдается ошибка.
[13]>(setq a ’(b c (d e) f g)) (B C (D E) F G) [14]> (cddr a) ((D E) F G) [15]> (cddar a) *** - CDDAR: B is not a list 1. Break [16]> ^Z [17]> (caaddr a) D [18]> (cdaddr a) (E)
Поле зрения и поле памяти
Если не применены специальные операции блокирования вычислений, первый аргумент списка интерпретируется как функция, аргументами которой являются оставшиеся элементы списка. Это позволяет программу также задавать списком.
Таким образом, в LISP, так же, как в сентенциальных языках, структура данных программы и поля памяти, обрабатываемого программой, совпадают. Видимо, это одна из удачнейших форм поддержания концептуального единства для высокоуровневых систем.
В поле памяти с каждым атомом-именем могут быть связаны атрибуты. Стандартный атрибут — значение атома. Для установки этого атрибута есть функция (setq atom value), аналогичная присваиванию. Эта функция не вычисляет свой первый аргумент, она рассматривает его как имя, которому нужно приписать значение.
Значение в языке LISP может быть локальным. Если мы изменили значение атома внутри некоторого блока, то такое ‘присваивание’ действует лишь внутри минимальных объемлющих его скобок и исчезает снаружи блока. Кроме значения, имена могут иметь сколько угодно других атрибутов, которые обязательно глобальны. Они принадлежат самому имени, а не блоку. Способ установки значений этих атрибутов несколько искусственный. Имеется еще одна функция setf, вычисляющая свой первый аргумент, дающий ссылку на место, которому можно приписать значение (например, на атрибут ). Функция получения значения атрибута get, даже если атрибута еще нет, указывает на его место. Следующий пример демонстрирует, как это работает.
[38]> (setf (get ’b ’weight) ’(125 kg)) (125 KG) [39]> (get ’b ’weight) (125 KG)
Рассмотрим подробнее структуру данных языка LISP. Она является двухуровневой. На верхнем уровне имеется структура списков. На нижнем находится структура информации, сопоставленной атому. Она изображена на рис. 8.1. Оба этих уровня рекурсивно ссылаются друг на друга, например, атрибуты атома являются списками.
Типы данных (в смысле программирования) в LISP есть, но они определяются динамически. В частности, если действительное число придано атому как значение, то тип атома становится float.
