Тупики (deadlocks), методы предотвращения и обнаружения тупиков
Поиск тупиков по графу распределения ресурсов
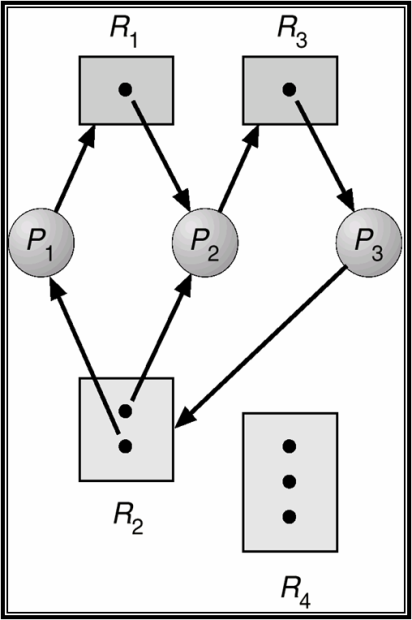
Очевидно, что цикл в таком графе может означать наличие тупика. На рис. 13.4 приведен пример графа с тупиком. Имеется ситуация циклического ожидания между процессами 1, 2 и 3. Процесс 1 претендует на ресурс, которым владеет процесс 2. Процесс 2 претендует на ресурс, которым владеет процесс 3. Процесс 3 претендует на ресурс, одна единица которого отдана процессу 1, а вторая – процессу 2.
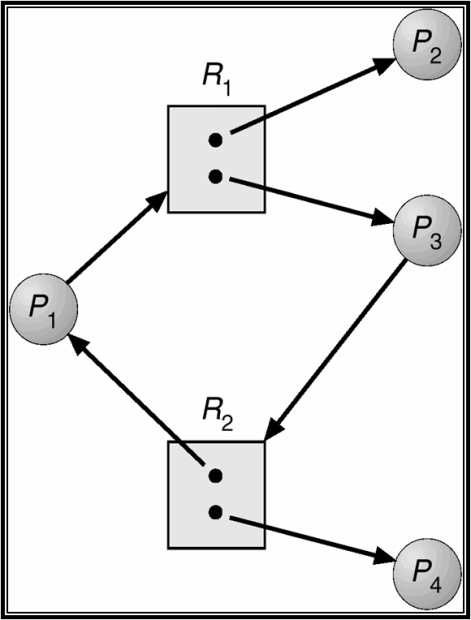
Однако не всегда наличие цикла в графе распределения ресурсов означает наличие тупика. На рис. 13.5 приведен пример графа распределения ресурсов с циклом, но без тупика.
В данном случае ( рис. 13.5) имеется четыре процесса и два вида ресурсов. В цикле участвуют вершины-процессы 1 и 3. Однако, благодаря тому, что каждого ресурса имеется по две единицы, тупика удается избежать: процесс 1, ожидающий ресурса 1, сможет его получить, когда завершится процесс 2 (а не процесс 1), обладающий одной единицей данного ресурса и не входящий в цикл ожидания. Аналогично, процесс 3, претендующий на ресурс 2, сможет его получить после его освобождения процессом 4 (а не 1).
Таким образом, можно сформулировать следующие утверждения:
- Если граф распределения ресурсов не содержит циклов, то в системе тупиков нет;
- Если граф распределения ресурсов содержит цикл, то возможно два случая:
Методы обработки тупиков
Теоретически возможны следующие методы обработки тупиков:
- Убедиться в том, что система никогда не войдет в состояние тупика;
- Допустить, чтобы система могла входить в состояние тупика, но предусмотреть возможность восстановления после тупика.
К сожалению, на практике во многих ОС (включая UNIX) используется и третий "метод" борьбы с тупиками: проблема тупиков игнорируется, но авторы ОС без каких-либо обоснований претендуют на то, что в системе тупики невозможны.
Предотвращение тупиков
Проанализируем, какие методы предотвращения тупиков возможны. Основная идея – ограничить методы запросов ресурсов со стороны процессов.
Чтобы ограничить возможность взаимного исключения владения ресурсами (первое условие тупика), необходимо заметить, что оно требуется не для всех ресурсов. Для разделяемых ресурсов (например, массивов констант, кодов, файлов) оно не требуется.
Чтобы ограничить возможность удержания и ожидания (второе условие тупика), можно потребовать, чтобы процесс, запрашивающий некоторый ресурс, не обладал бы больше никакими ресурсами. Альтернативным вариантом является требование, чтобы все процессы приобретали все необходимые им ресурсы до фактического начала их исполнения. К сожалению, реализация обоих этих требований приводит к недостаточности использования ресурсов и возможности "голодания" (starvation).
Более разумной представляется стратегия перераспределения ресурсов при каждом ожидании процессом ресурса. Если процесс обладает некоторым ресурсом A и запрашивает другой ресурс B, который не может быть ему немедленно выделен, то процесс должен ждать. При этом ресурс A,занимаемый процессом, должен быть немедленно освобожден.Ресурс A добавляется к списку ресурсов, которые ожидает процесс. Процесс может быть возобновлен, только если ему могут быть выделены одновременно все старые ресурсы, которыми он обладал, и те новые ресурсы, которых он ожидает.
Для предотвращения ситуации циклического ожидания самое простое решение – ввести упорядочение по номерам всех видов ресурсов и требовать, чтобы процесс запрашивал ресурсы только в порядке возрастания их номеров. На практике подобное решение вряд ли применимо и удобно, так как специфика потребляемых и требуемых типов ресурсов никак не зависит ни от какой возможной нумерации, и потребность в ресурсе с любым номером может возникнуть по мере необходимости.
Избежание тупиков
Методы избежания тупиков требуют, чтобы система обладала дополнительной априорной информацией о процессе и его потребностях в ресурсах с момента ввода каждого процесса в систему.
Наиболее простая и полезная модель требует, чтобы каждый процесс при вводе в систему указывал максимальный объем ресурсов каждого типа, которые могут ему понадобиться. Данный подход был реализован даже в ранних ОС и носит название паспорт задачи – список максимальных потребностей процесса в ресурсах каждого типа – оперативной и внешней памяти, времени выполнения, листах печати и др.
Например, в ОС ДИСПАК для БЭСМ-6 (еще в 1960-х гг.) паспорт задания мог иметь вид:
ЛИСТ 0-37^ТРАК 50^ВРЕМ 240^АЦПУ 10^
где ЛИСТ – диапазон листов (страниц) основной памяти, ТРАК – требуемый объем внешней памяти на магнитном барабане, ВРЕМ – максимальное время выполнения (2 минуты 40 секунд, что соответствовало одному из быстрых классов заданий), АЦПУ – максимальный объем выдачи на печатающее устройство в листах.
При попытке превышения хотя бы одного из указанных ограничений операционная система снимала задачу со счета с соответствующим диагностическим сообщением для пользователя.
Вернемся к избежанию тупиков. Алгоритм избежания тупиков должен анализировать состояние распределения ресурсов, чтобы убедиться, что никогда не может возникнуть ситуация циклического ожидания.
Состояние распределения ресурсов описывается как объем доступных ресурсов, объем распределенных ресурсов и максимальные требования процессов.
В следующей лекции рассмотрены конкретные методы и алгоритмы избежания тупиков и определения безопасности состояния системы, основанные на данных принципах.