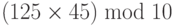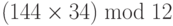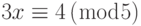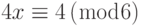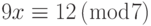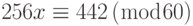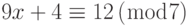|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Сравнения и матрицы
3.3. Рекомендованная литература
Для более детального изучения положений, обсужденных в этой лекции, мы рекомендуем нижеследующие книги и сайты. Пункты, указанные в скобках, показаны в списке ссылок в конце книги.
Книги
Несколько книг дают простой, но полный охват теории чисел: [Ros06], [Sch99], [Cou99] и [BW00]. Матрицы обсуждаются в любой книге по линейной алгебре: [LEF04], [DF04] и [Dur05] — это хорошие книги для начинающих.
Сайты
Нижеследующие сайты дают больше информации о темах, рассмотренных в этой лекции.
- http:en.wikipedia.org/wiki/Euclidean_algorithm
- http:en.wikipedia.org/wiki/Multiplicative_inverse
- http:en.wikipedia.org/wiki/Additive-inverse
3.4. Итоги
- Множество целых чисел, обозначаемое Z, содержит все целые числа от отрицательной бесконечности до положительной бесконечности. Для целых чисел определены три общих бинарных операции — сложение, вычитание и умножение. Деление не удовлетворяет определению бинарности, потому что требует два выхода вместо одного.
- В арифметике целых чисел, если мы делим a на n, мы можем получить q и r. Отношение между этими четырьмя целыми числами можно показать как
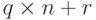 . Мы говорим a|n, если
. Мы говорим a|n, если 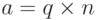 . В этой лекции мы рассмотрели четыре свойства теории делимости.
. В этой лекции мы рассмотрели четыре свойства теории делимости. - Два положительных целых числа могут иметь больше чем один общий делитель. Но мы обычно интересуемся наибольшим общим делителем. Алгоритм Евклида дает эффективный и систематический алгоритм вычисления наибольшего общего делителя двух целых чисел.
- Расширенный алгоритм Эвклида может вычислить НОД (a, b) и вычислить значение s и t, которые удовлетворяют уравнению as + bt = НОД (a, b). Линейное диофантово уравнение двух переменных: ax + by = c. Оно имеет частное и общие решения.
- В модульной арифметике мы интересуемся только остатками; мы хотим знать значение r, когда мы делим a на n. Мы используем новый оператор, названный модулем (mod), такой, что a mod n = r. Здесь n называется модулем, а r называется вычетом.
- Результат операции по модулю n — всегда целое число от 0 и до n-1. Мы можем сказать, что операция по модулю n создает набор, который в модульной арифметике называется множеством наименьших вычетов по модулю n, или Zn.
- Отображение из Z в Zn не совпадают один в один. Определенные элементы Z могут быть отображены в элемент Zn. В модульной арифметике все целые числа в Z, отображаемые в Zn, называются сравнениями по модулю. Для обозначения этой операции применяется оператор сравнения (
 ).
). - Система вычетов [a] — множество целых чисел, сравнимых по модулю n. Это множество всех целых чисел x = a (mod n).
- Три бинарных операции (сложение, вычитание и умножение), определенные для множества Z, могут быть также определены для множества Zn. При необходимости результат может быть отражен в Zn при помощи операции mod.
- В этой лекции для модульных операторов были определены несколько свойств.
- В Zn два числа a и b — аддитивные инверсии по отношению друг к другу, если
 . Они — мультипликативные инверсии по отношению друг к другу, если
. Они — мультипликативные инверсии по отношению друг к другу, если 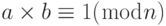 . Целое число a имеет мультипликативную инверсию в Zn тогда и только тогда, когда НОД (n, a) = 1 ( a и n — взаимно простые числа).
. Целое число a имеет мультипликативную инверсию в Zn тогда и только тогда, когда НОД (n, a) = 1 ( a и n — взаимно простые числа). - Расширенный алгоритм Евклида находит мультипликативные инверсии b в Zn, когда даны n и b и НОД (n, b) = 1. Мультипликативная инверсия b — это значение t при соответствующем отображении в Zn.
- Матрица — прямоугольный массив
 . элементы, где l является номером строки, а m — номер столбца. Мы обозначаем матрицу заглавной буквой и жирным шрифтом, например, A. Элемент aij расположен в i -той строке и j -том столбце.
. элементы, где l является номером строки, а m — номер столбца. Мы обозначаем матрицу заглавной буквой и жирным шрифтом, например, A. Элемент aij расположен в i -той строке и j -том столбце. - Две матрицы равны, если они имеют одинаковое число строк и столбцов и соответствующие элементы равны.
- Сложение и вычитание можно делать только для матриц равного размера. Мы можем умножить друг на друга две матрицы различных размеров, если число столбцов первой матрицы совпадает с числом строк второй матрицы. В матрицах вычетов все элементы берутся из Zn.
- Все операции на матрицах вычетов проводятся в модульной арифметике.
- Матрица вычета имеет инверсию, если детерминант матрицы имеет инверсию.
- Уравнение
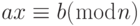 не может иметь решения или ограниченное число решений. Если НОД (a,n)|b, то имеется ограниченное число решений.
не может иметь решения или ограниченное число решений. Если НОД (a,n)|b, то имеется ограниченное число решений. - Система линейных уравнений с тем же самым модулем может быть решена, если матрица, сформированная из коэффициентов уравнений, имеет инверсию.
3.5. Набор для практики
Обзорные вопросы
- Покажите различие между Z и Zn. Какое из этих множеств может содержать отрицательные целые числа? Как мы можем отобразить целое число в Z в целое число в Zn?
- Перечислите четыре свойства теории делимости, обсужденной в этой лекции. Приведите пример целого числа с единственным делителем. Приведите пример целого числа только с двумя делителями. Приведите пример целого числа с более чем двумя делителями.
- Определите наибольший общий делитель двух целых чисел. Какой алгоритм может эффективно найти наибольший общий делитель?
- Что такое линейное диофантово уравнение двух переменных? Сколько решений может иметь такое уравнение? Как может быть найдено решение(я)?
- Что такое оператор по модулю и какие у него имеются приложения? Перечислите все свойства, которые мы упоминали в этой лекции для операций по модулю.
- Определите сравнение и сопоставьте его свойства со свойствами равенства.
- Определите систему вычетов и наименьший вычет.
- Какова разница между множеством Zn и множеством Zn*? В каком множестве каждый элемент имеет аддитивную инверсию? В каком множестве каждый элемент имеет мультипликативную инверсию? Какой алгоритм используется, чтобы найти мультипликативную инверсию целого числа в Zn?
- Дайте определение матрицы. Что такое матрица-строка? Что такое матрица-столбец? Что такое квадратная матрица? Какая матрица имеет детерминант? Какая матрица может иметь инверсию?
- Определите линейное сравнение. Какой алгоритм может использоваться, чтобы решить уравнение
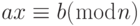 ? Как мы можем решить набор линейных уравнений?
? Как мы можем решить набор линейных уравнений?
Упражнения
- Какие из следующих отношений являются истинными, а какие — ложными?
5|26 3|123 27†127 15†21 23|96 8|5
- Используя алгоритм Эвклида, найдите наибольший общий делитель следующих пар целых чисел:
- 88 и 220
- 300 и 42
- 24 и 320
- 401 и 700
- Решите следующие примеры:
- Дано НОД (a, b) = 24, найдите НОД (a, b, 16)
- Дано НОД (a, b, c) = 12, найдите НОД (a, b, c, 16)
- Найдите НОД (200, 180, и 450)
- Найдите НОД (200, 180 450 610)
- Предположим, что n — неотрицательное целое число.
- Найдите НОД (2n + 1, n)
- Используя результат части а, найдите НОД (201, 100), НОД (81, 40) и НОД (501, 250)
- Предположим, что n — неотрицательное целое число.
- Найдите НОД (3 n + 1,2n +1).
- Используя результат части а, найдите НОД (301, 201) и НОД (121, 81)
- Используя расширенный алгоритм Евклида, найдите наибольший общий делитель следующих пар и значения s и t:
- 4 и 7
- 291 и 42
- 84 и 320
- 400 и 60
- Найдите результаты следующих операций:
- 22 mod 7
- 140 mod 10
- -78 mod 13
- 0 mod 15
- Выполните следующие операции, сначала используя следующее сокращение:
- (273 + 147) mod 10
- (4223 + 17323) mod 10
- (148 + 14432) mod 12
- (2467+461) mod 12
- Выполните следующие операции, сначала используя следующее сокращение:
- Используя свойства оператора mod, докажите следующее:
- Остаток от любого целого числа, когда оно делится на 10, — самая правая цифра
- Остаток от любого целого числа, когда оно делится на 100, — целое число, составленное из двух самых правых цифр
- Остаток от любого целого числа, когда оно делится на 1000, — целое число, составленное из трех самых правых цифр
- Из арифметики известно, что остаток от целого числа при делении на 5 — такой же, что и остаток от деления самой правой цифры на 5. Используйте свойства оператора mod, чтобы доказать это утверждение.
- Из арифметики известно, что остаток от целого числа при делении на 2 — такой же, что и остаток от деления самой правой цифры на 2. Используйте свойства оператора mod, чтобы доказать это утверждение.
- Из арифметики известно, что остаток от целого числа при делении на 4 — такой же, что и остаток от деления двух самых правых цифр на 4. Используйте свойства оператора mod, чтобы доказать это утверждение.
- Из арифметики известно, что остаток от целого числа при делении на 8 — такой же, что и остаток от деления самых правых трех цифр на 8. Используйте свойства оператора mod, чтобы доказать это утверждение.
- Из арифметики известно, что остаток от целого числа при делении на 9 — такой же, как и остаток от деления суммы его десятичных цифр на 9. Другими словами, остаток от деления 6371 на 9 — такой же, как при делении 17 на 9, потому что 6 + 3 + 7 + 1 = 17. Используйте свойства оператора mod, чтобы доказать это утверждение.
- Следующие упражнения показывают остатки от степени 10 при делении на 7. Мы можем доказать, что эти значения будут повторяться для более высоких степеней.
100 mod 7 = 1 101 mod 7 = 3 102 mod 7 = 2
103 mod 7 = 1 104 mod 7 = –3 105 mod 7 = –2
Используя вышеупомянутую информацию, найдите остаток от деления целого числа на 7. Проверьте ваш метод с числом 631453672.
- Следующие упражнения показывают остатки от деления степеней 10 на 11. Мы можем доказать, что эти значения будут повторяться для более высоких степеней
102 mod 11 = 1 101 mod 11 = –1 102 mod 11 = 1 103 mod 11 = –1
Используя вышеупомянутую информацию, найдите остаток от деления целого числа на 11. Проверьте ваш метод с числом 631453672.
- Следующие упражнения показывают остатки от деления степеней 10 на 13. Мы можем доказать, что эти значения будут повторяться для более высоких степеней.
102 mod 13 = 1 101 mod 13 = –3 102 mod 13 = –4
103 mod 3 = –1 104 mod 13 = 3 105 mod 13 = 4
Используя вышеупомянутую информацию, найдите остаток от целого числа при делении на 13. Проверьте ваш метод с числом 631453672.
- Назначим числовые значения для заглавных букв латинского алфавита
( A = 0, B = 1... Z = 25 ). Мы можем создать модульную арифметику, используя модуль 26.
- Что является (A + N) mod 26 в этой системе?
- Чему равно (A + 6) mod 26 в этой системе?
- Чему равно (Y – 5) mod 26 в этой системе?
- Чему равно (C – 10) mod 26 в этой системе?
- Перечислите все пары аддитивной инверсии по модулю 20.
- Перечислите все мультипликативные обратные пары по модулю 20.
- Найдите мультипликативную инверсию каждого из следующих целых чисел в Z180, используя расширенный алгоритм Евклида.
- 38
- 7
- 132
- 24
- Найдите частное и общие решения следующих линейных диофантовых уравнений:
- 25x + 10y = 15
- 19x + 13y = 20
- 14x + 21y = 77
- 40x +16y = 88
- Покажите, что нет ни одного решения следующих линейных диофантовых уравнений:
- 15x + 12y = 13
- 18x + 30y = 20
- 15x + 25y = 69
- 40x +30y = 98
- Почтовое отделение продает марки только за 15 центов и за 39 центов. Найдите число марок, которые должен купить клиент, чтобы оплатить пересылку пакета стоимостью 2,70$. Найдите несколько решений.
- Найдите все решения каждого из следующих линейных уравнений:
- Найдите все решения каждого из следующих линейных уравнений:
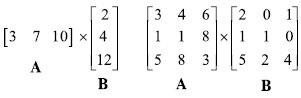
- Найдите
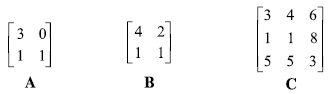
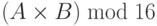 , используя матрицы на рис. 3.11.
, используя матрицы на рис. 3.11.
- На рисунке 3.12 найдите детерминант и мультипликативную инверсию для каждой матрицы вычетов в множестве Z10.
- Найдите все решения для следующих систем линейных уравнений:
-
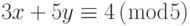 и
и 
-
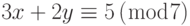 и
и 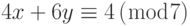
-
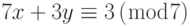 и
и 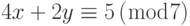
-
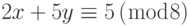 и
и 
-