Орграфы
Турниры
Турниром называется орграф, в котором любые две вершины соединены ровно одной дугой (см. рис. 9.5).
Основанием для выбора такого названия служит то, что подобные орграфы
можно использовать для записи результатов теннисных или любых других
турниров, в которых не разрешены ничьи. Например, на (рис. 9.5) представлены
результаты турнира, в котором команда  нанесла поражение
команде
нанесла поражение
команде  ,
но проиграла команде
,
но проиграла команде  , и т.д.
, и т.д.
Поскольку турнир может обладать источником или стоком, турниры не являются в общем случае гамильтоновыми орграфами. Однако следующая теорема (принадлежащая Реди и Камиону) показывает, что всякий турнир почти гамильтонов.
Теорема 9.3 (Реди, Камион).
- Всякий турнир полугамильтонов.
- Всякий сильно связный турнир гамильтонов.
Доказательство 1. Если турнир имеет меньше четырех вершин, то утверждение,
очевидно, верно. Проведем индукцию по числу вершин. Предположим, что любой
турнир с  вершинами полугамильтонов. Пусть
вершинами полугамильтонов. Пусть  — турнир с
— турнир с  вершинами, и пусть турнир
вершинами, и пусть турнир 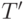 с
с  вершинами получен
из
вершинами получен
из  удалением
некоторой вершины
удалением
некоторой вершины  вместе со всеми инцидентными ей дугами.
Тогда, по предположению индукции,
вместе со всеми инцидентными ей дугами.
Тогда, по предположению индукции,  обладает полугамильтоновой простой
орцепью
обладает полугамильтоновой простой
орцепью  . Рассмотрим три
случая.
. Рассмотрим три
случая.
- Если
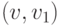 — дуга в
— дуга в  , то искомой
простой орцепью является
, то искомой
простой орцепью является 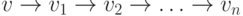 .
. - Если
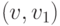 не является дугой в
не является дугой в  , это
означает, что дугой является
, это
означает, что дугой является 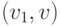 и если существует такое
и если существует такое  , что
, что 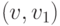 — дуга в
— дуга в  , то выбирая первое
, то выбирая первое  с таким свойством,
получим, что искомой простой орцепью является
с таким свойством,
получим, что искомой простой орцепью является 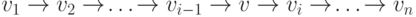 (см. рис. 9.6).
(см. рис. 9.6). - Если в
 не существует дуги вида
не существует дуги вида  , то
искомой простой орцепью является
, то
искомой простой орцепью является 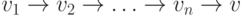 .
.
2. Докажем более сильный результат, состоящий в том, что сильно связный
турнир  с
с  вершинами содержит орциклы длин
вершинами содержит орциклы длин  .
.
Сначала покажем, что  содержит орцикл длины три. Для этого
выберем в
содержит орцикл длины три. Для этого
выберем в  произвольную вершину
произвольную вершину  и обозначим
через
и обозначим
через  множество всех
вершин
множество всех
вершин  , таких, что
, таких, что 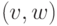 — дуга
в
— дуга
в  , а через
, а через  —
обозначим множество всех вершин
—
обозначим множество всех вершин  , таких, что
, таких, что 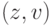 — дуга в
— дуга в  .
Так как
.
Так как  сильно связен, то оба множества
сильно связен, то оба множества  и
и  не пусты,
и поэтому в
не пусты,
и поэтому в  найдется дуга вида
найдется дуга вида 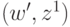 ,
где
,
где 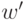 принадлежит
принадлежит  ,
,  принадлежит
принадлежит  .
Тогда требуемым циклом длины три является
.
Тогда требуемым циклом длины три является 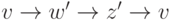 .
.
Осталось только показать, что если существует орцикл длины 
 ,
то существует и орцикл длины
,
то существует и орцикл длины  . Пусть
. Пусть 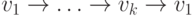 — орцикл длины
— орцикл длины  . Предположим сначала, что
в
. Предположим сначала, что
в  существует
вершина
существует
вершина  , не принадлежащая этому орциклу и обладающая тем
свойством, что в
, не принадлежащая этому орциклу и обладающая тем
свойством, что в  содержатся дуги вида
содержатся дуги вида  и вида
и вида  . Тогда должна существовать такая вершина
. Тогда должна существовать такая вершина 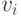 , что
и
, что
и  ,
и
,
и  являются дугами в
являются дугами в  . При этом требуемым
орциклом является (рис. 9.7)
. При этом требуемым
орциклом является (рис. 9.7)
 .
.
Если не существует вершин, обладающих указанным выше свойством, то
множество вершин, не содержащихся в орцикле, можно разбить на два
непересекающихся множества  и
и  ,
где
,
где  есть множество
таких вершин
есть множество
таких вершин  , что
, что 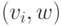 для
любого
для
любого  является дугой,
а
является дугой,
а  есть множество таких вершин
есть множество таких вершин  ,
что
,
что  для любого
для любого  является дугой. Так как
является дугой. Так как  сильно связен, то оба
множества
сильно связен, то оба
множества  и
и  непусты, и поэтому в
непусты, и поэтому в  найдется дуга
вида
найдется дуга
вида 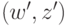 ,
где
,
где 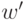 принадлежит
принадлежит  , а
, а  принадлежит
принадлежит  . Тогда требуемым орциклом будет (рис. 9.8)
. Тогда требуемым орциклом будет (рис. 9.8)
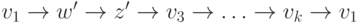 .
.





