|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Криптографическая система RSA
Некоторые тривиальные примеры
Рассмотрим некоторые тривиальные (ненадежные) примеры процедуры RSA. Критерии, которые делают систему RSА безопасной, будут обсуждены в более поздних разделах.
Пример 14.5
Боб выбирает 7 и 11 как p и q и вычисляет 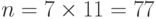 . Значение
. Значение  или 60. Теперь он выбирает два ключа, e и d, из Z60*. Если он выбирает e = 13, то d = 37. Обратите внимание, что
или 60. Теперь он выбирает два ключа, e и d, из Z60*. Если он выбирает e = 13, то d = 37. Обратите внимание, что 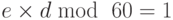 (они инверсны друг другу). Теперь предположим, что Алиса хочет передать исходный текст 5 Бобу. Она использует общедоступный ключ 13, чтобы зашифровать 5.
(они инверсны друг другу). Теперь предположим, что Алиса хочет передать исходный текст 5 Бобу. Она использует общедоступный ключ 13, чтобы зашифровать 5.
Исходный текст:5 C = 513 = 26 mod 77 Зашифрованный текст: 26
Боб получает зашифрованный текст 26 и использует секретный ключ 37, чтобы расшифровать зашифрованный текст.
Зашифрованный текст: 26 P = от 2637 до 5 mod 77 Исходный текст 5
Переданный Алисой текст получен Бобом как исходный текст 5.
Пример 14.6
Теперь предположим, что другой человек, Джон, хочет передать сообщение Бобу. Джон может использовать открытый ключ доступа, объявленный Бобом (вероятно, на его сайте), - 13 ; исходный текст Джона — 63. Джон делает следующие вычисления:
Исходный текст: 63 C = 6313 = 28 mod 77 Зашифрованный текст: 28
Боб получает зашифрованный текст 28 и использует свой секретный ключ 37, чтобы расшифровать зашифрованный текст.
Зашифрованный текст: 28 P = 2837 = 63 mod 77 Исходный текст: 63
Пример 14.7
Дженнифер создает пару ключей для себя. Она выбирает p = 397 и q = 401. Она вычисляет  . Затем она вычисляет
. Затем она вычисляет  . Затем она выбирает e = 343 и d = 12007. Покажите, как Тэд может передать сообщение "No" Дженнифер, если он знает e и n.
. Затем она выбирает e = 343 и d = 12007. Покажите, как Тэд может передать сообщение "No" Дженнифер, если он знает e и n.
Решение
Предположим, что Тэд хочет передать сообщение "No" Дженнифер. Он изменяет каждый символ на число (от 00 до 25 ), сопоставляет каждой букве число, содержащее две цифры. Затем он связывает два кодированных символа и получает четырехзначное число. Исходный текст — 1314. Затем Тэд использует e и n, чтобы зашифровать сообщение. Зашифрованный текст 1314343 = 33677 mod 159197. Дженнифер получает сообщение 33677 и использует d ключ дешифрования, чтобы расшифровать это сообщение: 3367712007 = 1314 mod 159197. Затем Дженнифер расшифровывает 1314 как сообщение "No". Рисунок 14.7 показывает этот процесс.
Атаки RSА
До настоящего момента не было обнаружено никаких разрушительных атак RSА. Несколько атак были предсказаны. Они основаны на слабом исходном тексте, слабом выборе параметра или несоответствующей реализации. Рисунок 14.8 показывает категории потенциальных атак.
Атака разложения на множители
Безопасность RSА базируется на следующей идее: модуль настолько большой, что разложение на множители в разумное время неосуществимо. Боб выбирает p и q и вычисляет 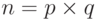 . Число n общедоступно, p и q являются секретными. Если Ева сможет разложить на множители n и получить p и q, то она может вычислить
. Число n общедоступно, p и q являются секретными. Если Ева сможет разложить на множители n и получить p и q, то она может вычислить  . Затем Ева тогда может вычислить
. Затем Ева тогда может вычислить  , потому что e общедоступен. Секретный ключ d — лазейка, которую Ева может использовать, чтобы расшифровать зашифрованное сообщение.
, потому что e общедоступен. Секретный ключ d — лазейка, которую Ева может использовать, чтобы расшифровать зашифрованное сообщение.
Как мы узнали в лекциях 12-13, есть много алгоритмов разложения на множители, но ни один из них не может найти сомножители большого целого числа с полиномиальной сложностью времени. Для того чтобы обеспечить безопасность, RSA требует, чтобы n был больше чем 300 десятичных цифр. Это означает, что модуль должен быть по крайней мере 1024 бита. Даже при использовании мощнейшего и самого быстрого компьютера, доступного на сегодня, разложение на множители целого числа такого размера требует неосуществимо большого времени. Это означает, что RSA безопасен, пока не будет найден эффективный алгоритм разложения на множители.
Атака с выборкой зашифрованного текста
Потенциальная атака RSА базируется на мультипликативном свойстве RSA. Предположим, Алиса создает зашифрованный текст C = Pe mod n и передает C Бобу. Также предположим, что Боб расшифрует произвольный зашифрованный текст для Евы – С1, отличный от C. Ева перехватывает C и использует следующие шаги, чтобы найти P:
а. Ева выбирает случайное целое число X в Zn*.
б. Ева вычисляет 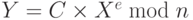 .
.
в. Ева передает Y Бобу для дешифрования и получает Z = Yd mod n ; это шаг атаки выборкой зашифрованного текста.
г. Ева может легко найти P, потому что
Z = Yd mod n = (C x Xe)d mod n = (Cd x Xed) mod n = (Cd x X) mod n = (P x X) mod n Z = (P x X) mod n -> P=Z x X-1 mod n
Ева использует расширенный евклидов алгоритм для того, чтобы найти мультипликативную инверсию X, и в конечном счете значение P.
Атаки на показатель степени шифрования
Чтобы уменьшить время шифрования, можно попытаться использовать короткий ключ шифрования — малое значение числа e, например, значение для e, такое как e = 3 (второе простое число). Однако есть некоторые потенциальные атаки на показатель при его малом значении степени шифрования, которые мы здесь кратко обсуждаем. Эти атаки вообще не кончаются вскрытием системы, но они все-таки должны быть предотвращены. Для того чтобы сорвать эти виды атак, рекомендуется использовать e = 216 + 1 = 65537 (или простое число, близкое к этому значению).
Атака теоремы Куперcмита (Coppersmith) может быть главной для атаки малого показателя степени на ключ шифрования. Основное положение этой теоремы: для полинома f(x) степени e по модулю n, чтобы найти корни, если один из корней является меньшим чем n1/e, можно использовать алгоритм сложности, log n. Эта теорема может быть применена к RSA-криптосистеме C = f(P) = Pe mod n. Если e = 3 и известны хотя бы две трети битов в исходном тексте P, алгоритм может найти все биты в исходном тексте.
Атака широковещательной передачи может быть начата, если один объект передает одно и то же сообщение группе получателей с тем же самым ключом шифрования. Например, предположим следующий сценарий: Алиса хочет передать одно и то же сообщение трем получателям с тем же самым общедоступным ключом e = 3 и модулями n1, n2 и n3.
C1 = P3 mod n1 C2 = P3 mod n2 C3 = P3 mod n3
Применяя китайскую теорему об остатках к этим трем уравнениям, Ева может найти уравнение формы C’ = P3 mod n1n2n3. Это означает, что P3 < n1n2n3 и что C’ = P3 решается с помощью обычной арифметики (не модульной). Ева может найти значение C’ = P1/3.
Атака связанных между собой сообщений была обнаружена Франклином Рейтером (Franklin Reiter). Она может быть кратко описана следующим образом. Алиса зашифровала два исходных текста, P1 и P2, с помощью e = 3 и передает C1 и C2 Бобу. Если P1 связан с P2 линейной функцией, то Ева может восстановить P1 и P2 в выполнимое время вычисления.
Атака короткого списка, обнаруженная Куперсмитом, может быть кратко описана следующим образом. Алиса имеет сообщение М для передачи Бобу. Она записывает сообщение и зашифровывает его как сообщение r1, а результат записывает как C1 и передает C1 (Бобу). Ева перехватывает C1 и удаляет его. Боб сообщает Алисе, что он не получил сообщение, так что Алиса заполняет сообщение, снова зашифровывает как сообщение r2 и передает это Бобу. Ева также перехватывает и это сообщение. Ева теперь имеет C1 и C2, и она знает, что оба зашифрованных текста принадлежат одному и тому же исходному тексту. Куперсмит доказал, что если r1 и r2 короткие, то Ева способна восстановить первоначальное сообщение М.
Атаки показателя степени дешифрации
Две формы атак могут быть проведены на показатель степени дешифрации: атака раскрытой степени дешифрации и атака малого показателя степени дешифровации. Они обсуждаются ниже.
Атака раскрытого показателя степени дешифрации. Очевидно, что если Ева может найти показатель степени дешифрации, d, она сможет расшифровать текущее зашифрованное сообщение. Однако на этом атака не останавливается. Если Ева знает значение d, она может использовать вероятностный алгоритм (не обсуждаемый здесь) к числу n и найти значения p и q. Следовательно, если Боб изменит только угрожающий безопасности показатель степени дешифрования, но сохранит тот же самый модуль n, Ева сможет расшифровать будущие сообщения, потому что она сможет разложить на множители n. Поэтому если Боб узнает, что показатель степени скомпрометирован, он должен выбрать новое значение для p и q, вычислить n и создать полностью новые секретный и открытый ключи доступа.
Атака малого значения показателя степени дешифрации. Боб может подумать, что использование малого значения степени секретного ключа d приводит к более быстрой работе алгоритма дешифрации. Винер показал, что в случае d < 1/3n1/4 возможен специальный тип атаки, основанной на цепной дроби, — тема, которая рассматривается в теории чисел. Этот тип атаки может подвергнуть риску безопасность RSА. Для того чтобы это произошло, должно выполняться условие, что q < p < 2q; если эти два условия существуют, Ева может разложить n на сомножители в полиномиальное время.
Атаки исходного текста
Исходный текст и зашифрованный текст в RSA — это перестановки друг друга, потому что это целые числа в том же самом интервале (от 0 до n – 1 ). Другими словами, Ева уже знает кое-что об исходном тексте. Эти характеристики могут позволить некоторые атаки исходного текста. Три атаки были уже упомянуты в литературе: атака короткого сообщения, атака циклического повторения и явная атака.
Атака короткого сообщения. В атаке короткого сообщения, если Ева знает множество возможных исходных текстов, то ей известна еще одна информация и дополнительный факт, что зашифрованный текст — перестановка исходного текста. Ева может зашифровать все возможные сообщения, пока результат не будет совпадать с перехваченным зашифрованным текстом. Например, если известно, что Алиса посылает число с четырьмя цифрами Бобу, Ева может легко испытать числа исходного текста 0000 к 9999, чтобы найти исходный текст. По этой причине короткие сообщения должны быть дополнены случайными битами в начале и конце, чтобы сорвать этот тип атаки. Настоятельно рекомендуется заполнять исходный текст случайными битами прежде начала шифрования. Здесь используется метод, называемый OAEP, который будет позже обсужден в этой лекции.
Атака циклического повторения построена на факте, что если переставлять зашифрованный текст (перестановка исходного текста), то непрерывное шифрование зашифрованного текста в конечном счете кончится исходным текстом. Другими словами, если Ева непрерывно шифрует перехваченный зашифрованный текст C, она в итоге получит исходный текст. Однако сама Ева не знает, каков исходный текст, так что ей неизвестно, когда пора остановиться. Она должна пройти один шаг далее. Когда она получает зашифрованный текст C снова, она возвращается на один шаг, чтобы найти исходный текст.
Перехваченный зашифрованный текст C C1 = Ce mod n C2 = C1e mod n ……………… Ck = Ck-1e mod n ->, если Ck = C, останов: исходный текст - P = Ck-1
Может ли это быть серьезной атакой на криптосистему RSA? Показано, что сложность алгоритма эквивалентна сложности разложения на множители n. Другими словами, нет никакого эффективного алгоритма, который может завершить эту атаку в полиномиальное время, если n является большим.
Явная атака сообщения. Другая атака, которая базируется на отношениях перестановки между исходным текстом и зашифрованным текстом, — явная атака сообщения. Явное сообщение — сообщение, которое зашифровано само в себя (не может быть скрыто). Было доказано, что есть всегда некоторые сообщения, которые шифруются сами в себя. Поскольку ключ шифрования обычно нечетен, имеются некоторые исходные тексты, которые зашифрованы сами в себя, такие как P = 0 и P = 1. Но если ключ шифровки выбран тщательно, число их незначительно. Программа шифровки может всегда проверить, является ли вычисленный зашифрованный текст таким же, как исходный текст, и отклонить  исходный текст перед передачей зашифрованного текста.
исходный текст перед передачей зашифрованного текста.
Атаки модуля
Главной атакой RSA является атака разложения на множители. Ее можно рассматривать как атаку малого модуля. Однако поскольку мы уже обсудили эту атаку, мы концентрируемся на другой атаке модуля: общей атаке модуля.
Общая атака модуля. Она может быть начата, если сообщество  использует общий модуль, n. Например, люди в сообществе могли бы позволить третьей стороне, которой они доверяют, выбирать p и q, вычислять n и
использует общий модуль, n. Например, люди в сообществе могли бы позволить третьей стороне, которой они доверяют, выбирать p и q, вычислять n и  и создать пару образцов ( ei, di ) для каждого объекта. Теперь предположим, что Алиса должна передать сообщение Бобу. Зашифрованный текст Бобу — это
и создать пару образцов ( ei, di ) для каждого объекта. Теперь предположим, что Алиса должна передать сообщение Бобу. Зашифрованный текст Бобу — это  Боб использует свой секретный ключ, dB, чтобы расшифровывать сообщение:
Боб использует свой секретный ключ, dB, чтобы расшифровывать сообщение:  . Проблема в том, что Ева может также расшифровать сообщение, если она — член сообщества и ей была назначена пара образцов ( eE и dE ), как мы узнали в разделе "атака малого значения ключа дешифрации". Используя свои собственные ключи ( eE и dE ), Ева может начать вероятностную атаку на сомножители n и найти dB Боба. Чтобы сорвать этот тип атаки, модуль не должен быть в совместном пользовании. Каждый объект должен вычислить свой собственный модуль.
. Проблема в том, что Ева может также расшифровать сообщение, если она — член сообщества и ей была назначена пара образцов ( eE и dE ), как мы узнали в разделе "атака малого значения ключа дешифрации". Используя свои собственные ключи ( eE и dE ), Ева может начать вероятностную атаку на сомножители n и найти dB Боба. Чтобы сорвать этот тип атаки, модуль не должен быть в совместном пользовании. Каждый объект должен вычислить свой собственный модуль.
Атаки реализации
Предыдущие атаки базировались на основной структуре RSА. Как показал Дэн Бонех (Dan Boneh), есть несколько атак реализации RSА. Мы приведем две из них: атака анализом времени и атака мощности.
Атака анализом времени (Timing attack). Пауль Кочер (Paul Kocher) демонстрировал атаку только зашифрованного текста, называемую атака анализом времени. Атака основана на быстром алгоритме с показательным временем, который рассмотрен в лекциях 12-13. Алгоритм использует только возведение во вторую степень, если соответствующий бит в секретном показателе степени d есть 0 ; он используется и при возведении во вторую степень и умножении, если соответствующий бит — 1. Другими словами, синхронизация требует сделать каждую итерацию более длинной, если соответствующий бит — 1. Эта разность синхронизации позволяет Еве находить значение битов в d, один за другим.
Предположим, что Ева перехватила большое количество зашифрованных текстов от C1 до Cm. Также предположим, что Ева наблюдала, какое количество времени требуется для Боба, чтобы расшифровать каждый зашифрованный текст, от T1 до T2. Ева знает, сколько времени требуется для основных аппаратных средств, чтобы выполнить операцию умножения от t1 до tm., где t1 — время, требуемое для выполнения умножения.
Результат операции умножения = Результат  .
Ева может использовать алгоритм 14.5, который является упрощенной версией алгоритма, используемого практически для вычисления всех бит в d ( d0 до d k-1 ).
.
Ева может использовать алгоритм 14.5, который является упрощенной версией алгоритма, используемого практически для вычисления всех бит в d ( d0 до d k-1 ).
Алгоритм устанавливает начальное значение d0 = 1 (потому что d должен быть нечетным) и вычисляет новые значения для T’is (время дешифрования относится к d1 до dk-1 ). Алгоритм затем предполагает, что следующий бит — это 1, и находит несколько значений D1 до D2, основываясь на этом предположении.
RSA_Timing_Attack([T1…Tm])
{
d0 <- 1 // Потому что d — нечетное
Вычислить [t1…tm]
[T1…Tm] <- [T1…Tm] - [t1…tm]
for (j from 1 to k-1)
{ //Обновление Ti для следующего бита
Пересчитать [t1…tm]
//Пересчет ti в предположении, что следующий бит — это 1
[D1…Dm] <- [T1…Tm] -[t1…tm]
var <- variance ([D1…Dm]) – variance ([T1…Tm])
if (var > 0) dj <- 1 else dj <- 0
[T1…Tm] <- [T1…Tm] - dj x [t1…tm] //Обновление Ti для следующего бита
}
}
14.5.
Атака синхронизации
Если принятое предположение верно, то каждый Di является вероятно меньшим, чем соответствующее время передачи Ti. Однако алгоритм использует дисперсию (или другие критерии корреляции), чтобы рассмотреть все варианты Di и Ti. Если разность дисперсии положительная, алгоритм принимает предположение, что следующий бит равен 1 в противном случае предполагает, что следующий бит — 0. Алгоритм тогда вычисляет новые Ti, используя для этого оставшиеся биты.
Есть два метода сорвать атаку анализом времени:
1. добавить случайные задержки к возведению в степень, чтобы каждое возведение в степень занимало одно и то же время;
2. Ривест рекомендовал "ослепление". По этой идее зашифрованный текст умножается на случайное число перед дешифрованием. Процедура содержит следующие шаги:
a. Выбрать секретное случайное число r между 1 и (n – 1).
b. Вычислить 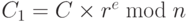 .
.
c. Вычислить P1 = C1d mod n.
d. Вычислить 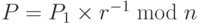 .
.
Атака анализом мощности подобна атаке анализом времени. Было показано, что если Ева может точно измерить мощность, использованную в течение дешифрования, она может начать атаку анализа мощности на основании принципов, рассмотренных для атаки анализом времени. Итеративное умножение и возведение в квадрат потребляют больше мощности, чем только итеративное возведение в квадрат. Та же самая группа методов, которая предотвращает атаки анализом времени, может сорвать атаки анализа мощности.



