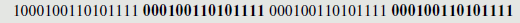|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Введение в основы современных шифров с симметричным ключом
7.2. Современные шифры потока
В лекциях 5-6 мы кратко обсуждали разницу между традиционными шифрами потока и традиционными блочными шифрами. Подобные отличия существуют также между современными шифрами потока и современными блочными шифрами. В современном шифре потока шифрование и дешифрование проводятся r бит одновременно. Мы имеем поток бит исходного текста P = pn… p2p1, поток бит зашифрованного текста C = cn ... c2 c1, и ключевой поток бит K = k n ... k2k1, в которых pi ci, и ki — это r -битные слова. Шифрование — ci = E (ki,pi), и дешифрование — pi = D (ki, ci), как показывает рис. 7.21.
Шифры потока быстрее, чем блочные шифры. Аппаратная реализация шифра потока также более проста. Когда мы должны зашифровать двоичные потоки и передать их на постоянной скорости, лучший выбор — использовать шифр потока. Шифры потока обладают большей защитой против искажения битов в течение передачи.
Рассматривая рис. 7.21, можно предположить, что главная проблема в современных шифрах потока — как генерировать ключевой поток K = kn….. k2k1. Современный шифр потока можно разделить на две обширные категории: синхронный и несинхронный.
Синхронные шифры потока
В синхронном шифре потока ключевой поток независим от потока зашифрованного текста или исходного текста. Ключевой генерируемый поток не используется без отношений между ключевыми битами и исходным текстом или битами зашифрованного текста.
Одноразовый блокнот
Наиболее простой и самый безопасный тип синхронного шифра потока назван шифром одноразового блокнота, или, по имени изобретателя, "шифром Вернама". Шифр одноразового блокнота использует ключевой поток, который беспорядочно выбран для каждой шифровки. Алгоритмы шифрования и дешифрования применяют единственную операцию — ИСКЛЮЧАЮЩЕЕ ИЛИ. Шифры, которые базируются на свойствах операции ИСКЛЮЧАЮЩЕЕ ИЛИ, обсуждались ранее. В них алгоритмы шифрования и дешифрования инверсны друг другу. Важно, что в этом шифре операция ИСКЛЮЧАЮЩЕЕ ИЛИ используется только для одного бита одновременно. Другими словами, операция производится над словом не более чем из одного бита и полем GF (2). Заметим, что также нужно иметь безопасный канал для того, чтобы Алиса могла передать ключевую последовательность потока Бобу (рис. 7.22).
Одноразовый блокнот — идеальный шифр. Он совершенен. Нет метода, который дал бы противнику возможность распознать ключ или статистику зашифрованного текста и исходного текста. Нет никаких соотношений между исходным и зашифрованным текстами. Другими словами, зашифрованный текст – настоящий случайный поток битов, даже если получить некоторые образцы исходного текста. Ева не может нарушить шифр, если она не попробует все возможные случайные ключевые потоки, которые были бы 2n, если размер исходного текста — n -битовый. Однако при этом есть проблема. Передатчик и приемник для того, чтобы совместно использовать одноразовый блокнот ключей, должны установить соединение каждый раз, когда они хотят обменяться информацией. Они должны, так или иначе, договориться о случайном ключе. Так что этот совершенный и идеальный шифр очень трудно реализовать.
Пример 7.17
Какой вид имеет зашифрованный текст при использовании шифра одноразового блокнота в каждом из следующих случаев?
а. Исходный текст состоит из n нулей.
б. Исходный текст состоит из n единиц.
в. Исходный текст состоит из чередующихся нулей и единиц.
г. Исходный текст — случайная строчка бит.
Решение
a. Поскольку  , то поток зашифрованного текста совпадет с ключевым потоком. Если ключ случайный, зашифрованный текст также случайный. Отрывки исходного текста в зашифрованном тексте не сохраняются.
, то поток зашифрованного текста совпадет с ключевым потоком. Если ключ случайный, зашифрованный текст также случайный. Отрывки исходного текста в зашифрованном тексте не сохраняются.
b. Поскольку 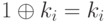 , где
, где  является дополнением, поток зашифрованного текста — дополнение ключевого потока. Если ключевой поток случайный, то зашифрованный текст также случайный, отрывки исходного текста не сохраняются в зашифрованном тексте.
является дополнением, поток зашифрованного текста — дополнение ключевого потока. Если ключевой поток случайный, то зашифрованный текст также случайный, отрывки исходного текста не сохраняются в зашифрованном тексте.
c. В этом случае каждый бит в потоке зашифрованного текста является или тем же самым, что и в ключевом потоке, или его дополнением. Поэтому результат — также случайный, если ключевой поток случайный.
d. В данном случае зашифрованный текст явно случайный, потому что проведение операции ИСКЛЮЧАЮЩЕЕ ИЛИ двух случайных битов в результате дает случайный поток бит.
Регистр сдвига с обратной связью
Одно усовершенствование к одноразовому блокноту — Регистр сдвига с обратной связью (FSR — Feedback Shift Register). FSR может быть реализован или в программном обеспечении, или в аппаратных средствах, но для простоты мы рассмотрим аппаратную реализацию. Регистр сдвига с обратной связью состоит из регистра сдвига и функции обратной связи, как показано на рис. 7.23.
Регистр сдвига – последовательность из m ячеек от b0 до bm-1, где каждая ячейка предназначена для сохранения единственного бита. Ячейки рассматриваются как n -битовое слово, называемое в начале "начальное значение" или источник. Всякий раз, когда необходимо получить бит на выходе (например, по сигналу в определенное время), каждый бит сдвигается на одну ячейку вправо. Это означает, что значение каждой ячейки присваивается правой соседней ячейке и принимает значение левой ячейки. Самая правая ячейка b0 считается выходом и дает выходное значение ( ki ). Крайняя левая ячейка, bm-1, получает свое значение согласно значению информации функции обратной связи. Обозначаем выход функции с информацией обратной связи bm. Функция информации обратной связи определяет, какие значения имеют ячейки, чтобы вычислить bm. Регистр сдвига информации обратной связи может быть линейный или нелинейный.
Линейный регистр сдвига с обратной связью (LFSR). Примем, что bm — это линейная функция b0, b1,…..., bm-1, для которой

Линейный регистр сдвига с обратной связью работает с двоичными цифрами, поэтому умножение и сложение находятся в поле GF(2), так что значение Ci является или 1, или 0, но C0 должно быть 1, чтобы получить информацию обратной связи на выходе. Операция сложения – это операция ИСКЛЮЧАЮЩЕЕ ИЛИ. Другими словами,

Пример 7.18
Построим линейный регистр сдвига с обратной связью с 5 -ю ячейками, в которых  .
.
Решение
Если Сi = 0, bi не играет роли в вычислении bm, то это означает, что bi не связан с функцией информации обратной связи. Если c i = 1, bi включается в вычисление bm. В этом примере c1 и c3 — нули, это означает, что, мы имеем только три подключения. Рисунок 7.24 показывает схему линейного регистра сдвига с обратной связью.
Пример 7.19
Построим линейный регистр сдвига с обратной связью с 4 -мя ячейками, в которых 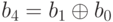 . Покажите значение регистра после 20 операций (сдвигов), если исходное значение — (0001) 2.
. Покажите значение регистра после 20 операций (сдвигов), если исходное значение — (0001) 2.
Решение
Рисунок 7.25 показывает схему и использование линейного регистра сдвига с обратной связью для шифрования.
Таблица 7.6. показывает значение потока ключей. Для каждого перехода первое значение b4 вычисляется, а затем каждый бит сдвигается на одну ячейку вправо.
| Текущее значение | b4 | b3 | b2 | b1 | b0 | ki |
|---|---|---|---|---|---|---|
| Начальное значение | 1 | 0 | 0 | 0 | 1 | |
| 1 | 0 | 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 | 0 | 0 |
| 3 | 1 | 0 | 0 | 1 | 0 | 0 |
| 4 | 1 | 1 | 0 | 0 | 1 | 0 |
| 5 | 0 | 1 | 1 | 0 | 0 | 1 |
| 6 | 1 | 0 | 1 | 1 | 0 | 0 |
| 7 | 0 | 1 | 0 | 1 | 1 | 0 |
| 8 | 1 | 0 | 1 | 0 | 1 | 1 |
| 9 | 1 | 1 | 0 | 1 | 0 | 1 |
| 10 | 1 | 1 | 1 | 0 | 1 | 0 |
| 11 | 1 | 1 | 1 | 1 | 0 | 1 |
| 12 | 0 | 1 | 1 | 1 | 1 | 0 |
| 13 | 0 | 0 | 1 | 1 | 1 | 1 |
| 14 | 0 | 0 | 0 | 1 | 1 | 1 |
| 15 | 1 | 0 | 0 | 0 | 1 | 1 |
| 16 | 0 | 1 | 0 | 0 | 0 | 1 |
| 17 | 0 | 0 | 1 | 0 | 0 | 0 |
| 18 | 1 | 0 | 0 | 1 | 0 | 0 |
| 19 | 1 | 1 | 0 | 0 | 1 | 0 |
| 20 | 1 | 1 | 1 | 0 | 0 | 1 |
Заметим, что поток ключей — 1000100110101111 1001…… . Он выглядит, на первый взгляд, как случайная последовательность, но если просмотреть большое число транзакций (сдвигов), мы можем увидеть, что последовательности периодичны. Это повторение по 15 бит показано ниже.
Ключ потока генерирует с помощью линейного регистра сдвига с обратной связью псевдослучайную последовательность, в которой повторяются последовательности длиною N. Поток периодичен. Он зависит от схемы генератора и начальной информации и может быть не свыше 2m – 1. Каждая схема порождает m -битовые последовательности от содержащих все нули до содержащих все единицы. Однако если начальная последовательность состоит только из нулей, результат бесполезен — исходный текст был бы потоком из одних нулей. Поэтому такая начальная последовательность исключена.
В предыдущем примере максимальный период — ( 24 – 1 = 15 ). Чтобы достичь этой максимальной периодичности (наилучшей рандомизации), мы должны в первую очередь представить функцию обратной связи как характеристический полином с коэффициентами в поле GF(2).
bm = cm-1bm-1 + … + c1b1 + c0b0 -> xm = cm-1xm-1 + … + c1x1 + c0x0
Поскольку сложение и вычитание в этом поле одни и те же, все элементы могут быть перенесены в одну сторону, что дает полином степени m. (называемый характеристическим полиномом).
xm + cm-1xm-1 + … + c1x1 + c0x0 = 0
Линейный регистр сдвига с обратной связью имеет максимальный период 2m–1, если он имеет четное число ячеек, и характеристический полином — примитивный полином. Примитивный полином — неприводимый полином, который является делителем xe –1, где e — наименьшее целое число в форме e = 2k–1 и k >= 2. Примитивный полином получить нелегко. Полином выбирается случайно, а затем проверяется на примитивность. Однако существуют таблицы проверенных примитивных полиномов (см. приложение G).
Пример 7.20
Характеристический полином для линейного регистра сдвига с обратной связью в примере 7.19 — ( x4 + x + 1 ) — является примитивным полиномом. Таблица 5.1 ( "Алгебраические структуры" ) показывает, что это — неприводимый полином. Этот полином также делит (x7 + 1) = (x4 + x + 1) (x3 + 1), что означает e = 23 –1 = 7.
Атаки шифров, полученных с помощью линейных регистров сдвига с обратной связью.Линейный регистр сдвига с обратной связью имеет очень простую структуру, но эта простота делает шифр уязвимым к атакам. Два общих типа атаки приведены ниже.
- Если структура линейного регистра сдвига с обратной связью известна, то после перехвата и анализа одного n -битового куска зашифрованного текста Ева может предсказать все будущие зашифрованные тексты.
- Если структура линейного регистра сдвига с обратной связью неизвестна, Ева может использовать атаку знания исходного текста длиной 2n бит, чтобы вскрыть шифр.
Нелинейный регистр сдвига с обратной связью. Линейный регистр сдвига с обратной связью уязвим главным образом из-за его линейности. Более устойчивый шифр потока может быть получен при использовании нелинейного регистра сдвига с обратной связью(NLFSR). Он имеет ту же самую структуру, что и линейный регистр сдвига с обратной связью, за исключением того, что bm — нелинейная функция b0,b1, ….,bm. Например, в 4 -битном нелинейном регистре сдвига с обратной связью структура определяется соотношением, показанным ниже, где операция AND означает поразрядную операцию И, а OR означает поразрядную операцию ИЛИ. Черточка над переменной означает инверсию.
Однако нелинейный регистр сдвига с обратной связью не имеет общего характера, поскольку нет математического обоснования, как получить такой регистр с максимальным периодом.
Можно применить линейный регистр сдвига с обратной связью с максимальным периодом и затем скомбинировать его обратную связь с помощью нелинейной функции.
Несинхронные шифры потока
В несинхронном шифре потока каждый ключ в ключевом потоке зависит от предыдущего исходного текста или зашифрованного текста.
Два метода, которые используются, чтобы создать различные режимы работы для блочных шифров ( режим обратной связи по выходу и режим счета сцеплений блоков шифра ), фактически создают шифры потока (см. "Шифрование, использующее современные шифры с симметричным ключом" ).