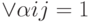Способы описания работы дискретных устройств
3.1 Общие сведения об управляющем автомате
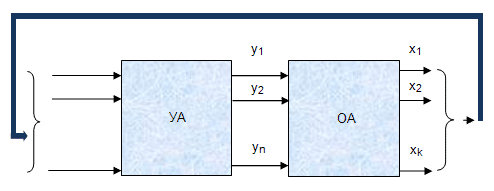
Цифровую систему можно представить в виде устройства переработки информации, состоящую из двух частей: операционной и управляющей (рис.3.1).
Операционная часть в этом случае представляет собой набор функциональных узлов типа счётчик, регистр, сумматор, дешифратор и т.п., с соответствующими связями. На базе этих функциональных узлов выполняются все элементарные операции из множества, определяемого видом зависимости 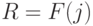 (рис.3.1)
(рис.3.1)
В большинстве случаев это операции передачи, сдвига, запоминания чисел, анализа сопровождающих указанные операции признаков. На практике набор операций варьируется в зависимости от конкретных технических требований (время решения задачи, тип системы элементов), однако во всех случаях он должен быть достаточным для решения задачи.
Процесс решения заключается в упорядоченном (программном) выполнении перечисленных выше элементарных операций и для своей технической реализации требует использования специального датчика программной распределенной во времени и в пространстве последовательности импульсов. Эти импульсы, воздействуя на соответствующие узлы операционной части, обеспечат упорядоченную последовательность выполнения элементарных операций (рис.3.2). Операционную часть можно назвать операционным автоматом (ОА).
Таким образом, выделенная ранее управляющая часть устройства преобразования информации может рассматриваться как некоторый блок, обеспечивающий программное управление процессом преобразования информации, то есть как управляющий автомат (УА). Сам же принцип программного управления сводится к упорядоченной (программной) выработке сигналов-команд, выполнение которых приводит к достижению заданной цели.
Основным элементом программного управления на рассматриваемом уровне является микрокоманда.
 -множество микрокоманд
-множество микрокоманд  микропрограммных автоматов как составной части устройств управления.
микропрограммных автоматов как составной части устройств управления.
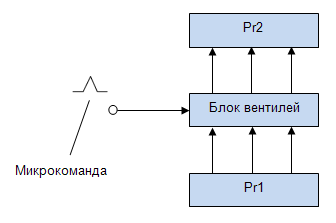
Микрокомандой в дальнейшем будем называть управляющий сигнал (потенциал, импульс), осуществляющий выполнение одного элементарного шага в процессе решения задачи (рис.3.3).
Микрооперация - наименование микрокоманды.
Микрокоманде, представленной на рис.3.3, соответствует микрооперация: "Передать число из Рг I в Рг2".
В каждом процессе управления можно выделить некоторое множество различных микроопераций, которое называется набором микроопераций.
 -микрокоманда, состоящая из микроопераций (МО)
-микрокоманда, состоящая из микроопераций (МО)
Микропрограмма представляет собой упорядоченную последовательность микроопераций заданного набора. Это определение является частным, т.к. охватывает только те случаи управления, когда последовательность управляющих сигналов не меняется в зависимости от некоторых признаков, сопровождающих процесс обработки информации. В общем же случае последовательность микроопераций может меняться в зависимости от признаков, сопровождающих процесс обработки информации. Поэтому в состав микропрограммы кроме микроопераций, вводят также условия, в зависимости от выполнения или невыполнения которых изменяется последовательность микроопераций. По признаку отсутствия или наличия условий, в зависимости от которых меняется последовательность микроопераций, все микропрограммы делятся на две группы: не разветвляющиеся и разветвляющиеся. Разветвляющиеся микропрограммы делятся, в свою очередь, на две группы: микропрограммы без циклов и микропрограммы с циклами. В общем случае микропрограммы могут содержать в качестве своих частей все три вида: не разветвляющиеся части, разветвляющиеся и циклические.
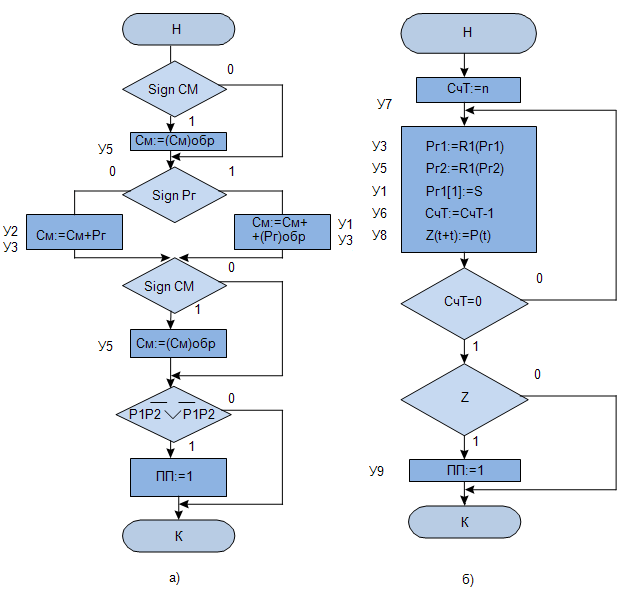
Например, на рис.3.4) показана МП операции сложения. Если ввести формальное переобозначение микрокоманд (  или
или 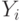 ), то для МП на рис.3.4,б получим ГСА
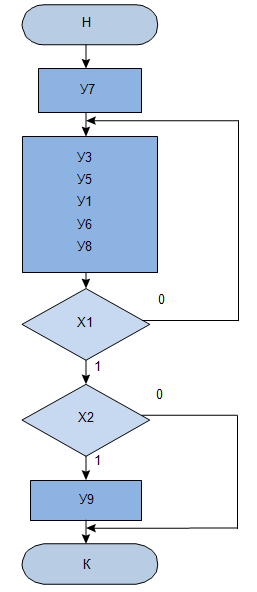
ГСА МП показанную на рис.3.5.
), то для МП на рис.3.4,б получим ГСА
ГСА МП показанную на рис.3.5.
Последовательность выполнения МК определяется функциями перехода
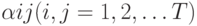 от множества логических переменных
от множества логических переменных 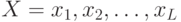 . Функции перехода обладают 2 свойствами: полноты и ортогональности.
. Функции перехода обладают 2 свойствами: полноты и ортогональности.
Свойство ортогональности говорит об однозначности перехода, а свойство полноты о том, что этот переход обязательно существует.
Способы формальной записи МП, удовлетворяющие перечисленным выше свойствам, это: