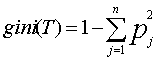Методы классификации и прогнозирования. Деревья решений

Преимущества деревьев решений

Интуитивность деревьев решений. Классификационная модель, представленная в виде дерева решений, является интуитивной и упрощает понимание решаемой задачи. Результат работы алгоритмов конструирования деревьев решений, в отличие, например, от нейронных сетей, представляющих собой "черные ящики", легко интерпретируется пользователем. Это свойство деревьев решений не только важно при отнесении к определенному классу нового объекта, но и полезно при интерпретации модели классификации в целом. Дерево решений позволяет понять и объяснить, почему конкретный объект относится к тому или иному классу.

Деревья решений дают возможность извлекать правила из базы данных на естественном языке. Пример правила: Если Возраст > 35 и Доход > 200, то выдать кредит.

Деревья решений позволяют создавать классификационные модели в тех областях, где аналитику достаточно сложно формализовать знания.

Алгоритм конструирования дерева решений не требует от пользователя выбора входных атрибутов (независимых переменных). На вход алгоритма можно подавать все существующие атрибуты, алгоритм сам выберет наиболее значимые среди них, и только они будут использованы для построения дерева. В сравнении, например, с нейронными сетями, это значительно облегчает пользователю работу, поскольку в нейронных сетях выбор количества входных атрибутов существенно влияет на время обучения.

Точность моделей, созданных при помощи деревьев решений, сопоставима с другими методами построения классификационных моделей (статистические методы, нейронные сети).

Разработан ряд масштабируемых алгоритмов, которые могут быть использованы для построения деревьев решения на сверхбольших базах данных; масштабируемость здесь означает, что с ростом числа примеров или записей базы данных время, затрачиваемое на обучение, т.е. построение деревьев решений, растет линейно. Примеры таких алгоритмов: SLIQ, SPRINT.

Быстрый процесс обучения. На построение классификационных моделей при помощи алгоритмов конструирования деревьев решений требуется значительно меньше времени, чем, например, на обучение нейронных сетей.

Большинство алгоритмов конструирования деревьев решений имеют возможность специальной обработки пропущенных значений.

Многие классические статистические методы, при помощи которых решаются задачи классификации, могут работать только с числовыми данными, в то время как деревья решений работают и с числовыми, и с категориальными типами данных.

Многие статистические методы являются параметрическими, и пользователь должен заранее владеть определенной информацией, например, знать вид модели, иметь гипотезу о виде зависимости между переменными, предполагать, какой вид распределения имеют данные. Деревья решений, в отличие от таких методов, строят непараметрические модели. Таким образом, деревья решений способны решать такие задачи Data Mining, в которых отсутствует априорная информация о виде зависимости между исследуемыми данными.

Процесс конструирования дерева решений

Напомним, что рассматриваемая нами задача классификации относится к стратегии обучения с учителем, иногда называемого индуктивным обучением. В этих случаях все объекты тренировочного набора данных заранее отнесены к одному из предопределенных классов.

Алгоритмы конструирования деревьев решений состоят из этапов "построение" или " создание " дерева (tree building) и " сокращение " дерева (tree pruning). В ходе создания дерева решаются вопросы выбора критерия расщепления и остановки обучения (если это предусмотрено алгоритмом). В ходе этапа сокращения дерева решается вопрос отсечения некоторых его ветвей.

Рассмотрим эти вопросы подробней.

Критерий расщепления

Процесс создания дерева происходит сверху вниз, т.е. является нисходящим. В ходе процесса алгоритм должен найти такой критерий расщепления, иногда также называемый критерием разбиения, чтобы разбить множество на подмножества, которые бы ассоциировались с данным узлом проверки. Каждый узел проверки должен быть помечен определенным атрибутом. Существует правило выбора атрибута: он должен разбивать исходное множество данных таким образом, чтобы объекты подмножеств, получаемых в результате этого разбиения, являлись представителями одного класса или же были максимально приближены к такому разбиению. Последняя фраза означает, что количество объектов из других классов, так называемых "примесей", в каждом классе должно стремиться к минимуму.

Существуют различные критерии расщепления. Наиболее известные - мера энтропии и индекс Gini.

В некоторых методах для выбора атрибута расщепления используется так называемая мера информативности подпространств атрибутов, которая основывается на энтропийном подходе и известна под названием "мера информационного выигрыша" (information gain measure) или мера энтропии.

Другой критерий расщепления, предложенный Брейманом (Breiman) и др., реализован в алгоритме CART и называется индексом Gini. При помощи этого индекса атрибут выбирается на основании расстояний между распределениями классов.

Если дано множество T, включающее примеры из n классов, индекс Gini, т.е. gini(T), определяется по формуле:

где T - текущий узел, pj - вероятность класса j в узле T, n - количество классов.

Большое дерево не означает, что оно "подходящее"

Чем больше частных случаев описано в дереве решений, тем меньшее количество объектов попадает в каждый частный случай. Такие деревья называют "ветвистыми" или "кустистыми", они состоят из неоправданно большого числа узлов и ветвей, исходное множество разбивается на большое число подмножеств, состоящих из очень малого числа объектов. В результате "переполнения" таких деревьев их способность к обобщению уменьшается, и построенные модели не могут давать верные ответы.

В процессе построения дерева, чтобы его размеры не стали чрезмерно большими, используют специальные процедуры, которые позволяют создавать оптимальные деревья, так называемые деревья "подходящих размеров" (Breiman,1984).

Какой размер дерева может считаться оптимальным? Дерево должно быть достаточно сложным, чтобы учитывать информацию из исследуемого набора данных, но одновременно оно должно быть достаточно простым [39]. Другими словами, дерево должно использовать информацию, улучшающую качество модели, и игнорировать ту информацию, которая ее не улучшает.

Тут существует две возможные стратегии. Первая состоит в наращивании дерева до определенного размера в соответствии с параметрами, заданными пользователем. Определение этих параметров может основываться на опыте и интуиции аналитика, а также на некоторых "диагностических сообщениях" системы, конструирующей дерево решений.

Вторая стратегия состоит в использовании набора процедур, определяющих "подходящий размер" дерева, они разработаны Бриманом, Куилендом и др. в 1984 году. Однако, как отмечают авторы, нельзя сказать, что эти процедуры доступны начинающему пользователю.

Процедуры, которые используют для предотвращения создания чрезмерно больших деревьев, включают: сокращение дерева путем отсечения ветвей ; использование правил остановки обучения.

Следует отметить, что не все алгоритмы при конструировании дерева работают по одной схеме. Некоторые алгоритмы включают два отдельных последовательных этапа: построение дерева и его сокращение ; другие чередуют эти этапы в процессе своей работы для предотвращения наращивания внутренних узлов.

Остановка построения дерева

Рассмотрим правило остановки. Оно должно определить, является ли рассматриваемый узел внутренним узлом, при этом он будет разбиваться дальше, или же он является конечным узлом, т.е. узлом решением.

Остановка - такой момент в процессе построения дерева, когда следует прекратить дальнейшие ветвления.

Один из вариантов правил остановки - "ранняя остановка" (prepruning), она определяет целесообразность разбиения узла. Преимущество использования такого варианта - уменьшение времени на обучение модели. Однако здесь возникает риск снижения точности классификации. Поэтому рекомендуется "вместо остановки использовать отсечение" (Breiman, 1984).

Второй вариант остановки обучения - ограничение глубины дерева. В этом случае построение заканчивается, если достигнута заданная глубина.

Еще один вариант остановки - задание минимального количества примеров, которые будут содержаться в конечных узлах дерева. При этом варианте ветвления продолжаются до того момента, пока все конечные узлы дерева не будут чистыми или будут содержать не более чем заданное число объектов.

Существует еще ряд правил, но следует отметить, что ни одно из них не имеет большой практической ценности, а некоторые применимы лишь в отдельных случаях [35].

Сокращение дерева или отсечение ветвей

Решением проблемы слишком ветвистого дерева является его сокращение путем отсечения (pruning) некоторых ветвей.

Качество классификационной модели, построенной при помощи дерева решений, характеризуется двумя основными признаками: точностью распознавания и ошибкой.

Точность распознавания рассчитывается как отношение объектов, правильно классифицированных в процессе обучения, к общему количеству объектов набора данных, которые принимали участие в обучении.

Ошибка рассчитывается как отношение объектов, неправильно классифицированных в процессе обучения, к общему количеству объектов набора данных, которые принимали участие в обучении.

Отсечение ветвей или замену некоторых ветвей поддеревом следует проводить там, где эта процедура не приводит к возрастанию ошибки. Процесс проходит снизу вверх, т.е. является восходящим. Это более популярная процедура, чем использование правил остановки. Деревья, получаемые после отсечения некоторых ветвей, называют усеченными.

Если такое усеченное дерево все еще не является интуитивным и сложно для понимания, используют извлечение правил, которые объединяют в наборы для описания классов. Каждый путь от корня дерева до его вершины или листа дает одно правило. Условиями правила являются проверки на внутренних узлах дерева.