|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Методы принятия решений
Прямая (3) на рис. 4.4 - это прямая, соответствующая целевой функции  Она проходит между прямыми (1) и (4), задающими ограничения, и минимум достигается в точке А, через которую и проходит прямая (3). Следовательно, минимум равен
Она проходит между прямыми (1) и (4), задающими ограничения, и минимум достигается в точке А, через которую и проходит прямая (3). Следовательно, минимум равен  . Задача об оптимизации смеси полностью решена.
. Задача об оптимизации смеси полностью решена.
Двойственная задача, построенная по описанным выше правилам, имеет приведенный ниже вид (мы повторяем здесь и исходную задачу об оптимизации смеси, чтобы наглядно продемонстрировать технологию построения двойственной задачи):

Минимальное значение в прямой задаче, как и должно быть, равно максимальному значению в двойственной задаче, т.е. оба числа равны  . Интерпретация двойственных переменных:
. Интерпретация двойственных переменных: 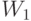 - "стоимость" единицы вещества
- "стоимость" единицы вещества  , а
, а 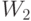 - "стоимость" единицы вещества Н, измеренные "по их вкладу" в целевую функцию. При этом
- "стоимость" единицы вещества Н, измеренные "по их вкладу" в целевую функцию. При этом 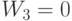 , поскольку ограничение на число калорий никак не участвует в формировании оптимального решения. Итак,
, поскольку ограничение на число калорий никак не участвует в формировании оптимального решения. Итак, 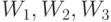 - это т.н. объективно обусловленные оценки (по Л.В. Канторовичу) ресурсов (веществ Т и Н, калорий).
- это т.н. объективно обусловленные оценки (по Л.В. Канторовичу) ресурсов (веществ Т и Н, калорий).
Планирование номенклатуры и объемов выпуска. Вернемся к организации производства. Предприятие может выпускать автоматические кухни (вид кастрюль), кофеварки и самовары. В табл.4.5 приведены данные о производственных мощностях, имеющихся на предприятии (в штуках изделий).
| Кухни | Кофеварки | Самовары | |
|---|---|---|---|
| Штамповка | 20000 | 30000 | 12000 |
| Отделка | 30000 | 10000 | 10000 |
| Сборка | 20000 | 12000 | 8000 |
| Объем выпуска |  |
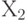 |
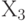 |
| Удельная прибыль (на одно изделие) | 15 | 12 | 14 |
При этом штамповка и отделка проводятся на одном и том же оборудовании. Оно позволяет штамповать за заданное время или 20000 кухонь, либо 30000 кофеварок, либо и то, и другое, не в меньшем количестве. А вот сборка проводится на отдельных участках.
Задача линейного программирования имеет вид:
 |
( 0) |
 |
( 1) |
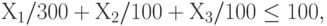 |
( 2) |
 |
( 3) |
 |
( 4) |
 |
( 5) |

Здесь:
(0) - обычное в экономике условие неотрицательности переменных,
(1) - ограничение по возможностям штамповки (выраженное для облегчения восприятия в процентах),
(2) - ограничение по возможностям отделки,
(3) - ограничение по сборке для кухонь,
(4) - то же для кофемолок,
(5) - то же для самоваров (как уже говорилось, все три вида изделий собираются на отдельных линиях).
Наконец, целевая функция  - общая прибыль предприятия.
- общая прибыль предприятия.
Заметим, что неравенство (3) вытекает из неравенства (1), а неравенство (4) - из (2). Поэтому неравенства (3) и (4) можно сразу отбросить.
Отметим сразу любопытный факт. Как будет установлено, в оптимальном плане  , т.е. самовары выпускать невыгодно.
, т.е. самовары выпускать невыгодно.
Методы решения задач линейного программирования. Методы решения задач линейного программирования относятся к вычислительной математике, а не к экономике. Однако экономисту полезно знать о свойствах интеллектуального инструмента, которым он пользуется.
С ростом мощности компьютеров необходимость применения изощренных методов снижается, поскольку во многих случаях время счета перестает быть лимитирующим фактором, поскольку весьма мало (доли секунд). Поэтому мы разберем лишь три метода.
Простой перебор. Возьмем некоторый многомерный параллелепипед, в котором лежит многогранник, задаваемый ограничениями. Как его построить? Например, если имеется ограничение типа  , то, очевидно,
, то, очевидно,  и
и  . Аналогичным образом от линейных ограничений общего вида можно перейти к ограничениям на отдельные переменные. Остается взять максимальные границы по каждой переменной. Если многогранник, задаваемый ограничениями, неограничен, как было в задаче о диете, можно похожим, но несколько более сложным образом выделить его "обращенную" к началу координат часть, содержащую решение, и заключить ее в многомерный параллелепипед.
. Аналогичным образом от линейных ограничений общего вида можно перейти к ограничениям на отдельные переменные. Остается взять максимальные границы по каждой переменной. Если многогранник, задаваемый ограничениями, неограничен, как было в задаче о диете, можно похожим, но несколько более сложным образом выделить его "обращенную" к началу координат часть, содержащую решение, и заключить ее в многомерный параллелепипед.
Проведем перебор точек параллелепипеда с шагом  последовательно при
последовательно при  , вычисляя значения целевой функции и проверяя наличие ограничений. Из всех точек, удовлетворяющих ограничениям, возьмем ту, в которой целевая функция максимальна. Решение найдено! (Более строго выражаясь, найдено с точностью до
, вычисляя значения целевой функции и проверяя наличие ограничений. Из всех точек, удовлетворяющих ограничениям, возьмем ту, в которой целевая функция максимальна. Решение найдено! (Более строго выражаясь, найдено с точностью до  .)
.)
Направленный перебор. Начнем с точки, удовлетворяющей ограничениям (ее можно найти простым перебором). Будем последовательно (или случайно - т.н. метод случайного поиска) менять ее координаты на определенную величину  , каждый раз в точку с более высоким значением целевой функции. Если выйдем на плоскость ограничения, будем двигаться по ней (находя одну из координат по уравнению ограничения). Затем движение по ребру (когда два ограничения-неравенства переходят в равенства)… Остановка - в вершине линейного многогранника. Решение найдено! (Более строго выражаясь, найдено с точностью до
, каждый раз в точку с более высоким значением целевой функции. Если выйдем на плоскость ограничения, будем двигаться по ней (находя одну из координат по уравнению ограничения). Затем движение по ребру (когда два ограничения-неравенства переходят в равенства)… Остановка - в вершине линейного многогранника. Решение найдено! (Более строго выражаясь, найдено с точностью до  ; если необходимо, в окрестности найденного решения проводим направленный перебор с шагом
; если необходимо, в окрестности найденного решения проводим направленный перебор с шагом  и т.д.)
и т.д.)
Симплекс-метод. Этот один из первых специализированных методов оптимизации, нацеленный на решение задач линейного программирования, в то время как методы простого и направленного перебора могут быть применены для решения практически любой задачи оптимизации. Он был предложен американцем Г. Данцигом в 1951 г. Симплекс-метод состоит в продвижении по выпуклому многограннику ограничений от вершины к вершине, при котором на каждом шаге значение целевой функции улучшается до тех пор, пока не будет достигнут оптимум..
Рассмотрим задачу линейного программирования, сформулированную выше при рассмотрении оптимизации номенклатуры и объемов выпуска:

Неотрицательность переменных не будем специально указывать, поскольку в задачах линейного программирования это предположение всегда принимается.
В соответствии с симплекс-методом введем т.н. "свободные переменные"  , соответствующие недоиспользованным мощностям, т.е. перейдем к системе уравнений:
, соответствующие недоиспользованным мощностям, т.е. перейдем к системе уравнений:

У этой системы имеется очевидное решение, соответствующее вершине многогранника допустимых значений переменных:
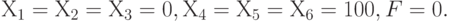
В терминах исходной задачи это значит, что ничего не надо выпускать. Такое решение приемлемо только на период летних отпусков.
Выбираем переменную, которая входит в целевую функцию  с самым большим положительным коэффициентом. Это
с самым большим положительным коэффициентом. Это 
Сравниваем частные от деления свободных членов в первых трех уравнениях на коэффициенты при только что выбранной переменной  :
:

Выбираем строку, которой соответствует минимальное из всех положительных отношений. В рассматриваемом примере - это первая строка, которой соответствует отношение 20000.
Умножим первую строку на 200, чтобы получить  с единичным коэффициентом:
с единичным коэффициентом:

Затем умножим вновь полученную строку на (-1/300) и сложим со второй строкой, получим

Ту же преобразованную первую строку умножим на (-15) и сложим со строкой, в правой части которой стоит  , получим:
, получим:

В результате система уравнений преобразуется к виду, в котором переменная Х1 входит только в первое уравнение:
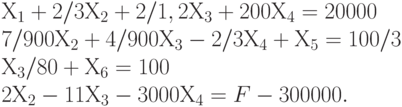
Очевидно, у новой системы имеется улучшенное по сравнению с исходным решение, соответствующее вершине в шестимерном пространстве:

В терминах исходной задачи это значит, что надо выпускать только кухни. Такое решение приемлемо, если допустимо выпускать только один вид продукции.
Повторим описанную выше операцию. В строке с  имеется еще один положительный коэффициент - при
имеется еще один положительный коэффициент - при 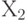 (если бы положительных коэффициентов было несколько - мы взяли бы максимальный из них). На основе коэффициентов при
(если бы положительных коэффициентов было несколько - мы взяли бы максимальный из них). На основе коэффициентов при 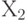 (а не при
(а не при  , как в первый раз) образуем частные от деления соответствующих свободных членов на эти коэффициенты:
, как в первый раз) образуем частные от деления соответствующих свободных членов на эти коэффициенты:

Таким образом, нужно выбрать вторую строку, для которой имеем наименьшее положительное отношение 30000/7. Вторую строку умножим на 900/7 (чтобы коэффициент при 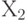 равнялся 1). Затем добавим обновленную строку ко всем строкам, содержащим
равнялся 1). Затем добавим обновленную строку ко всем строкам, содержащим 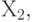 предварительно умножив их на подходящие числа, т.е. такие, чтобы все коэффициенты при
предварительно умножив их на подходящие числа, т.е. такие, чтобы все коэффициенты при 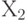 стали бы после сложения равны 0, за исключением коэффициента второй строки, который уже стал равняться 1. Получим систему уравнений:
стали бы после сложения равны 0, за исключением коэффициента второй строки, который уже стал равняться 1. Получим систему уравнений:

Поскольку все переменные неотрицательны, то из последнего уравнения следует, что прибыль F достигает своего максимального значения, равного 308571, при 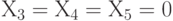 . Из остальных уравнений следует, что при этом
. Из остальных уравнений следует, что при этом  . Поскольку в строке с
. Поскольку в строке с  не осталось ни одного положительного коэффициента при переменных, то алгоритм симплекс-метода закончил свою работу, оптимальное решение найдено.
не осталось ни одного положительного коэффициента при переменных, то алгоритм симплекс-метода закончил свою работу, оптимальное решение найдено.
Практические рекомендации таковы: надо выпустить 17143 кухни, вчетверо меньше, т.е. 4286 кофемолок, самоваров не выпускать вообще. При этом прибыль будет максимальной и равной 308571. Все производственное оборудование будет полностью загружено, за исключением линии по сборке самоваров.
Транспортная задача. Различные технико-экономические и экономические задачи производственного менеджмента, от оптимальной загрузки станка и раскройки стального листа или полотна ткани до анализа межотраслевого баланса и оценки темпов роста экономики страны в целом, приводят к необходимости решения тех или иных задач линейного программирования. В книге [4.3] приведен обширный перечень публикаций, посвященный многочисленным применениям линейного программирования в металлургии, угольной, химической, нефтяной, бумажной и прочих отраслях промышленности, в проблемах транспорта и связи, планирования производства, конструирования и хранения продукции, сельском хозяйстве, в научных исследованиях, в том числе экономических, и даже при регулировании уличного движения.
В качестве очередного примера рассмотрим т.н. транспортную задачу. Имеются склады, запасы на которых известны. Известны потребители и объемы их потребностей. Необходимо доставить товар со складов потребителям. Можно по-разному организовать "прикрепление" потребителей к складам, т.е. установить, с какого склада какому потребителю и сколько вести. Кроме того, известна стоимость доставки единицы товара с определенного склада определенному потребителю. Требуется минимизировать издержки по перевозке.
Например, может идти речь о перевозке песка - сырья для производства кирпичей. В Москву песок обычно доставляется самым дешевым транспортом - водным. Поэтому в качестве складов можно рассматривать порты, а в качестве запасов - их суточную пропускную способность. Потребителями являются кирпичные заводы, а их потребности определяются суточным производством (в соответствии с имеющимися заказами). Для доставки необходимо загрузить автотранспорт, проехать по определенному маршруту и разгрузить его. Стоимость этих операций рассчитывается по известным правилам, на которых не имеет смысла останавливаться.

