|
Есть такие задания, и они никак не принимаются. Притом ошибки только по этим заданиям, в какой бы последовательности я их не заполнял. Как их заполнять??? Инструкций в заданиях нет. Там через запятые, подряд как число, через пробел, или надо текст весь писать через запятую или точку? Задание: Пронумеруйте шаги Создание имени путем выделения ячеек на листе: |
Решение оптимизационных задач методом поиска решения
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К классу задач линейного программирования (ЛП) относятся такие задачи однокритериальной оптимизации, в которых переменные являются непрерывными и неотрицательными, целевая функция является линейной функцией своих аргументов, а ограничения могут быть представлены в форме линейных неравенств и равенств.
Задача линейного программирования в общем случае формулируется следующим образом:
Определить максимум (минимум) целевой функции Fmax(min) при заданной системе ограничений (2) и граничных условий (3):
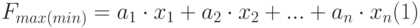
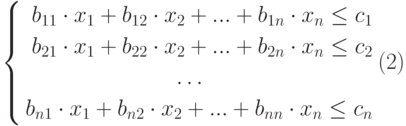
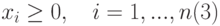
Надстройка Поиск решения является инструментом оптимизации. С помощью этой надстройки можно найти оптимальное или заданное значение некоторой ячейки путем подбора значений нескольких ячеек, удовлетворив нескольким граничным условиям.
Целевая ячейка – это ячейка, для которой нужно найти максимальное, минимальное или заданное значения.
Изменяемые ячейки – это ячейки, от которых зависит значение целевой ячейки. Целевая ячейка должна содержать формулу, прямо или косвенно зависящую от изменяемых ячеек. Поиск решения подбирает значения изменяемых ячеек до тех пор, пока не будет найдено решение.
Ограничение – это условие, накладываемое на некоторую ячейку. Ограничения могут быть наложены на любые ячейки таблицы, включая целевую ячейку и изменяемые ячейки.
Чтобы запустить процедуру поиска решения, надо:
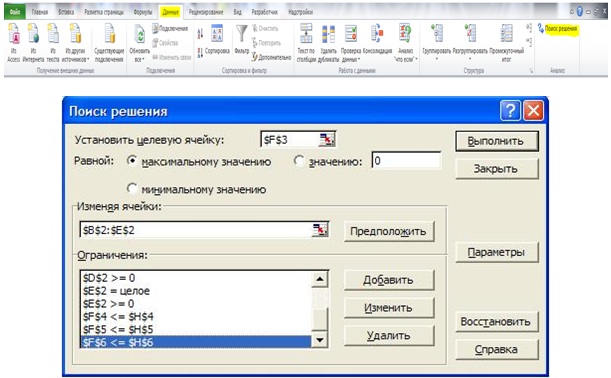
- В меню Данные выбрать команду Поиск решения. Откроется диалоговое окно Поиск решения (рис. 12. рис. 12.11).
- В поле Установить целевую ячейку ввести ссылку на ячейку, в которой нужно получить максимальное, минимальное или заданное значения.
- В поле Изменяя ячейки ввести ссылки на изменяемые ячейки. (Если щелкнуть по кнопке Предположить, то Поиск решения самостоятельно определит изменяемые ячейки).
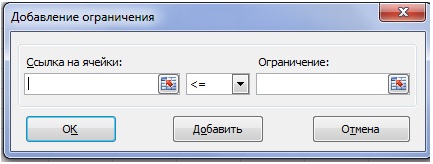
- Для задания ограничений щелкнуть по кнопке Добавить.
- В открывшемся диалоговом окне следует: (рис. 12.2 рис. 12.2)
- в поле Ссылка на ячейку ввести ссылку на ячейку, содержащую формулу, которая определяет ограничение; формула должна прямо или косвенно зависеть от одной или нескольких изменяемых ячеек;
- во втором поле выбрать оператор ограничения (>,<,= и т.д.);
- в поле Ограничение ввести значение ограничения.
- Для задания следующего ограничения щелкнуть по кнопке Добавить и повторить операции пункта 5.
- Когда все ограничения будут заданы, щелкнуть по кнопке ОК, чтобы вернуться в диалоговое окно Поиск решения.
- Изменять и удалять ограничения можно с помощью кнопок Изменить и Удалить.
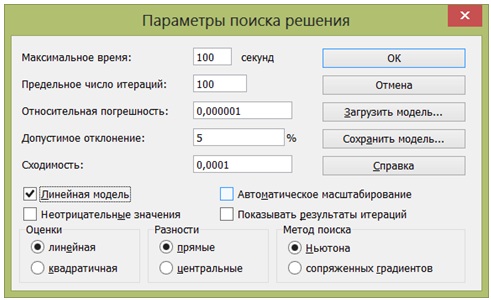
- С помощью кнопки Параметры можно задать: максимальное время решения; предельное число итераций; относительную погрешность; допустимое отклонение; сходимость; метод поиска.
Если известно, что решаемая задача линейная (т.е. зависимости между переменными линейны), то следует включить режим Линейная модель: процесс решения значительно ускорится.
Для возврата в диалоговое окно Поиск решения щелкнуть по кнопке ОК.
Для инициализации процедуры поиска решения щелкнуть по кнопке Выполнить. Полученные результаты будут выведены на рабочий лист.
После завершения процедуры решения в диалоговом окне Результаты поиска решения можно выполнить один из следующих вариантов:
- сохранить найденное решение или восстановить исходные значения на рабочем листе;
- сохранить параметры поиска решения в виде модели;
- сохранить решение в виде сценария;
- просмотреть любой из встроенных отчетов.
Текущие установочные параметры для поиска решения можно сохранить в виде модели. Для этого надо в диалоговом окне Параметры поиска решения щелкнуть по кнопке Сохранить модель и указать на рабочем листе область для сохранения модели (можно указать только верхнюю ячейку области).
При сохранении модели запоминаются целевая ячейка, изменяемые ячейки, ограничения и параметры поиска решения.
Чтобы впоследствии загрузить модель, надо щелкнуть по кнопке Загрузить модель в диалоговом окне Параметры поиска решения. (Диалоговое окно Параметры поиска решения открывается при щелчке по кнопке Параметры в диалоговом окне команды Сервис > Поиск решения).
Найденные решения (значения изменяемых ячеек) можно сохранить в качестве сценария. Для этого нужно:
- В диалоговом окне Результаты поиска решения выбрать Сохранить сценарий.
- В поле Название сценария ввести имя сценария. Просмотреть сценарии можно с помощью команды Данные > Работа с данными > Анализ что-если > Диспетчер сценариев > Сценарии.
С помощью программы Поиск решения можно создать три типа отчетов по результатам, полученным при успешном завершении процедуры решения.
Каждый отчет создается на отдельном листе текущей рабочей книги.
Для создания отчета надо в диалоговом окне Результаты поиска решения выбрать нужный тип отчета в поле Тип отчета. Можно выбрать сразу несколько типов (при выделении нескольких строк используется клавиша <Ctrl>).
Типы отчетов:
- Результаты – отчет содержит целевую ячейку, список изменяемых ячеек, их исходные и конечные значения, ограничения и сведения о них.
- Устойчивость – отчет содержит сведения о степени зависимости модели от изменений величин, входящих в формулы, применяемые в задаче (формулы модели и формулы ограничений).
- Пределы – выводится целевая ячейка и ее значение, а также список изменяемых ячеек, их значений, нижних и верхних пределов и целевых результатов.
Рассмотрим применение процессора Excel для решения ЗЛП на примерах.
Задача 1. Планирование производства
Модель линейного программирования дает возможность определить наиболее выгодную производственную программу выпуска нескольких видов продукции при заданных ограничениях на ресурсы.
МП выпускает товары х1,х2,х3,х4, получая от реализации каждого прибыль в 60,70,120,130 руб. соответственно. Затраты на производство приведены в таблице.
Определить:
- Максимум прибыли в зависимости от оптимального распределения затрат.
- Минимум ресурсов, необходимых для получения максимальной прибыли.
Решение задачи средствами Excel состоит из 4 этапов:
- Создание математической модели задачи ЛП.
- Создание формы для ввода условий задачи, ввод в неё исходных данных и зависимостей из математической модели.
- Ввод данных из формы в окно Excel Поиск решения из меню Данные.
- Задание параметров поиска и решение задачи.
Создание математической модели задачи
Составим математическую модель процесса по описанию задачи:
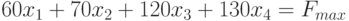 - целевая функция прибыли.
- целевая функция прибыли.
Ограничения модели:
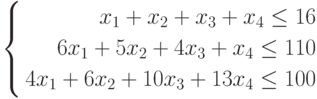
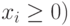 - граничные условия модели, так как количество производимых товаров не может быть отрицательной величиной.
- граничные условия модели, так как количество производимых товаров не может быть отрицательной величиной.
Для решения данной задачи c помощью программы MS Excel создадим новую книгу с именем Линейное программирование и изменим имя ее первого рабочего листа на Задача о производстве.
Создание формы
- Составление формы в виде:
| A | B | C | D | E | F | G | H | |
|---|---|---|---|---|---|---|---|---|
| 1 | Переменная | х7 | х2 | x3 | х4 | Формула | Знак | Св.член |
| 2 | Значение | |||||||
| 3 | Коэф. ЦФ | 60 | 70 | 120 | 130 | =СУММПРОИЗВ(В$2:Е$2;В3:Е3) | Max | |
| 4 | Трудовые | 1 | 1 | 1 | 1 | =СУММПРОИЗВ(В$2:Е$2;В4:Е4) |  |
16 |
| 5 | Сырьевые | 6 | 5 | 4 | 1 | =СУММПРОИЗВ(В$2:Е$2;В5:Е5) |  |
110 |
| 6 | Финансы | 4 | 6 | 10 | 13 | =СУММПРОИЗВ(В$2:Е$2;В6:Е6) |  |
100 |
- Запись в ячейки В3:Е3 коэффициентов целевой функции F (1), в В4:Е6 коэффициентов из системы ограничений (2) и в ячейки Н4:Н6 – свободных членов из системы (2).
- Ввод формул с помощью fx – Мастера функций.
Для ввода формулы в целевую ячейку (целевой функции): щелкнуть левой клавишей мыши по ячейке F3, затем по значку Мастера функций fx на панели инструментов, в появившемся окне "Мастер функций, Шаг 1" выбрать категорию "Математические", далее выбрать функцию СУММПРОИЗВ, нажать клавишу ОК, в окне "Мастер функций Шаг 2" в поле Массив 1 ввести с клавиатуры В2:Е2 (ячейки, в которых будут варьироваться х1..х4), в поле Массив 2 ввести В3:Е3 (коэффициенты целевой функции ЦФ).
Примечание. Можно вводить В2:Е2 не с клавиатуры, а поставить курсор в окно Массив 1, а затем протащить курсор при нажатой левой клавише мыши по ячейкам В2:Е2, имена ячеек сами запишутся в окно. Аналогично поступить с полем Массив 2.
Нажать клавишу ОК, в ячейку F3 запишется формула 60х1+70х2+120х3+ 130х4 в виде СУММПРОИЗВ(В2:Е2;В3:Е3).
Чтобы не вводить формулы в другие ячейки, необходимо изменить тип адресации для ячеек В2:Е2 с относительной на абсолютную $B$2:$E$2, установив курсор перед нужным адресом B2 и нажав функциональную клавишу F4, затем повторить эти действия для адреса E2. Формула примет следующий вид:
СУММПРОИЗВ($В$2:$Е$2;В3:Е3)
После внесенных изменений необходимо скопировать формулу в ячейки F4:F6 c помощью маркера заполнения. Для этого необходимо выделить ячейку F3, содержащую нужную формулу, установить указатель мыши на черный квадратик в правом нижнем углу ячейки (он примет форму черного крестика) и протащить с помощью левой кнопки мыши на весь требуемый диапазон.
В результате копирования мы увидим следующие формулы:
- в ячейке F4 – СУММПРОИЗВ($В$2:$Е$2;В4:Е4),
- в ячейке F5 – СУММПРОИЗВ($В$2:$Е$2;В5:Е5),
- в ячейке F6 – СУММПРОИЗВ($В$2:$Е$2;В6:Е6).
Заполнение окна Поиск решения
Выбрать в пункте меню Данные команду Поиск решения, поставить курсор в поле целевой функции, выделить ячейку F3 в форме (или ввести F3 с клавиатуры), поставить переключатель в положение "Максимальному значению" (см. рис. 12.1 рис. 12.1). В поле "Изменяя ячейки" ввести $В$2:$Е$2(с клавиатуры или протащив мышью).
Нажать клавишу "Добавить", в окне "Добавление ограничения" в поле "Ссылка на ячейку" ввести F4, выбрать через "стрелка вниз" знак " ", в поле справа ввести Н4 (рис. 12.
рис.
12.2).
", в поле справа ввести Н4 (рис. 12.
рис.
12.2).
Аналогично через "Добавить" ввести 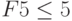 ,
, 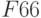 для системы ограничений (2), а также
для системы ограничений (2), а также 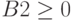 ,
, 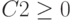 ,
, 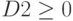 и
и 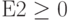 .
.
Также необходимо добавить ограничения для получения целочисленных величин по количеству товаров: B2=цел, C2=цел, D2=цел и Е2=цел.
После ввода последнего граничного условия вместо "Добавить" нажать клавишу ОК, появится окно "Поиск решения".
Для изменения или удаления ограничений и граничных условий используются клавиши Изменить, Удалить.
Параметры поиска
В окне "Поиск решения" нажать клавишу "Параметры", выбрать по умолчанию Максимальное время – 100 с, число итераций – 100 (для большинства задач это количество просчётов подходит с большим запасом), установить флажок в строке "Линейная модель", нажать ОК, в появившемся окне Поиск Решения нажать Выполнить (рис. 12. рис. 12.3).
Результаты поиска решения с таблицей результатов:
| A | B | C | D | E | F | G | H | |
|---|---|---|---|---|---|---|---|---|
| 1 | Переменная | X1 | X2 | X3 | X4 | Формула | Знак | Св.член |
| 2 | Значение | 10 | 0 | 6 | 0 | |||
| 3 | Коэф. ЦФ | 60 | 70 | 120 | 130 | 1320 | Max | |
| 4 | Трудовые | 1 | 1 | 1 | 1 | 16 |  |
16 |
| 5 | Сырьевые | 6 | 5 | 4 | 1 | 84 |  |
110 |
| 6 | Финансы | 4 | 6 | 10 | 13 | 100 |  |
100 |
Таким образом оптимальный план Х(Х1,Х2,Х3,Х4)=(10,0,6,0) при минимальном использовании ресурсов
- Трудовые – 16 (У1)
- Сырьевые – 84 (У2)
- Финансы – 100 (У3)
даёт максимум прибыли F в 1320 руб.
Вывод: Максимальная прибыль F в 1320 руб. получается при выпуске только товаров Х1 и Х3 в количестве 10 и 6 штук соответственно, товары Х3 и Х4 выпускать не нужно (это приведёт к снижению прибыли). Трудовые (У1) и финансовые (У3) ресурсы используются полностью, по сырьевым ресурсам (У2) есть запас в 110-84=26 ед.
Кроме того, это означает, что изменение трудовых (y1) и финансовых (y3) ресурсов приведёт к изменению прибыли F, а изменение сырьевых ресурсов (y2) – нет.
Разности между плановыми ресурсами и использованными являются двойственными переменными y1, y2 и y3 сопряжённой задачи линейного программирования. В данном случае y1=y3=0, а y2=26 ед. Таким образом, ресурс y2 можно уменьшить на 26 ед., тогда план по сырью тоже будет оптимальным.
Задача 2. Задача об оптимальной диете
Имеется n видов продуктов питания, в которых содержится m типов питательных веществ (белки, жиры, углеводы). В одной весовой единице продукта i-го типа  содержится аi единиц питательного вещества j-го вида
содержится аi единиц питательного вещества j-го вида  . Известна минимальная суточная потребность b j (j \in {1,2,..., т}) человека в каждом из видов питательных веществ. Задана калорийность сi одной весовой единицы i-го продукта (i принадлежит {1, 2, ..., n}).
. Известна минимальная суточная потребность b j (j \in {1,2,..., т}) человека в каждом из видов питательных веществ. Задана калорийность сi одной весовой единицы i-го продукта (i принадлежит {1, 2, ..., n}).
Требуется определить оптимальный состав рациона продуктов, такой, чтобы каждое питательное вещество содержалось в нем в необходимом количестве, обеспечивающем суточную потребность человека, и при этом суммарная калорийность рациона была минимальной.
Ведем в рассмотрение следующие переменные: х – весовое количество продукта питания i-го типа в суточном рационе.
Тогда в общем случае математическая постановка задачи об оптимальной диете может быть сформулирована следующим образом:
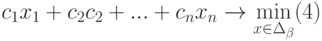
где множество допустимых альтернатив 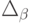 формируется следующей системой ограничений типа неравенств:
формируется следующей системой ограничений типа неравенств:
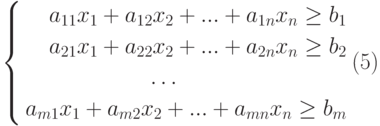
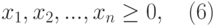
Для решения задачи об оптимальной диете с помощью программы MS Excel необходимо задать конкретные значения параметрам исходной задачи.
Для определенности предположим, что в качестве исходных типов продуктов рассматриваются: хлеб, мясо, сыр, бананы, огурцы, помидоры, виноград (n = 7), а в качестве питательных веществ рассматриваются белки, жиры, углеводы (m = 3).
Калорийность одной весовой единицы каждого из продуктов следующая:с1 = 2060,с2= 2430,с3= 3600,с4= 890,с5= 140,с6= 230, с7 = 650. Содержание питательных веществ в каждом из продуктов может быть задано в форме нижеприведенной таблицы.
Минимальная суточная потребность в питательных веществах следующая: в белках b 1 = 100, в жирах b 2= 70, в углеводах b3 = 400.
Для решения данной задачи c помощью программы MS Excel создадим новую книгу с именем Линейное программирование и изменим имя ее второго рабочего листа на Задача о диете.
| Продукты/питательные вещества | Хлеб ржаной | Мясо баранина | Сыр "Российский" | Банан | Огурцы | Помидоры | Виноград |
|---|---|---|---|---|---|---|---|
| Белки | 61 | 220 | 230 | 15 | 8 | 11 | 6 |
| Жиры | 12 | 172 | 290 | 1 | 1 | 2 | 2 |
| Углеводы | 420 | 0 | 0 | 212 | 26 | 38 | 155 |
Создание математической модели задачи
Составим математическую модель процесса по описанию задачи:
 – целевая функция (суммарная калорийность продуктов).
– целевая функция (суммарная калорийность продуктов).
Ограничения модели:
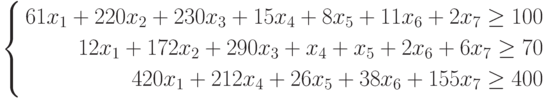
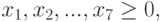 – граничные условия
– граничные условия
Создание формы
Для решения поставленной задачи выполним следующие подготовительные действия:
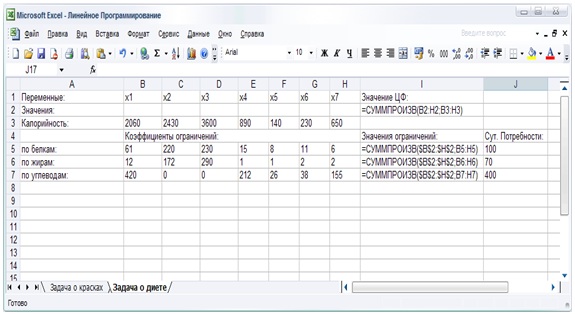
- Внесем необходимые надписи в ячейки A1:I1, A2:A7, B4, I4, J4.
- В ячейки ВЗ:НЗ введем значения коэффициентов целевой функции: с1 = 2060, с2 = 2430, с3 = 3600, с4 = 890, с5 = 140, с6 = 230, с7 = 650.
- В ячейку I2 введем формулу: =СУММПРОИЗВ( b2:Н2;B3:H3), которая представляет целевую функцию (4).
- В ячейки В5:Н7 введем значения коэффициентов ограничений, взятых из таблицы.
- В ячейки J5:J7 введем значения правых частей ограничений, соответствующих минимальной суточной потребности в питательных веществах: в белках b 1=100, жирах b 2= 70 и углеводах b3 = 400.
- В ячейку I5 введем формулу: =СУММПРОИЗВ($B$2:$H$2;В5:Н5), которая представляет левую часть первого ограничения (5).
- Скопируем формулу, введенную в ячейку I5, в ячейки I6 и I7.
- Внешний вид рабочего листа MS Office Excel с исходными данными для решения задачи об оптимальном рационе питания имеет следующий вид (pиc. 12.4).
Для отображения формул в ячейках рабочего листа необходимо выполнить команду меню: Формулы и на панели инструментов в группе Зависимости формул выбрать Показать формулы.
Заполнение окна Поиск решения
Для дальнейшего решения задачи следует вызвать мастер поиска решения, для чего необходимо выполнить операцию: Данные > Поиск решения...
После появления диалогового окна Поиск решения следует выполнить следующие действия:
- В поле с именем Установить целевую ячейку: ввести абсолютный адрес ячейки $I$2.
- Для группы Равной: выбрать вариант поиска решения – минимальному значению.
- В поле с именем Изменяя ячейки: ввести абсолютный адрес ячеек $B$2:$H$2.
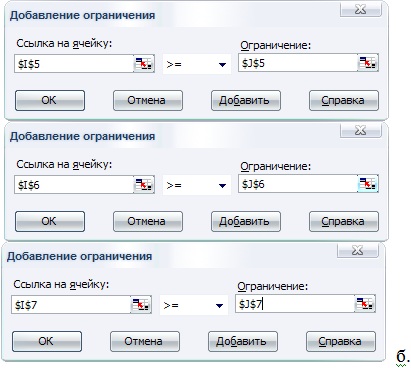
- Добавить 3 ограничения, представляющие минимальные суточные потребности в питательных веществах. С этой целью выполнить следующие действия:
- для задания первого ограничения в исходном диалоговом окне Поиск решения нажать кнопку с надписью Добавить (рис. 12.5 рис. 12.5, а);
- в появившемся дополнительном окне выбрать ячейку $I$5, которая должна отобразиться в поле с именем Ссылка на ячейку;
- в качестве знака ограничения из выпадающего списка выбрать нестрогое неравенство " ";
- в качестве значения правой части ограничения выбрать ячейку $J$5;
- для добавления первого ограничения в дополнительном окне нажать кнопку с надписью Добавить;
- аналогичным образом задать оставшиеся два ограничения (рис. 12.5 рис. 12.5, б).
- Добавить ограничение на допустимые значения переменных. С этой целью выполнить следующие действия:
- в исходном диалоговом окне Поиск решения нажать кнопку с надписью Добавить;
- в появившемся дополнительном окне выбрать диапазон ячеек $В$2:$Н$2, который должен отобразиться в поле с именем Ссылка на ячейку;
- в качестве знака ограничения из выпадающего списка выбрать нестрогое неравенство "
 ";
"; - в качестве значения правой части ограничения в поле с именем Ограничение: ввести значение 0;
- для добавления ограничения в дополнительном окне нажать кнопку с надписью Добавить (рис. 12.6 рис. 12.6, а).
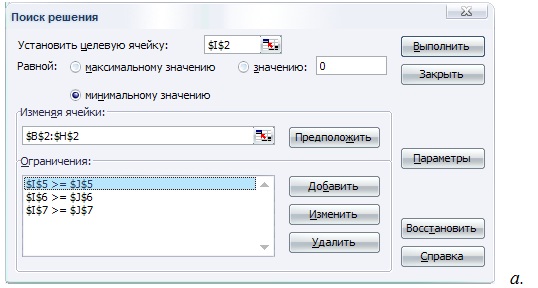
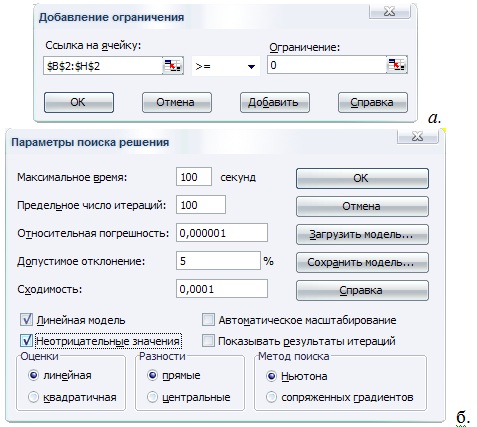
Рис. 12.6. Ограничения на значения переменных и параметры мастера поиска решения для задачи об оптимальной диете
Параметры
В окне "Поиск решения" нажать клавишу "Параметры", выбрать "Поиск решения Линейных задач симплекс-методом", нажать ОК, затем нажать Найти Решение (рис. 12.6 рис. 12.6, б).
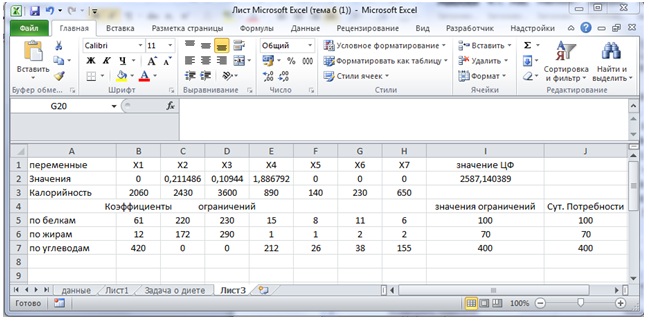
После задания ограничений и целевой функции можно приступить к поиску численного решения, для чего следует нажать кнопку Выполнить. После выполнения расчетов программой MS Excel будет получено количественное решение, которое имеет вид, представленный на рис. 12. рис. 12.7.
Результатом решения задачи об оптимальной диете являются найденные оптимальные значения переменных: х1 = 0, х2 = 0,211, 3 = 0,109, х4= 1,887, х5 = 0, х6 = 0, х7 = 0, которым соответствует значение целевой функции: fопт= 2587,140. При выполнении расчетов для ячеек В2:I2 был выбран числовой формат с 3 знаками после запятой.
Анализ найденного решения показывает, что для удовлетворения суточной потребности в питательных веществах (белки, жиры, углеводы) следует использовать 211 г мяса баранины, 109 г сыра и 1887 г бананов, совсем отказавшись от хлеба, огурцов, помидоров и винограда. При этом общая калорийность найденной оптимальной диеты будет приближенно равна 2590 ккал, что вполне соответствует малоактивному образу жизни без серьезных физических нагрузок. Напомним, что согласно медицинским данным, энергетические затраты работников интеллектуального труда (юристы, бухгалтера, врачи, педагоги) лежат в пределах 3000 ккал.
ЗАДАНИЕ
- Составить математическую модель задачи линейного программирования.
- Решить задачу линейного программирования в Excel с помощью Поиска решения.
- Сохранить в виде модели установочные параметры.
Вариант 1.
Предприятие легкой промышленности выпускает две модели машин, причем каждая модель производится на отдельной технологической линии. Суточный объем производства первой линии – 80 изделий, второй линии – 85 изделий. На машину первой модели расходуются 12 однотипных элементов электронных схем, на машину второй модели – 6 таких же элементов. Максимальный суточный запас используемых элементов равен 800 единицам. Прибыль от реализации одной машины первой и второй моделей равна $30 и $40 соответственно. Определить оптимальный суточный объем производства первой и второй моделей.
Вариант 2.
Процесс изготовления двух видов промышленных изделий состоит в последовательной обработке каждого из них на трех приборах. Время использования этих приборов для производства данных изделий ограничено 10 ч. в сутки. Найти оптимальный объем производства изделий каждого вида.

Вариант 3.
Фирма имеет возможность рекламировать свою продукции, используя местные радио- и телевизионную сеть. Затраты на рекламу в бюджете фирмы ограничены $1000 в месяц. Каждая минута радиорекламы обходится в $5, а минута телерекламы – в $100. Фирма хотела бы использовать радиосеть, по крайней мере, в два раза чаще, чем сеть телевидения. Опыт прошлых лет показал, что объем сбыта, который обеспечивает каждая минута телерекламы, в 25 раз больше сбыта, обеспечиваемого одной минутой радиорекламы. Определить оптимальное распределение ежемесячно отпускаемых средств между радио- и телерекламой.
Вариант 4.
Фирма производит два вида продукции – А и B. Объем сбыта продукции вида A составляет не менее 70% общего объема реализации продукции обоих видов. Для изготовления продукции А и В используется одно и то же сырье, суточный запас которого ограничен величиной 120 кг. Расход сырья на единицу продукции A составляет 3 кг, а на единицу продукции В – 5 кг. Цены продукции А и В равны $20 и $60 соответственно. Определить оптимальное распределение сырья для изготовления продукции А и В.
Вариант 5.
Фирма выпускает женские шляпы двух фасонов. Трудоемкость изготовления шляпы фасона 1 вдвое выше трудоемкости изготовления шляпы фасона 2. Если бы фирма выпускала только шляпы фасона 1, суточный объем производства мог бы составить 60 шляп. Суточный объем сбыта шляп обоих фасонов ограничен диапазоном от 50 до 100 штук. Прибыль от продажи шляпы фасона 1 равна $6, а фасона 2 – $7. Определить какое количество шляп каждого фасона следует изготавливать, чтобы максимизировать прибыль.
Вариант 6.
Изделия четырех типов проходят последовательную обработку на двух станках. Время обработки одного изделия каждого типа на каждом из станков:

Затраты на производство одного изделия каждого типа определяются как величины, прямо пропорциональные времени использования станков (в машино-часах). Стоимость машино-часа составляет $10 и $15 для станка 1 и 2 соответственно. Допустимое время для использования станков для обработки изделий всех типов ограничено следующими значениями: 500 машино-часов – для станка 1 и 380 машино-часов для станка 2. Цены изделий типов 1,2,3 и 4 равны $65, $70, $55 и $45 соответственно. Составить план производства, максимизирующий чистую прибыль.
Вариант 7.
Завод выпускает изделия трех моделей (I, II III) Для их изготовления используется два вида ресурсов (А и В), запасы которых составляют – 5000 и 6000 единиц. Расходы ресурсов на одно изделие каждой модели:

Трудоемкость изготовления модели I вдвое больше, чем изделия модели II, и втрое больше, чем изделие модели III. Численность рабочих завода позволяет выпускать 1500 изделий I. Анализ условий сбыта показывает, что минимальный спрос на продукцию завода составляет 200, 200 и 150 изделий моделей I,II и III соответственно. Однако соотношение выпуска изделий моделей I,II и III должно быть равно 3:2:5. Удельная прибыль от реализации изделий моделей I,II и III составляет $30, $20 и $50 соответственно. Определить выпуск изделий, максимизирующий прибыль.
Вариант 8.
Требуется распределить имеющиеся денежные средства по четырем альтернативным вариантам. Игра имеет три исхода. Ниже приведены размеры выигрыша (или проигрыша) на каждый доллар, вложенный в соответствующий альтернативный вариант, для любого из трех исходов. У игрока имеется $500, причем, использовать в игре их можно только один раз. Точный исход игры заранее неизвестен, и, учитывая эту неопределенность, игрок решил распределить деньги так, чтобы максимизировать максимальную отдачу от этой суммы.

Вариант 9.
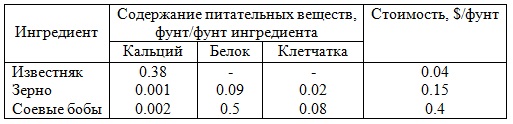
Бройлерное хозяйство птицеводческой фермы насчитывает 80000 цыплят, которые выращиваются до 8-недельного возраста и после соответствующей обработки поступают в продажу. Хотя недельный рацион цыплят зависит от их возраста, в дальнейшем будем считать, что в среднем (за 8 недель) он составляет 1 фунт.
Для того чтобы цыплята достигли к восьмой неделе необходимых весовых кондиций, кормовой рацион должен удовлетворять определенным требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов или ингредиентов. Ограничим наше рассмотрение только тремя ингредиентами: известняком, зерном и соевыми бобами. Ниже приведены данные, характеризующие содержание (по весу) питательных веществ в каждом из ингредиентов и удельную стоимость каждого ингредиента.

Смесь должна содержать:
- не менее 0.8%, но не более 1.2% кальция;
- не менее 22% белка;
- не более 5% клетчатки.
Необходимо определить количество каждого из трех ингредиентов, образующих смесь минимальной стоимости при соблюдении требований к общему расходу кормовой смеси и ее питательности.
Вариант 10.
Имеется n видов продуктов питания, в которых содержится m типов питательных веществ (белки, жиры, углеводы). В одной весовой единице продукта i-го типа  содержится аi единиц питательного вещества j-го вида
содержится аi единиц питательного вещества j-го вида  . Известна минимальная суточная потребность b j
. Известна минимальная суточная потребность b j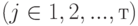 человека в каждом из видов питательных веществ. Задана калорийность сi одной весовой единицы i-го продукта (i принадлежит {1, 2, ..., n}). Требуется определить оптимальный состав рациона продуктов, такой, чтобы каждое питательное вещество содержалось в нем в необходимом количестве, обеспечивающем суточную потребность человека, и при этом суммарная калорийность рациона была минимальной.
человека в каждом из видов питательных веществ. Задана калорийность сi одной весовой единицы i-го продукта (i принадлежит {1, 2, ..., n}). Требуется определить оптимальный состав рациона продуктов, такой, чтобы каждое питательное вещество содержалось в нем в необходимом количестве, обеспечивающем суточную потребность человека, и при этом суммарная калорийность рациона была минимальной.
Для решения задачи об оптимальной диете с помощью программы MS Excel необходимо задать конкретные значения параметрам исходной задачи. Для определенности предположим, что в качестве исходных типов продуктов рассматриваются: хлеб, мясо, сыр, бананы, огурцы, помидоры, виноград (n = 7), а в качестве питательных веществ рассматриваются белки, жиры, углеводы (m = 3). Калорийность одной весовой единицы каждого из продуктов следующая:с1 = 2060,с2= 2430,с3= 3600,с4= 890,с5= 140,с6= 230, с7 = 650. Содержание питательных веществ в каждом из продуктов может быть задано в форме следующей таблицы (см. табл.).
| Продукты/питательные вещества | Хлеб ржаной | Мясо баранина | Сыр "Российский" | Банан | Огурцы | Помидоры | Виноград |
|---|---|---|---|---|---|---|---|
| Белки | 66 | 225 | 235 | 20 | 13 | 16 | 11 |
| Жиры | 17 | 177 | 295 | 1 | 1 | 7 | 7 |
| Углеводы | 425 | 0 | 0 | 217 | 31 | 43 | 200 |
Минимальная суточная потребность в питательных веществах следующая: в белках b 1 = 105, в жирах b 2 = 75, в углеводах b 3 = 405.
Определить суточную потребности в питательных веществах (белки, жиры, углеводы) и общую калорийность оптимальной диеты.
Вариант 11.
Предприятие электронной промышленности выпускает две модели радиоприемников, причем каждая модель производится на отдельной технологической линии. Суточный объем производства первой линии – 60 изделий, второй линии – 75 изделий. На радиоприемник первой модели расходуются 10 однотипных элементов электронных схем, на радиоприемник второй модели – 8 таких же элементов. Максимальный суточный запас используемых элементов равен 800 единицам. Прибыль от реализации одного радиоприемника первой и второй моделей равна $30 и $20 соответственно. Определить оптимальный суточный объем производства первой и второй моделей.
Вариант 12.
Процесс изготовления двух видов промышленных изделий состоит в последовательной обработке каждого из них на трех станках. Время использования этих станков для производства данных изделий ограничено 10 ч. в сутки. Найти оптимальный объем производства изделий каждого вида.

Вариант 13.
Фирма имеет возможность рекламировать свою продукции, используя местные радио- и телевизионную сеть. Затраты на рекламу в бюджете фирмы ограничены $1000 в месяц. Каждая минута радиорекламы обходится в $5, а минута телерекламы – в $100. Фирма хотела бы использовать радиосеть, по крайней мере, в два раза чаще, чем сеть телевидения. Опыт прошлых лет показал, что объем сбыта, который обеспечивает каждая минута телерекламы, в 25 раз больше сбыта, обеспечиваемого одной минутой радиорекламы. Определить оптимальное распределение ежемесячно отпускаемых средств между радио- и телерекламой.
Вариант 14.
Фирма производит два вида продукции – A и B. Объем сбыта продукции вида A составляет не менее 60% общего объема реализации продукции обоих видов. Для изготовления продукции А и В используется одно и то же сырье, суточный запас которого ограничен величиной 100 кг. Расход сырья на единицу продукции A составляет 2 кг, а на единицу продукции В – 4 кг. Цены продукции А и В равны $20 и $40 соответственно. Определить оптимальное распределение сырья для изготовления продукции А и В.
Вариант 15.
Фирма выпускает ковбойские шляпы двух фасонов. Трудоемкость изготовления шляпы фасона 1 вдвое выше трудоемкости изготовления шляпы фасона 2. Если бы фирма выпускала только шляпы фасона 1, суточный объем производства мог бы составить 60 шляп. Суточный объем сбыта шляп обоих фасонов ограничен диапазоном от 50 до 100 штук. Прибыль от продажи шляпы фасона 1 равна $8, а фасона 2 – $5. Определить какое количество шляп каждого фасона следует изготавливать, чтобы максимизировать прибыль.
Вариант 16.
Изделия четырех типов проходят последовательную обработку на двух станках. Время обработки одного изделия каждого типа на каждом из станков:

Затраты на производство одного изделия каждого типа определяются как величины, прямо пропорциональные времени использования станков (в машино-часах). Стоимость машино-часа составляет $10 и $15 для станка 1 и 2 соответственно. Допустимое время для использования станков для обработки изделий всех типов ограничено следующими значениями: 500 машино-часов – для станка 1 и 380 машино-часов для станка 2. Цены изделий типов 1,2,3 и 4 равны $65, $70, $55 и $45 соответственно. Составить план производства максимизирующий чистую прибыль.
Вариант 17.
Завод выпускает изделия трех моделей (I, II III). Для их изготовления используется два вида ресурсов (А и В), запасы которых составляют – 4000 и 6000 единиц. Расходы ресурсов на одно изделие каждой модели:

Трудоемкость изготовления модели I вдвое больше, чем изделия модели II, и втрое больше, чем изделие модели III. Численность рабочих завода позволяет выпускать 1500 изделий I. Анализ условий сбыта показывает, что минимальный спрос на продукцию завода составляет 200, 200 и 150 изделий моделей I,II и III соответственно. Однако соотношение выпуска изделий моделей I,II и III должно быть равно 3:2:5. Удельная прибыль от реализации изделий моделей I,II и III составляет $30, $20 и $50 соответственно. Определить выпуск изделий, максимизирующий прибыль.
Вариант 18.
Некоторое производственное предприятие выпускает три вида клея. Для производства клея используется 4 типа химических веществ: крахмал, желатин, квасцы и мел. Расход этих веществ в кг для получения 1 кг каждого вида клея и их запас на складе предприятия представлены в таблице.
| Вид клея /Химические вещества | Клей № 1 | Клей № 2 | Клей № 3 | Запас на складе |
|---|---|---|---|---|
| Крахмал | 0,4 | 0,3 | 0,2 | 20 |
| Желатин | 0,2 | 0,3 | 0,4 | 35 |
| Квасцы | 0,05 | 0,07 | 0,1 | 7 |
| Мел | 0,01 | 0,05 | 0,15 | 10 |
Стоимость каждого вида клея для оптовых покупателей следующая:с1 = 380 руб/кг,с2 =430 руб/кг,с3 = 460 руб/кг. Требуется определить оптимальный объем выпуска клея каждого вида, обеспечивающий максимум общей стоимости готовой продукции.
Вариант 19.
Бройлерное хозяйство птицеводческой фермы насчитывает 20000 цыплят, которые выращиваются до 8-недельного возраста и после соответствующей обработки поступают в продажу. Хотя недельный рацион цыплят зависит от их возраста, в дальнейшем будем считать, что в среднем (за 8 недель) он составляет 1 фунт.
Для того чтобы цыплята достигли к восьмой неделе необходимых весовых кондиций, кормовой рацион должен удовлетворять определенным требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов или ингредиентов. Ограничим наше рассмотрение только тремя ингредиентами: известняком, зерном и соевыми бобами. Ниже приведены данные, характеризующие содержание (по весу) питательных веществ в каждом из ингредиентов и удельную стоимость каждого ингредиента.
Смесь должна содержать:
- не менее 0.8%, но не более 1.2% кальция;
- не менее 22% белка;
- не более 5% клетчатки.
Необходимо определить количество каждого из трех ингредиентов, образующих смесь минимальной стоимости при соблюдении требований к общему расходу кормовой смеси и ее питательности.
Вариант 20.
Имеется конечное число видов продуктов питания: ананас, арбуз, грейпфрут, язык говяжий, сардельки говяжьи, хлеб "Бородинский", картофель (n = 7), а в качестве питательных веществ рассматриваются белки, жиры, углеводы (m = 3). Калорийность 1 кг каждого из продуктов следующая:с1 = 470,с2= 380,с3 = 350,с4 = 1460,с5 = 2150,с6 = 2070, с7 = 800. Минимальная суточная потребность в питательных веществах следующая: в белках b 1 = 100, в жирах b 2 = 70, в углеводах b3 = 400. Содержание питательных веществ в каждом из продуктов может быть задано в форме нижеприведенной таблицы (табл.).
Требуется определить такой рацион питания, чтобы каждое питательное вещество содержалось в нем в необходимом количестве, обеспечивающем суточную потребность человека, и при этом суммарная калорийность рациона была минимальной.
| Продукты/Питательные вещества | Ананас | Арбуз | Грейпфрут | Язык говяжий | Сардельки говяжьи | Хлеб "Бородинский" | Картофель |
|---|---|---|---|---|---|---|---|
| Белки | 4 | 7 | 9 | 122 | 114 | 68 | 20 |
| Жиры | 2 | 2 | 2 | 109 | 182 | 13 | 4 |
| Углеводы | 115 | 88 | 65 | 0 | 15 | 407 | 163 |
КОНТРОЛЬНЫЕ ВОПРОСЫ
- Сформулировать основную задачу линейного программирования. Записать математическую модель ЗЛП.
- Для чего предназначена надстройка Поиск решения?
- Что понимают под целевой ячейкой, изменяемыми ячейками?
- Основные этапы решения ЗЛП с помощью процессора Excel.
- Как сохранить установочные параметры для поиска решения в виде модели?
- Какие существуют виды отчетов и как их создать? Продемонстрировать на примере.