|
Могу ли я получить сертификат о повышении квалификации если записывался на курс, не как на повышение квалификации. Курс пройден. И сколько действуют результаты курса? |
Формулы Шеннона и типы линий передачи, в которых используются модемы
В первоначальном смысле модем (модулятор-демодулятор) – это устройство, преобразующее цифровые данные от компьютера в аналоговые сигналы перед их передачей по последовательной линии и, после передачи, производящее обратное преобразование. Основная цель преобразования состоит в согласовании полосы частот, занимаемой сигналами, с полосой пропускания линии передачи. Сигналы могут занимать всю полосу пропускания линии передачи либо ее часть (при частотном разделении каналов, например, в случае организации полностью дуплексного обмена). Кроме того, модемы должны обеспечивать необходимую амплитуду и мощность сигналов для достижения большого отношения сигнал/шум и, как следствие обоих перечисленных факторов (полосы частот и отношения сигнал/шум), возможно большей скорости передачи. Подчеркивание основной (но не единственной) выполняемой модемами функции в названии устройств данного типа исторически связано с наиболее распространенным вариантом подключения отдельных компьютеров либо локальных сетей к аналоговой телефонной линии и, через нее, к другим компьютерам и сетям, в том числе к глобальной сети Интернет. Возможно, однако, использование достаточно экзотичных ( по крайней мере, в настоящее время) линий передачи (силовая линия электропитания или система кабельного телевидения) и не менее экзотичных модемов для связи компьютеров (и других устройств), подключенных к той же линии. Развиваются цифровые телефонные сети и сети передачи данных, в которых функции модемов изменяются (в частности, модуляция/демодуляция заменяется кодированием), но базовое название, тем не менее, сохраняется.
Еще 5 лет назад трудно было предсказать, что станут практически доступными решения, обеспечивающие бурный рост скорости передачи информации по обычной аналоговой телефонной линии (более чем в 200 раз для технологии ADSL в сравнении со стандартом V.34). И это в условиях, когда, казалось бы, все резервы увеличения скорости были исчерпаны и достигнут теоретический предел скорости, определяемый теоремами Шеннона! Без сомнения, методы и средства обмена информацией между локальными сетями (или отдельными компьютерами) и глобальными сетями будут совершенствоваться и далее. Обзор доступных и перспективных технологий в этой области, представленный в данной главе, имеет целью не только их сравнительный анализ по характеристикам (прежде всего, по скорости передачи информации и расстоянию), но и пояснение принципов функционирования различных линий передачи, в которых используются модемы, и обеспечивается достижение предельных характеристик.
Формулы Шеннона для непрерывного и дискретного каналов
Формулы Шеннона представляют собой математические записи теорем кодирования Шеннона для дискретных и непрерывных сообщений, передаваемых по каналам с ограниченной пропускной способностью на фоне шумов и помех. Каналы в зависимости от типов сигналов на входе и выходе принято делить на дискретные, непрерывные и смешанные. В общей структурной схеме канала передачи (см. рис. 17.1) дискретными являются каналы от входа модулятора до выхода демодулятора и от входа кодера до выхода декодера. Непрерывный (аналоговый) канал – это собственно последовательная линия передачи (телефонная линия, скрученная пара проводов, коаксиальный кабель и др.). Дискретные каналы не являются независимыми от аналогового канала, который часто образует наиболее "узкое место" при передаче и из-за собственной ограниченной полосы пропускания, внешних шумов и помех определяет общую достижимую скорость передачи (при заданном допустимом уровне ошибок при приеме).

Рис. 17.1. Общая структурная схема канала передачи: 1 – непрерывный (аналоговый) канал; 2, 3 – дискретные каналы
Прежде, чем рассматривать формулы Шеннона, целесообразно обратиться к рис. 17.1 и пояснить функции отдельных устройств. Кодер/декодер в конкретной системе может совмещать, на первый взгляд, прямо противоположные функции. Во-первых, кодер может быть использован для внесения избыточности в передаваемую информацию с целью обнаружения влияния шумов и помех на приемном конце (там этим занимается соответствующий декодер). Избыточность проявляется в добавлении к передаваемой полезной информации так называемых проверочных разрядов, формируемых, как правило, аппаратными средствами из информационной части сообщения. Известно много различных помехоустойчивых кодов, причем самый простой из них однобитовый (бит четности/нечетности) далеко не всегда удовлетворительно работает на практике. Вместо него в локальных сетях используются контрольная сумма или циклический код (CRC – Cyclic Redundancy Check), занимающий в формате передаваемого сообщения 2 или 4 байта, независимо от длины в байтах информационной части сообщения. При больших объемах передаваемой информации целесообразно сжать ее до передачи. В этом случае говорят уже о статистическом кодировании. Здесь уместна аналогия с обычными программами архивации файлов (типа arj, rar, pkzip и др.), которые широко используются при организации обмена в Интернет. Если проблема с большими объемами информации и после такого обратимого сжатия до конца не решается, можно рассмотреть возможность необратимого сжатия информации с частичной ее потерей ("огрублением"). Конечно, здесь не идет речь об отбрасывании части цифровых данных, но по отношению к изображениям иногда можно пойти на снижение разрешения (числа пикселей) без искажения общего вида "картинки". Понятно, что оба типа кодирования (помехоустойчивое избыточное кодирование и статистическое кодирование) служат, в конечном счете, решению одной задачи – повышению качества передачи как в смысле отсутствия или минимального допустимого уровня ошибок в принятом сообщении, так и в смысле максимального использования пропускной способности канала передачи. В высокоскоростных модемах нередко реализуются оба типа кодирования. Что касается функций модулятора/демодулятора на рис. 17.1, то они, как уже было сказано, включают согласование полосы частот, занимаемой сигналами, с полосой пропускания линии передачи. Кроме того, выходные каскады передатчиков (после модуляторов) реализуют усиление сигналов по мощности и амплитуде, это одно из средств увеличения отношения сигнал/шум. Действительно, ничто (кроме, пожалуй, техники безопасности) не заставляет разработчиков придерживаться в аналоговом канале столь жестких ограничений сигналов по амплитуде, как в дискретных (цифровых) каналах (от 0 до +5В при использовании аппаратуры в стандарте ТТЛ). Например, для распространенного стандарта последовательного порта компьютера RS-232C предусмотрена "вилка" амплитуд от –(3...12) В до +(3...12) В. Конечно, это касается амплитуд вблизи передатчика, в то время как вблизи приемника амплитуда сигналов может быть существенно ослаблена.
Формула Шеннона для непрерывного (аналогового) канала достаточна проста:
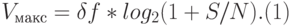
где Vмакс – максимальная скорость передачи (бит/сек), 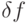 – полоса пропускания линии передачи и, одновременно, полоса частот, занимаемая сигналами (если не используется частотное разделение каналов), S/N – отношение сигнал/шум по мощности. График этой зависимости приведен на
рис.
17.2(формуле Шеннона соответствует кривая под названием " теоретический предел ").
– полоса пропускания линии передачи и, одновременно, полоса частот, занимаемая сигналами (если не используется частотное разделение каналов), S/N – отношение сигнал/шум по мощности. График этой зависимости приведен на
рис.
17.2(формуле Шеннона соответствует кривая под названием " теоретический предел ").

Рис. 17.2. Зависимость максимальной скорости передачи Vмакс для аналоговой линии от отношения сигнал-шум по мощности S/N
Под шумом понимается любой нежелательный сигнал, в том числе внешние помехи или сигнал, вернувшийся к передающему устройству – может быть и модему – в результате отражения от противоположного конца линии. Сами по себе сосредоточенные помехи не столь существенно ограничивают пропускную способность аналогового канала, как непредсказуемый в каждый момент времени белый гауссовский шум. "Умные" высокоскоростные модемы умеют, как будет отмечено в дальнейшем, определять уровень и задержку "своих" отраженных сигналов и компенсировать их влияние.
Формула Шеннона для многопозиционного дискретного канала, построенного на базе предыдущего непрерывного канала, в отсутствие ошибок при приеме, имеет следующий вид:
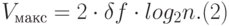
Здесь n – общее число вариантов дискретного (цифрового) сигнала (алфавит). Если за время одной посылки (длительность элементарного аналогового сигнала типа отрезка синусоиды) передается информация о k двоичных разрядах, то n=2k. Практически расширение алфавита для дискретных сигналов приводит к появлению все менее различимых элементарных посылок, так что величина n ограничивается сверху все тем же отношением сигнал/шум S/N в аналоговом канале.
При учете ошибок при приеме формула Шеннона для многопозиционного дискретного канала, построенного на базе непрерывного канала, имеет следующий вид:
![V_{макс}=2 \cdot \delta f \cdot [log_{2}n + p_{ош} \cdot log_{2}(p_{ош}/(n – 1)) + (1 – p_{ош}) \cdot log_{2}(1 – p_{ош})]. (3)](/sites/default/files/tex_cache/c71b2721518b5d02905e1c8fd1a4450a.png)
Здесь pош – отношение числа бит, принятых с ошибками, к общему числу переданных бит за время наблюдения, теоретически стремящееся к бесконечности, а практически достаточное для набора статистики. Согласно стандарта ITU-T для телефонных сообщений должно выполняться условие pош<=3*10-5, а для цифровых данных pош<=10-6 (в отдельных случаях для критичных данных этот порог уменьшают до 10-9 ). При выполнении требований стандартов влиянием ошибок при приеме на максимально-допустимую скорость передачи можно полностью пренебречь и от соотношения (3) перейти к более простому соотношению (2). В частном случае бинарного канала ( k=1, n=2 ) при pош=1/2 из соотношения (3) следует, что Vмакс=0, а при pош->0 и при pош->1  . Физический смысл такой зависимости состоит в том, что при pош=1/2 принятый сигнал не содержит полезной информации (каждый из принятых битов может оказаться ошибочным). При pош->1 (гипотетический случай, имеющий сугубо теоретический интерес) каждый бит с большой вероятностью инвертируется и доля полезной информации снова возрастает.
. Физический смысл такой зависимости состоит в том, что при pош=1/2 принятый сигнал не содержит полезной информации (каждый из принятых битов может оказаться ошибочным). При pош->1 (гипотетический случай, имеющий сугубо теоретический интерес) каждый бит с большой вероятностью инвертируется и доля полезной информации снова возрастает.
Формулы Шеннона показывают, что наиболее эффективный способ повышения максимальной скорости передачи Vмакс состоит в увеличении полосы пропускания линии передачи  . Логарифмическая зависимость Vмакс от отношения сигнал/шум S/N делает этот путь повышения Vмакс гораздо менее перспективным и более трудоемким. Однако на практике редко возможен свободный выбор линии передачи, который с точки зрения реализации максимальной скорости передачи однозначно сводится к использованию оптоволокна (ВОЛС). На практике чаще всего имеется телефонная линия, по которой и нужно организовать передачу с применением модемов. Аналоговая телефонная линия (точнее, тракт передачи, функционирующий на этой линии, с учетом фильтров) имеет фиксированную полосу пропускания
. Логарифмическая зависимость Vмакс от отношения сигнал/шум S/N делает этот путь повышения Vмакс гораздо менее перспективным и более трудоемким. Однако на практике редко возможен свободный выбор линии передачи, который с точки зрения реализации максимальной скорости передачи однозначно сводится к использованию оптоволокна (ВОЛС). На практике чаще всего имеется телефонная линия, по которой и нужно организовать передачу с применением модемов. Аналоговая телефонная линия (точнее, тракт передачи, функционирующий на этой линии, с учетом фильтров) имеет фиксированную полосу пропускания 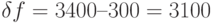 Гц, поэтому приходится бороться именно за повышение отношения сигнал/шум. Да и то хороший результат сам по себе не гарантирован, так как речь идет о реализации возможностей, близких к теоретическому пределу. Практический предел отношения сигнал/ шум в аналоговой телефонной линии составляет примерно 35 дБ (более 3000 раз по мощности или более 56 раз по амплитуде), что соответствует максимальной скорости
Гц, поэтому приходится бороться именно за повышение отношения сигнал/шум. Да и то хороший результат сам по себе не гарантирован, так как речь идет о реализации возможностей, близких к теоретическому пределу. Практический предел отношения сигнал/ шум в аналоговой телефонной линии составляет примерно 35 дБ (более 3000 раз по мощности или более 56 раз по амплитуде), что соответствует максимальной скорости 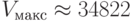 бит/сек (стандартное значение, реализуемое на практике, 33600 бит/сек). Популярные в настоящее время 56К – модемы реализуют заявленную скорость только в одну сторону – от провайдера (из сети) до пользователя и только при условии работы провайдера непосредственно на цифровой, несколько более широкополосной, линии передачи (чудес не бывает!).
бит/сек (стандартное значение, реализуемое на практике, 33600 бит/сек). Популярные в настоящее время 56К – модемы реализуют заявленную скорость только в одну сторону – от провайдера (из сети) до пользователя и только при условии работы провайдера непосредственно на цифровой, несколько более широкополосной, линии передачи (чудес не бывает!).
