|
Добрый день! Подскажите пжл, не разобралась, обучение все платное? Мне сказали бесплатное есть... |
Олигополия
9.2. Поведение фирмы в краткосрочном и долгосрочном периодах
Субъективный фактор - политика конкурентов
При определении рыночного поведения олигополиста огромную роль играет субъективный фактор - характер взаимоотношений между конкурирующими на рынке фирмами. В этом состоит уникальная особенность олигополии. При всех других типах рынков значение субъективной политики фирм-конкурентов невелико. В условиях совершенной и отчасти монополистической конкуренции на рынке действует такое множество фирм, что особенности поведения каждой из фирм-конкурентов не поддаются учету. А при монополии конкурентов вообще нет. И только на олигополистическом рынке решение каждого из немногочисленного круга фирм-олигополистов непосредственно сказывается на всех остальных его участниках и на отрасли в целом.
Дуополия
Лучше понять закономерности поведения фирмы на олигополистическом рынке позволяет анализ дуополии, т.е. простейшей олигополистической ситуации, когда на рынке действуют только две конкурирующие между собой фирмы. Главная особенность моделей дуополий состоит в том, что выручка и, следовательно, прибыль, которую получит фирма, зависит не только от ее решений, но и от решений фирмы-конкурента, также заинтересованной в максимизации своей прибыли. Процесс принятия решения на олигополистическом рынке напоминает анализ отложенной шахматной партии, где игрок ищет самые сильные ответы на возможные варианты хода своего противника.
Модель Курно
Существует много моделей олигополии, и ни одну из них нельзя считать универсальной, тем не менее общую логику поведения фирм на этом рынке они объясняют. Первая модель дуополии была предложена французским экономистом Огюстеном Курно еще в 1838 г.
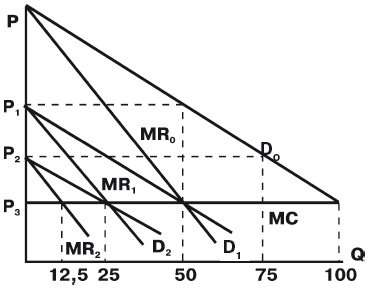
Модель Курно анализирует поведение фирмы-дуополиста исходя из допущения, что ей известен объем выпуска продукции, который ее единственный конкурент уже выбрал для себя. Задача фирмы состоит в том, чтобы определить собственный размер производства, сообразуясь с решением конкурента как с данностью. На рис. 9.2 показано, каким было бы поведение фирмы в таких условиях.
Краткосрочный период
Чтобы не усложнять график, мы сделали два дополнительных упрощения. Во-первых приняли, что оба дуополиста - совершенно одинаковые, ничем не отличающиеся компании. Во-вторых, допустили, что предельные издержки обеих фирм постоянны: кривая MC идет строго горизонтально.
Допустим вначале, что фирме № 1 твердо известно, что конкурент не собирается вообще ничего выпускать. В этом случае фирма № 1 фактически является монополией. Кривая спроса на ее продукцию (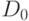 ) поэтому совпадет с кривой спроса всей отрасли. Соответственно кривая предельного дохода займет некоторое положение (
) поэтому совпадет с кривой спроса всей отрасли. Соответственно кривая предельного дохода займет некоторое положение ( ). Пользуясь обычным правилом равенства предельного дохода и предельных издержек MC = MR, фирма № 1 установит оптимальный для себя объем производства (в изображенном на графике случае - 50 ед.).
). Пользуясь обычным правилом равенства предельного дохода и предельных издержек MC = MR, фирма № 1 установит оптимальный для себя объем производства (в изображенном на графике случае - 50 ед.).
А если фирме № 1 станет известно, что ее конкурент сам намерен выпустить 50 ед. продукции? На первый взгляд может показаться, что тем самым он исчерпает весь объем спроса и вынудит фирму № 1 отказаться от производства. Однако это не так. Если фирма № 1 установит на свою продукцию цену  , то спроса на нее действительно не будет: те 50 ед., которые рынок готов принять по этой цене, уже поставлены фирмой № 2. Но если фирма № 1 установит цену
, то спроса на нее действительно не будет: те 50 ед., которые рынок готов принять по этой цене, уже поставлены фирмой № 2. Но если фирма № 1 установит цену 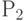 , то общий спрос рынка составит 75 ед. (см. кривую спроса отрасли
, то общий спрос рынка составит 75 ед. (см. кривую спроса отрасли 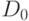 ). Поскольку фирма № 2 предлагает только 50 ед., то на долю фирмы № 1 останется 25 ед. (75–50 = 25). Если же цена будет опущена до
). Поскольку фирма № 2 предлагает только 50 ед., то на долю фирмы № 1 останется 25 ед. (75–50 = 25). Если же цена будет опущена до 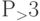 , то, повторив аналогичные рассуждения, можно установить, что потребность рынка в продукции фирмы № 1 составит 50 ед. (100–50 = 50).
, то, повторив аналогичные рассуждения, можно установить, что потребность рынка в продукции фирмы № 1 составит 50 ед. (100–50 = 50).
Легко понять, что перебирая разные возможные уровни цен, мы будем получать и разные уровни потребности рынка в продукции фирмы № 1. Иными словами, на продукцию фирмы № 1 сформируется новая кривая спроса (на нашем графике - 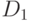 ) и соответственно новая кривая предельного дохода (
) и соответственно новая кривая предельного дохода (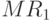 ). Снова использовав правило MC = MR, можно определить новый оптимальный объем производства (в нашем случае он составит 25 ед.).
). Снова использовав правило MC = MR, можно определить новый оптимальный объем производства (в нашем случае он составит 25 ед.).
Объем производства в условиях олигополии
Уже на этом этапе анализа модель Курно позволяет сделать важные экономические выводы. При олигополии объем производства больше того уровня, который установился бы при чистой монополии, но меньше, чем сложился бы при совершенной конкуренции.

Действительно, две наши фирмы в сумме выпускают 75 ед., тогда как монополия выпустила бы только 50 ед. А при совершенной конкуренции выпуск составил бы 100 ед. Напомним, что при совершенной конкуренции кривые спроса и предельного дохода совпадают (D = MR), следовательно, точка равновесия по правилу MC = MR должна установиться на пересечении кривых D и МС.
Цены в условиях олигополии
В свою очередь цены при олигополии ниже монополистических, однако превышают конкурентные:

На графике хорошо видно, что цена, которую установит фирма № 1 и которую вынуждена будет поддержать и фирма № 2, если она хочет продать свои 50 ед. продукции, установится на уровне 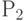 . Ведь только при этом уровне цен рынок сможет поглотить все 75 ед., выпущенные обеими фирмами. А цена
. Ведь только при этом уровне цен рынок сможет поглотить все 75 ед., выпущенные обеими фирмами. А цена 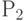 ниже монопольной цены
ниже монопольной цены  и выше конкурентного уровня
и выше конкурентного уровня  .
.
Ясен и экономический механизм, приводящий к установлению описанного уровня цен и производства. Ограничивая производство и завышая, цены монополия оставляет неудовлетворенной часть рыночного спроса. Этот остаток и служит рынком сбыта для второго дуополиста (а также третьего, четвертого и т.д. конкурентов, если мы перейдем от дуополистической модели к многофирменной олигополии), позволяя ему выпустить дополнительную продукцию, если, конечно, его цены будут ниже монопольного уровня.
Олигополистические прибыли
Прямым следствием описанной ситуации является также вывод о том, что суммарные олигополистические прибыли обоих дуополистов окажутся ниже тех прибылей, которые на том же рынке получила бы единственная фирма-монополист, хотя тенденция к получению положительных экономических прибылей сохранится.
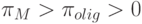
Последний тезис - наличие экономических прибылей - доказательства, собственно, не требует: так обстоит дело на любом рынке несовершенной конкуренции. Меньший же по сравнению с монополией их уровень легче всего это доказать от обратного. Как известно, правило MC = MR обеспечивает максимизацию прибылей. В самом начале анализа модели Курно мы убедились, что, если на рынке действует только одна фирма-монополист (ситуация, в которой про второго дуополиста известно, что он не планирует выпуска продукции, фактически равносильна монополии), она, руководствуясь этим правилом, установила бы некоторый объем производства и уровень цен (в нашем примере 50 ед. продукции и  ). При любом ином объеме выпуска (и уровне цен) прибыль будет меньше. Но ведь вмешательство второго дуополиста, начало выпуска продукции этой второй фирмой как раз и ведут к отклонению объемов производства и цен от оптимума.
Следовательно, и прибыль в дуополистической ситуации не будет столь велика, как при чистой монополии.
). При любом ином объеме выпуска (и уровне цен) прибыль будет меньше. Но ведь вмешательство второго дуополиста, начало выпуска продукции этой второй фирмой как раз и ведут к отклонению объемов производства и цен от оптимума.
Следовательно, и прибыль в дуополистической ситуации не будет столь велика, как при чистой монополии.
Зависимость кривой спроса от поведения конкурентов
Но вернемся к
рис.
9.2. Очевидно, что рассуждения, которые мы провели применительно к выпуску второй фирмой 0 ед. и 50 ед. продукции, можно повторить применительно к самым разным уровням производства этой фирмы. На
рис.
9.2, в частности, показана кривая спроса на продукцию фирмы № 1 (см.  ), которая возникнет при выпуске фирмой № 2 ровно 75 ед. продукции. В этом случае оптимальный объем производства для самой фирмы № 1 составит 12,5 ед. (пересечение
), которая возникнет при выпуске фирмой № 2 ровно 75 ед. продукции. В этом случае оптимальный объем производства для самой фирмы № 1 составит 12,5 ед. (пересечение 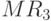 и MC).
и MC).
Очевиден и общий вывод из анализа краткосрочного равновесия в модели Курно: каждому уровню выпуска одного из дуополистов соответствует особая кривая спроса на продукцию второго дуополиста. Иными словами, для любого олигополиста объем рынка не является постоянной величиной, а прямо зависит от решений конкурентов.
Равновесие Курно
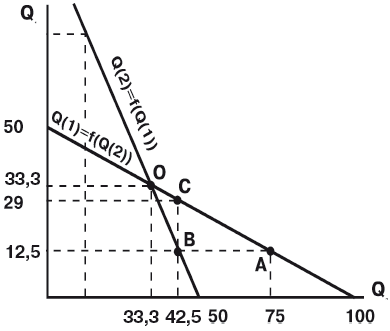
Чтобы лучше уяснить все последствия этой закономерности, обратимся к рис. 9.3.
Размеры выпуска продукции фирмой № 1 изображены как кривая реакции на объем производства фирмы № 2. Аналогичным образом выпуск продукции фирмой № 2 представлен как функция от объема производства фирмы № 1:

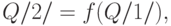
где Q/1/ - объем производства фирмы № 1, а Q/2/ - объем производства фирмы № 2.
Посмотрим, смогут ли обе фирмы установить взаимоприемлемые объемы производства? Все данные для графика мы взяли из предыдущего примера. Так, если о фирме № 2 известно, что она собирается выпустить 75 ед. продукции, то фирма № 1 примет решение о выпуске 12,5 ед. (см. точку А). Но если фирма № 1 действительно выпустит 12,5 ед., то, как видно на графике, фирма № 2 в соответствии со своей кривой реакции должна выпустить не 75, а 42,5 ед. (точка В). Но такой уровень выпуска продукции конкурентом вынудит фирму № 1 выпустить не 12,5 ед., как она собиралась, а 29 ед. (точка С) и т.д.
Легко заметить, что уровень производства, устанавливаемый компанией исходя из сложившегося размера производства конкурента, каждый раз оказывается таким, что заставляет последнего пересмотреть его. Это вызывает новую корректировку объема производства первой фирмы, что в свою очередь снова изменяет планы второй, т.е. ситуация является неустойчивой, неравновесной.
Однако существует и точка устойчивого равновесия - это точка пересечения кривых реакции обеих фирм (на графике - точка О). В нашем примере, фирма № 1 выпускает 33,3 ед., исходя из того, что конкурент выпустит столько же. А для последнего выпуск 33,3 ед. действительно является оптимальным. Каждая из фирм выпускает объем продукции, максимизирующий ее прибыли при данном объеме производства конкурента. Ни одной из фирм не выгодно менять объем производства, следовательно, равновесие устойчиво. Оно получило в теории название равновесия Курно.
Под равновесием Курно понимается такое сочетание объемов выпуска каждой из фирм, при котором ни у одной из них нет стимулов для изменения своего решения: прибыль каждой фирмы максимальна при условии, что конкурент сохранит данный объем выпуска. Или по-другому: в точке равновесия Курно ожидаемый конкурентами объем выпуска продукции любой из фирм совпадает с фактическим и при этом является оптимальным.
Математическая теория игр показывает, что равновесие Курно при одних допущениях о логике поведения дуополистов достигается, а при других - нет. При этом решающее значение для достижения равновесия является понятность (предсказуемость) действий партнера-конкурента и готовность его к кооперативному поведению с соперником.