| Россия |
Решение задач комбинаторной оптимизации рекуррентными сетями
Решение задачи коммивояжера сетью Хопфилда
Рассмотрим задачу коммивояжера для  городов. Известны
расстояния
городов. Известны
расстояния 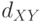 между каждой парой городов
между каждой парой городов  ; коммивояжер, выходя из одного
города,
должен посетить
; коммивояжер, выходя из одного
города,
должен посетить  других городов, заходя по одному разу в
каждый, и
вернуться в исходный. Требуется определить порядок обхода городов, при
котором общее пройденное расстояние минимально.
других городов, заходя по одному разу в
каждый, и
вернуться в исходный. Требуется определить порядок обхода городов, при
котором общее пройденное расстояние минимально.
Пусть сеть Хопфилда состоит из  нейронов, а состояние
нейронов
описывается двойными индексами
нейронов, а состояние
нейронов
описывается двойными индексами 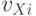 , где индекс
, где индекс  связан с именем города,
связан с именем города,  - с позицией города в маршруте коммивояжера. Запишем
функцию
вычислительной энергии для сети, предназначенной решать задачу
коммивояжера. В ней состояние с наименьшей энергией должно соответствовать
самому короткому маршруту. Функция энергии должна удовлетворять следующим
требованиям:
- с позицией города в маршруте коммивояжера. Запишем
функцию
вычислительной энергии для сети, предназначенной решать задачу
коммивояжера. В ней состояние с наименьшей энергией должно соответствовать
самому короткому маршруту. Функция энергии должна удовлетворять следующим
требованиям:
1) должна поддерживать устойчивое состояние в форме матрицы
 |
( 1) |
в которой строки соответствуют городам, столбцы - их номерам в маршруте; в каждой строке и каждом столбце только одна единица, остальные нули;
2) из всех решений вида (1) функция энергии должна поддерживать те, которые соответствуют коротким маршрутам.
Таким требованиям удовлетворяет функция энергии в виде:
 |
( 2) |
где первые три члена поддерживают первое требование, четвертый член —
второе. Первый член равен нулю, если каждая строка  содержит не
более
одной единицы. Второй равен нулю, если каждый столбец
содержит не
более
одной единицы. Второй равен нулю, если каждый столбец  содержит
не более
одной единицы. Третий равен нулю, если в матрице всего
содержит
не более
одной единицы. Третий равен нулю, если в матрице всего  единиц.
Короткие маршруты поддерживает четвертый член. В нем индексы
единиц.
Короткие маршруты поддерживает четвертый член. В нем индексы  берутся по
модулю
берутся по
модулю  для того, чтобы показать, что
для того, чтобы показать, что  -й город
соседствует в маршруте с
-й город
соседствует в маршруте с 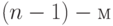 , т.е.
, т.е. 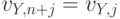 . Четвертый
член численно равен длине маршрута.
Каноническое выражение для функции вычислительной энергии имеет вид
. Четвертый
член численно равен длине маршрута.
Каноническое выражение для функции вычислительной энергии имеет вид
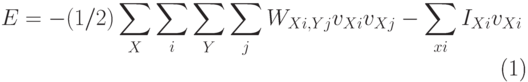 |
( 3) |
Из (2) и (3) получаем веса сети Хопфилда:
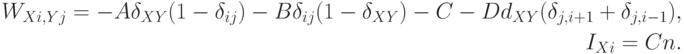
Здесь  - символ Кронекера.
- символ Кронекера.
Моделирование работы сети Хопфилда показало, что лучшее по качеству
решение дает сеть, нейроны которой имеют сигмовидную характеристику, а
сеть, в которой нейроны имеют ступенчатые переходы, приходила к финальным
состояниям, соответствующим маршрутам немного лучшим, чем случайные.
Многочисленные исследования показывают, что качество решения задачи
минимизации функции энергии (2) существенно зависит от выбора
производной
сигмовидной униполярной функции активации нейрона в окрестности нуля. При
малой величине производной минимумы энергии оказываются в центре гиперкуба
решений (некорректное решение), при большой величине производной сеть
Хопфилда попадает в вершину гиперкуба, соответствующую локальному минимуму
функции энергии. Кроме того, на качество решения существенное влияние
оказывает выбор коэффициентов 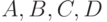 . Поиск методов
оптимального
выбора этих коэффициентов является в настоящее время предметом интенсивных
исследований.
. Поиск методов
оптимального
выбора этих коэффициентов является в настоящее время предметом интенсивных
исследований.
