| Россия |
Модели нейронов
Нейроны типа WTA
Нейроны типа WTA (Winner Takes All — "Победитель получает
все") имеют
входной модуль
в виде адаптивного сумматора. Выходной сигнал  -го сумматора
определяется по формуле
-го сумматора
определяется по формуле
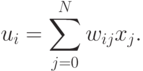
По результатам сравнения сигналов 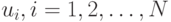 отдельных
нейронов победителем признается нейрон, у которого
отдельных
нейронов победителем признается нейрон, у которого  оказался
наибольшим.
Нейрон-победитель вырабатывает на своем выходе состояние 1, а
остальные
(проигравшие) нейроны переходят в состояние 0.
оказался
наибольшим.
Нейрон-победитель вырабатывает на своем выходе состояние 1, а
остальные
(проигравшие) нейроны переходят в состояние 0.
Для обучения нейронов WTA учитель не требуется. На начальном этапе
случайным образом
выбираются весовые коэффициенты 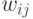 каждого нейрона,
нормализуемые относительно
1 по формуле
каждого нейрона,
нормализуемые относительно
1 по формуле

После подачи входного вектора  , компоненты которого
нормализованы по
формуле
, компоненты которого
нормализованы по
формуле
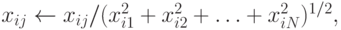
определяется победитель этапа. Победитель переходит в состояние
1, что
позволяет произвести уточнение весов его входных линий 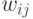 по
правилу
по
правилу
![w_{ij}(t+1) = w_{ij}(t)+ \alpha [x - w_{ij}(t)].](/sites/default/files/tex_cache/add6594e9c3576af0921dce3e89728a1.png)
Проигравшие нейроны формируют на своих выходах состояние 0, что блокирует процесс уточнения их весовых коэффициентов.
Выходной сигнал  -го нейрона может быть описан векторным
отношением
-го нейрона может быть описан векторным
отношением
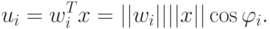
Поскольку 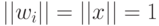 , значение
, значение  определяется углом между
векторами
определяется углом между
векторами  и
и 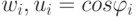 . Поэтому
победителем оказывается
нейрон, вектор весов которого оказывается наиболее близким текущему
обучающему вектору
. Поэтому
победителем оказывается
нейрон, вектор весов которого оказывается наиболее близким текущему
обучающему вектору  . В результате победы нейрона уточняются его
весовые
коэффициенты, значения которых приближаются к значениям текущего
обучающего вектора
. В результате победы нейрона уточняются его
весовые
коэффициенты, значения которых приближаются к значениям текущего
обучающего вектора  .
.
Следствием конкуренции нейронов становится самоорганизация процесса обучения. Нейроны уточняют свои веса таким образом, что при предъявлении группы близких по значениям входных векторов победителем всегда оказывается один и тот же нейрон. Системы такого типа чаще всего применяются для классификации векторов.
Кубические модели нейронов
Вектор  входных двоичных сигналов рассматривается как адрес
ячейки
памяти, содержимое которой равно 0 или 1. Для размерности
входных двоичных сигналов рассматривается как адрес
ячейки
памяти, содержимое которой равно 0 или 1. Для размерности  вектора
вектора  существует
существует 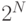 возможных адресов.
возможных адресов.
Можно рассматривать ячейки памяти, как вершины  -мерного
гиперкуба.
Ячейки памяти получают значения независимо друг от друга. Полезно
рассматривать ячейки памяти как содержащие поляризованные двоичные
значения
-мерного
гиперкуба.
Ячейки памяти получают значения независимо друг от друга. Полезно
рассматривать ячейки памяти как содержащие поляризованные двоичные
значения  . Тогда работа кубического модуля описывается
следующим
образом.
. Тогда работа кубического модуля описывается
следующим
образом.
Двоичный вход  используется как адрес памяти, поляризованная
двоичная
величина считывается и конвертируется в неполяризованную форму функцией
используется как адрес памяти, поляризованная
двоичная
величина считывается и конвертируется в неполяризованную форму функцией  (см. формулу 1). Обозначим значения по адресу
(см. формулу 1). Обозначим значения по адресу  через
через 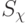 ,
так что
,
так что 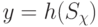 . Такие модули мы будем называть
кубическими, чтобы
подчеркнуть геометрическое представление множества адресов значений
активации как множество вершин гиперкуба.
. Такие модули мы будем называть
кубическими, чтобы
подчеркнуть геометрическое представление множества адресов значений
активации как множество вершин гиперкуба.
