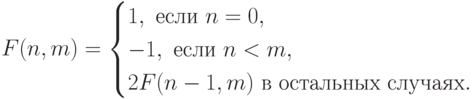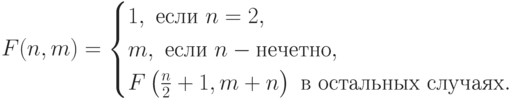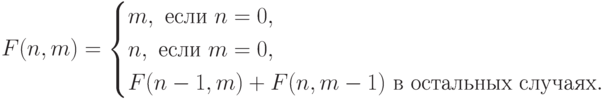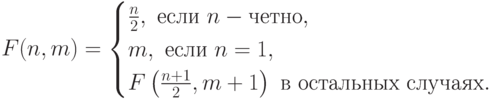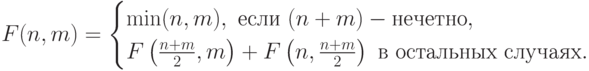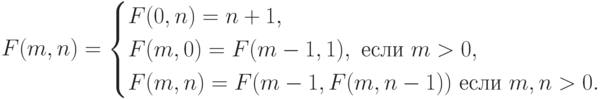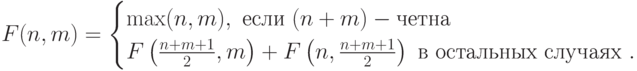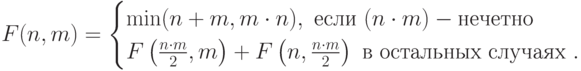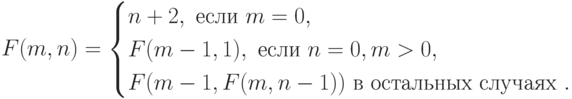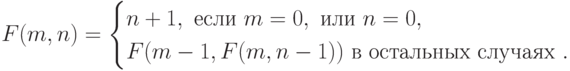Опубликован: 02.02.2011 | Уровень: для всех | Доступ: свободно
Лекция 48:
Задания
Задание 9. Рекурсивные алгоритмы
Разработайте рекурсивный алгоритм для решения задачи.
1-10. Определите закономерность формирования членов последовательности. Найдите  -ый член последовательности, сократив количество рекурсивных вызовов.
-ый член последовательности, сократив количество рекурсивных вызовов.
11-20. Найдите значение функции для любых целых неотрицательных аргументов.
21-28. Составьте рекурсивную функцию для решения задачи.
- Найдите сумму всех трехзначных чисел, кратных 25.
- Переведите натуральное число
 в восьмеричную систему счисления.
в восьмеричную систему счисления. - Найдите
 -ый член геометрической прогрессии, заданной первым членом и знаменателем.
-ый член геометрической прогрессии, заданной первым членом и знаменателем. - Найдите сумму первых
 четных натуральных чисел
четных натуральных чисел - Найдите
 -ый член арифметической прогрессии, заданной первым членом и разностью.
-ый член арифметической прогрессии, заданной первым членом и разностью. - Найдите сумму первых
 натуральных чисел, оканчивающихся цифрой 5.
натуральных чисел, оканчивающихся цифрой 5. - Функция определена на полуинтервале
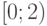 следующим образом:
следующим образом: 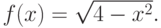 Выполните ее периодическое продолжение на множество действительных чисел. Найдите значение полученной функции для данного
Выполните ее периодическое продолжение на множество действительных чисел. Найдите значение полученной функции для данного  .
. - Переведите натуральное число
 в двоичную систему счисления.
в двоичную систему счисления.


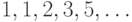
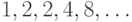
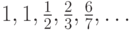
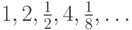
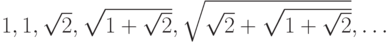
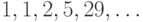
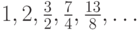
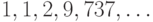
![1,2,\sqrt{2},\sqrt[4]{8},\sqrt[8]{32},\ldots](/sites/default/files/tex_cache/7ccb1e0c59e65a794c881fbebfeb370f.png)
![1,2,\frac{1}{\sqrt{2}},2\sqrt[4]{2},\frac{1}{\sqrt{4\sqrt[4]{2}}},\ldots](/sites/default/files/tex_cache/bb30454d58f1bf5a220586f0e95a9bff.png)