Алгоритмы поиска в линейных структурах
Цель лекции: изучить основные алгоритмы поиска в линейных структурах и научиться решать задачи поиска в линейных структурах на основе алгоритмов последовательного и бинарного поиска.
Одним из важнейших действий со структурированной информацией является поиск. Поиск – процесс нахождения конкретной информации в ранее созданном множестве данных. Обычно данные представляют собой записи, каждая из которых имеет хотя бы один ключ. Ключ поиска – это поле записи, по значению которого происходит поиск. Ключи используются для отличия одних записей от других. Целью поиска является нахождение всех записей (если они есть) с данным значением ключа.
Структуру данных, в которой проводится поиск, можно рассматривать как таблицу символов (таблицу имен или таблицу идентификаторов) – структуру, содержащую ключи и данные, и допускающую две операции – вставку нового элемента и возврат элемента с заданным ключом. Иногда таблицы символов называют словарями по аналогии с хорошо известной системой упорядочивания слов в алфавитном порядке: слово – ключ, его толкование – данные.
Поиск является одним из наиболее часто встречаемых действий в программировании. Существует множество различных алгоритмов поиска, которые принципиально зависят от способа организации данных. У каждого алгоритма поиска есть свои преимущества и недостатки. Поэтому важно выбрать тот алгоритм, который лучше всего подходит для решения конкретной задачи.
Поставим задачу поиска в линейных структурах. Пусть задано множество данных, которое описывается как массив, состоящий из некоторого количества элементов. Проверим, входит ли заданный ключ в данный массив. Если входит, то найдем номер этого элемента массива, то есть, определим первое вхождение заданного ключа (элемента) в исходном массиве.
Таким образом, определим общий алгоритм поиска данных:
Шаг 1. Вычисление элемента, что часто предполагает получение значения элемента, ключа элемента и т.д.
Шаг 2. Сравнение элемента с эталоном или сравнение двух элементов (в зависимости от постановки задачи).
Шаг 3. Перебор элементов множества, то есть прохождение по элементам массива.
Основные идеи различных алгоритмов поиска сосредоточены в методах перебора и стратегии поиска.
Рассмотрим основные алгоритмы поиска в линейных структурах более подробно.
Последовательный (линейный) поиск
Последовательный (линейный) поиск – это простейший вид поиска заданного элемента на некотором множестве, осуществляемый путем последовательного сравнения очередного рассматриваемого значения с искомым до тех пор, пока эти значения не совпадут.
Идея этого метода заключается в следующем. Множество элементов просматривается последовательно в некотором порядке, гарантирующем, что будут просмотрены все элементы множества (например, слева направо). Если в ходе просмотра множества будет найден искомый элемент, просмотр прекращается с положительным результатом; если же будет просмотрено все множество, а элемент не будет найден, алгоритм должен выдать отрицательный результат.
Алгоритм последовательного поиска
Шаг 1. Полагаем, что значение переменной цикла i=0.
Шаг 2. Если значение элемента массива x[i] равно значению ключа key, то возвращаем значение, равное номеру искомого элемента, и алгоритм завершает работу. В противном случае значение переменной цикла увеличивается на единицу i=i+1.
Шаг 3. Если i<k, где k – число элементов массива x, то выполняется Шаг 2, в противном случае – работа алгоритма завершена и возвращается значение равное -1.
При наличии в массиве нескольких элементов со значением key данный алгоритм находит только первый из них (с наименьшим индексом).
int LinearSearch(int *x, int k, int key){
int i = 0;
for ( i = 0 ; i < k ; i++ )
if ( x[i] == key )
break;
return i < k ? i : -1;
}Время выполнения данного алгоритма поиска для вещественных чисел  , где n – количество элементов множества, а
, где n – количество элементов множества, а  – точность. Поиск на дискретном множестве из n элементов осуществляется в худшем случае за n итераций, а в среднем этот алгоритм требует n/2 итераций цикла. Следовательно, временная сложность последовательного поиска пропорциональна O(n). Никаких ограничений на порядок элементов в массиве данный алгоритм не накладывает.
– точность. Поиск на дискретном множестве из n элементов осуществляется в худшем случае за n итераций, а в среднем этот алгоритм требует n/2 итераций цикла. Следовательно, временная сложность последовательного поиска пропорциональна O(n). Никаких ограничений на порядок элементов в массиве данный алгоритм не накладывает.
Недостатком рассматриваемого алгоритма поиска является то, что в худшем случае осуществляется просмотр всего массива. Поэтому данный алгоритм используется, если множество содержит небольшое количество элементов.
Достоинства последовательного поиска заключаются в том, что он прост в реализации, не требует сортировки значений множества, дополнительной памяти и дополнительного анализа функций. Следовательно, может работать в потоковом режиме при непосредственном получении данных из любого источника.
Существует модификация алгоритма последовательного поиска, которая ускоряет поиск. Эта модификация является небольшим усовершенствованием рассмотренного алгоритма поиска.
Идея поиска с барьером состоит в том, чтобы не проверять каждый раз в цикле условие, связанное с границами множества. Это можно обеспечить, установив в данном множестве так называемый барьер. Под барьером понимается любой элемент, который удовлетворяет условию поиска. Тем самым будет ограничено изменение индекса.
Выход из цикла, в котором теперь остается только условие поиска, может произойти либо на найденном элементе, либо на барьере. Существует два способа установки барьера: дополнительным элементом или вместо крайнего элемента массива.
//описание функции последовательного поиска с барьером
int LinearSearchWithBarrier(int *x, int k, int key){
x = (int *)realloc(x,(k+1)*sizeof(int));
x[k] = key;
int i = 0;
while ( x[i] != key )
i++;
return i < k ? i : -1;
}Заметим, что поиск с барьером работает быстрее, но временная сложность алгоритма остается такой же O(n), где n – количество элементов множества. Гораздо больший интерес представляют методы, не только работающие быстро, но и реализующие алгоритмы с меньшей сложностью.
Бинарный (двоичный) поиск
Бинарный (двоичный, дихотомический) поиск – это поиск заданного элемента на упорядоченном множестве, осуществляемый путем неоднократного деления этого множества на две части таким образом, что искомый элемент попадает в одну из этих частей. Поиск заканчивается при совпадении искомого элемента с элементом, который является границей между частями множества или при отсутствии искомого элемента.
Бинарный поиск применяется к отсортированным множествам и заключается в последовательном разбиении множества пополам и поиска элемента только в одной половине на каждой итерации.
Таким образом, идея этого метода заключается в следующем. Поиск нужного значения среди элементов упорядоченного массива (по возрастанию или по убыванию) начинается с определения значения центрального элемента этого массива. Значение данного элемента сравнивается с искомым значением и в зависимости от результатов сравнения предпринимаются определенные действия. Если искомое и центральное значения оказываются равны, то поиск завершается успешно. Если искомое значение меньше центрального или больше, то формируется массив, состоящий из элементов, находящихся слева или справа от центрального соответственно. Затем поиск повторяется в новом массиве ( рис. 37.1).
Алгоритм бинарного поиска
Шаг 1. Определить номер среднего элемента массива middle=(high+low)/2.
Шаг 2. Если значение среднего элемента массива равно искомому, то возвращаем значение, равное номеру искомого элемента, и алгоритм завершает работу.
Шаг 3. Если искомое значение больше значения среднего элемента, то возьмем в качестве массива все элементы справа от среднего, иначе возьмем в качестве массива все элементы слева от среднего (в зависимости от характера упорядоченности). Перейдем к Шагу 1.
В массиве может встречаться несколько элементов со значениями, равными ключу. Данный алгоритм находит первый совпавший с ключом элемент, который в порядке следования в массиве может быть ни первым, ни последним среди равных ключу. Например, в массиве чисел 1, 5, 5, 5, 5, 5, 5, 7, 8 с ключом key =5 совпадет элемент с порядковым номером 4, который не относится ни к первому, ни к последнему.
Существуют две модификации рассматриваемого алгоритма для поиска первого и последнего вхождения. Все зависит от того, как выбирается средний элемент: округлением в меньшую или большую сторону. В первом случае средний элемент относится к левой части массива, а во втором – к правой.
//описание функции бинарного поиска
int BinarySearch(int *x, int k, int key){
bool found = false;
int high = k - 1, low = 0;
int middle = (high + low) / 2;
while ( !found && high >= low ){
if (key == x[middle])
found = true;
else if (key < x[middle])
high = middle - 1;
else
low = middle + 1;
middle = (high + low) / 2;
}
return found ? middle : -1 ;
}В процессе работы алгоритма бинарного поиска размер фрагмента, где этот поиск должен продолжаться, каждый раз уменьшается примерно в два раза. Это обеспечивает сложность алгоритма пропорциональную O(log n), где n – количество элементов множества.
Время выполнения алгоритма бинарного поиска: если функция имеет вещественный аргумент, найти решение с точностью до  можно за время
можно за время 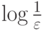 , а если аргумент дискретен, то поиск решения займет 1 + log n времени.
, а если аргумент дискретен, то поиск решения займет 1 + log n времени.
Достоинством данного алгоритма является относительная быстрота выполнения поиска, по сравнению с алгоритмом последовательного поиска. Недостаток заключается в том, что бинарный поиск может применяться только на упорядоченном множестве.
Ключевые термины
Бинарный (двоичный, дихотомический) поиск – это поиск заданного элемента на упорядоченном множестве, осуществляемый путем неоднократного деления этого множества на две части таким образом, что искомый элемент попадает в одну из этих частей.
Ключ поиска – это поле записи, по значению которого происходит поиск
Поиск – это процесс нахождения конкретной информации в ранее созданном множестве данных.
Поиск с барьером – это модификация алгоритма последовательного поиска, ускоряющая процесс путем определения граничного элемента.
Последовательный (линейный) поиск – это простейший вид поиска заданного элемента на некотором множестве, осуществляемый путем последовательного сравнения очередного рассматриваемого значения с искомым до тех пор, пока эти значения не совпадут.
Краткие итоги
- Одним из важнейших действий со структурированной информацией является поиск.
- Существует множество различных алгоритмов поиска, которые принципиально зависят от способа организации данных. У каждого алгоритма поиска есть свои преимущества и недостатки.
- Последовательный (линейный) поиск является простейшим видом поиска заданного элемента на некотором множестве, осуществляемым путем последовательного сравнения очередного рассматриваемого значения с искомым до тех пор, пока эти значения не совпадут.
- Существует модификация алгоритма последовательного поиска, которая ускоряет поиск путем установки в рассматриваемом множестве барьера.
- Бинарный (двоичный, дихотомический) поиск является поиском заданного элемента на упорядоченном множестве, осуществляемым путем неоднократного деления этого множества на две части таким образом, что искомый элемент попадает в одну из этих частей. Бинарный поиск применяется к отсортированным множествам.
- Преимуществом бинарного поиска является более низкая трудоемкость по сравнению с последовательным поиском. Недостаток бинарного поиска состоит в том, что он применим только на отсортированных множествах.

