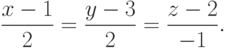|
Можно ли, используя функцию Дирихле, построить модель пространства, в котором нет иррациональных чисел, а есть только рациональные числа? Очевидно, нельзя построить плоскость, не используя при этом иррациональные числа, так как плоскость непрерывна. Но пространство обладает бо-льшим числом измерений и может сохранить непрерывность в каком-либо одном из них. |
Уравнения и неравенства
Плоскость - поверхность (бесконечная в любом направлении), в которой каждая прямая, имеющая две общие точки, целиком лежит на этой поверхности. Из школьной стереометрии известна одна из основных аксиом (стереометрии): существует хотя бы одна прямая и одна плоскость, а каждая прямая и каждая плоскость есть не совпадающее с пространством непустое множество точек, причем прямая, проходящая через две различные точки плоскости, лежит в этой плоскости.
Пусть P - некоторая плоскость, определенная в координатном пространстве.
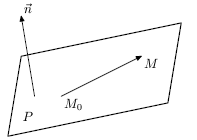
Нормалью к плоскости P называется ненулевой вектор, перпендикулярный к P (нулевой вектор - неинтересен, тривиален, так как он всегда перпендикулярен любому вектору - почему?). Любая плоскость в пространстве однозначно ориентирована, если задана точка 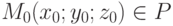 и какой-нибудь вектор нормали n=(A;B;C) к ней (рис. 6.6).
и какой-нибудь вектор нормали n=(A;B;C) к ней (рис. 6.6).
Нужно найти связь между координатами текущей точки M(x; y; z) на P. Так как  , то
, то

 является произвольной, то этому уравнению удовлетворяют все точки на P. Следовательно, это уравнение определяет плоскость, проходящую через точку M0(x0;y0;z0) перпендикулярно к вектору нормали n=(A;B;C).
является произвольной, то этому уравнению удовлетворяют все точки на P. Следовательно, это уравнение определяет плоскость, проходящую через точку M0(x0;y0;z0) перпендикулярно к вектору нормали n=(A;B;C).Теорема Любая плоскость в пространстве определяется уравнением вида: Ax+By+Cz+D=0. Обратно, всякое уравнение такого вида, где хотя бы один из постоянных коэффициентов A, B, C не равен нулю, задает некоторую плоскость в пространстве.
Вместо доказательства этой теоремы рассмотрим полезный (и работающий на понимание теоремы) пример.
Пример.
Возьмем возможные частные случаи этого уравнения:
- если D=0, Ax+By+Cz=0, то плоскость P проходит через точку O(0;0;0).
- если A=0, By+Cz+D=0, то плоскость P параллельна оси Ox (
 .
. - если B=0, Ax+Cz+D=0, то плоскость P параллельна оси Oy (
 .
. - если C=0, Ax+By+D=0, то плоскость P параллельна оси Oz (
 .
. - если A=D=0, By+Cz=0, то плоскость P проходит через ось Ox.
- если B=D=0, Ax+Cz=0, то плоскость P проходит через ось Oy.
- если C=D=0, Ax+By=0, то плоскость P проходит через ось Oz.
- если A=B=0, Cz+D=0, то плоскость P параллельна плоскости xOy.
- если B=C=0, Ax+D=0, то плоскость P параллельна плоскости yOz.
- если A=C=0, By+D=0, то плоскость P параллельна плоскости xOz.
- если A=B=D=0, Cz=0 (z=0), то плоскость P совпадает с плоскостью xOy.
- если A=C=D=0, By=0 (y=0), то плоскость P совпадает с плоскостью xOz.
- если B=C=D=0, Ax=0 (x=0), то плоскость P совпадает с плоскостью yOz.
Сделайте графические иллюстрации (рисунки) к каждому случаю самостоятельно.
Пусть заданы плоскости P1 и P2 в пространстве своими общими уравнениями P1: A1x+B1y+C1z+D1=0, P2: A2x+B2y+C2z+D2=0.
Эти плоскости будут коллинеарны (параллельны), если коллинеарны будут их нормали, и перпендикулярны (ортогональны), если будут ортогональны их нормали. Из условий коллинеарности и ортогональности векторов получаем соответствующие условия параллельности и перпендикулярности двух плоскостей:  , A1A2 + B1B2 + C1C2 =0.
, A1A2 + B1B2 + C1C2 =0.
Направляющим вектором для прямой (или направляющим вектором прямой)  называется любой вектор, коллинеарный данной прямой. Часто в качестве направляющего вектора берется единичный вектор (орт) данного направления.
называется любой вектор, коллинеарный данной прямой. Часто в качестве направляющего вектора берется единичный вектор (орт) данного направления.
Любая прямая  определяется однозначно заданием какой-то точки
определяется однозначно заданием какой-то точки 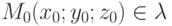 и направляющего вектора S=(m;n;p) прямой
и направляющего вектора S=(m;n;p) прямой  . Найдем уравнение
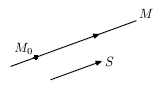
. Найдем уравнение  (рис. 6.7). Пусть точка M(x;y;z) - текущая точка. Тогда M0M =(x-x0; y-y0; z-z0). Так как вектор M0M коллинеарен вектору S, то из условия коллинеарности векторов находим
(рис. 6.7). Пусть точка M(x;y;z) - текущая точка. Тогда M0M =(x-x0; y-y0; z-z0). Так как вектор M0M коллинеарен вектору S, то из условия коллинеарности векторов находим
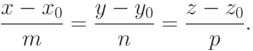
Это уравнение определяет  и называется каноническим уравнением прямой. Пусть точки M1(x1;y1;z1),
и называется каноническим уравнением прямой. Пусть точки M1(x1;y1;z1), 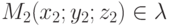 . Тогда за направляющий вектор можно взять M0M =(x2-x1; y2-y1; z2-z1) =S.
. Тогда за направляющий вектор можно взять M0M =(x2-x1; y2-y1; z2-z1) =S.
Из предыдущего уравнения получим (полагая  ) соотношение вида
) соотношение вида
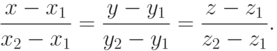
Это уравнение определяет прямую, проходящую через две точки M1, M2, и называется каноническим уравнением прямой в пространстве.
Пример. Если даны две точки A(1;3;2) и B(3,5,1), то в качестве направляющего вектора прямой, проходящей через эти точки, можно взять вектор AB(2; 2; -1). Уравнение прямой имеет вид