НОУ ИНТУИТ | Введение в математику. Лекция 5: Графы и их использование

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 18.04.2007 | Уровень: для всех | Доступ: свободно | ВУЗ: Кабардино-Балкарский государственный университет

Сетевой график представляет собой некоторый ориентированный взвешенный граф, при построении которого соблюдены нижеследующие правила:

задано множество событий (операций) некоторого проекта, комплекса работ и множество ребер графа. Ребро (дуга), ведущая из события (вершины) с номером i в событие (вершину) с номером j, идентифицируется с длительностью работы по переходу от события i к событию j ;
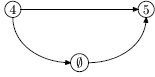
никакие две работы не могут быть идентифицированы одними событиями; это условие может быть всегда выполнено путем введения фиктивных событий (событий, не требующих ни времени, ни ресурсов), например, не удовлетворяющая данному условию часть графа

может быть преобразована введением фиктивного события k:
соотношения предшествования/следования должны соблюдаться на всем протяжении сети, то есть выполнение последующей работы не может быть начато, пока не будут завершены все предыдущие работы, причем эта работа не обязательно должна начинаться сразу же после завершения непосредственно предыдущей;
начатая работа должна быть продолжена без перерыва до ее завершения;
при переходе от одной работы к другой не допускаются случайные, вероятностные решения (ветвления);
нумерация работ должна производиться так, чтобы дуга (работа), ведущая из одного узла (события) в другой узел, начиналась из узла с меньшим номером; этого легко можно добиться с помощью следующего алгоритма (нумерации событий): а) присвоить начальному событию номер 1; б) присвоить следующий номер любому ненумерованному событию, для которого все предшествующие события перенумерованы; в) если все события не перенумерованы, то перейти к пункту б), иначе - закончить нумерацию.

Таким образом, сетевой график определяется заданием: перечня всех операций проекта, плана; времени, необходимого для выполнения каждой операции проекта; перечня операций, непосредственно предшествующих каждой операции данного перечня.

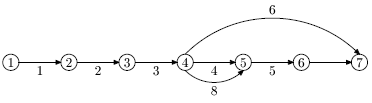
Пример.Строительство нового дома включает укрупненные операции, приведенные в таблице. Сетевой график строительства этого дома (укрупненного проекта) изображен в таблице "Проект строительства дома".

Проект строительства дома
№	Операция	Время (дни)	Предшествующие операции	Дуга графа
1.	Расчистка участка	1	нет	1-2
2.	Закладка фундамента	4	Расчистка участка (1)	2-3
3.	Возведение стен	4	Закладка фундамента (2)	3-4
4.	Монтаж электропроводки	3	Возведение стен (3)	4-5
5.	Штукатурные работы	4	Монтаж электропроводки (4)	3-6
6.	Благоустройство территории	6	Возведение стен (3)	5-7
7.	Отделка	4	Штукатурные работы (5)
8.	Настил крыши	5	Возведение стен (3)	3-8

Рис. 5.5. Сетевой график проекта строительства дома

Две работы, соответствующие дуге 4-5, - параллельные, их можно либо заменить одной, представляющей совместную операцию (монтаж электропроводки и настил крыши), с новой длительностью 3+5=8, либо ввести на одной дуге фиктивное событие, например, событие $\emptyset$ ; тогда дуга 4-5 примет вид

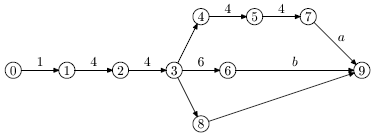
Часто при изображении сетевого графика дуги снабжают весами (длительностями, ресурсами и т.п.) работ. В соответствии с этим принципом, предыдущий сетевой график будет иметь вид, изображенный на рис. 5.6.

Рис. 5.6. Сетевой график проекта строительства дома с весами

Здесь введены два события: 0 - начало строительства дома, 9 - завершение (сдача) дома. Длительности a, b, c работ 7-9, 6-9, 8-9 должны быть определены.

Критическим путем сетевого графика называется любой путь (то есть последовательность взаимосвязанных событий), ведущий из начального события в конечное событие и целиком состоящий из работ, задержка которых на время $\Delta t$ вызовет задержку окончания всего проекта на $\Delta t$ времени. Таким образом, для своевременного окончания проекта все события на критическом пути должны быть выполнены без задержек. Критический путь может быть определен как путь из начального в конечное событие, имеющий нулевой резерв времени (нет резерва времени).

Для нахождения критического пути на сетевом графике необходимо оценить резервы времени (ресурсов) для событий (работ) графика: определить для каждого события наиболее ранний и наиболее поздний сроки его наступления (из всех возможных, допускающих окончание всего проекта в срок).

Наиболее ранний срок наступления события j определяется как продолжительность самого длинного пути от начального события к конечному. Пусть t_ij - время, необходимое для выполнения работы (i,j), то есть работы по переходу от события i к событию j. Пусть от начального события (i=1) к j -му событию ведут k путей, которые мы обозначим через 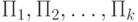$\Pi_1, \Pi_2, \dotsc, \Pi_k$ . Продолжительность всех работ на пути 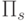$\Pi_s$ состоит из суммы продолжительностей, составляющих этот путь 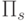$\Pi_s$ работ:

$T_m(\Pi_s) = \SUM_{p\in \Pi_s} \SUM_{q\in \Pi_s} t_{pq}, \quad$

s= 1,2,..., k, m=1, 2,...,n.

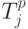Пусть T_j^p - наиболее ранний срок наступления события j, $1\le j\le n$ . Он определяется как самый длинный путь от первого узла (i=1) до j -го узла:

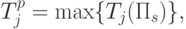
$T^p_j=\max \{T_j(\Pi_s)\},$

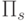j=1,2,...,n. Максимум берется по всем путям $\Pi_s$ , соединяющим узлы 1 и j. Следовательно,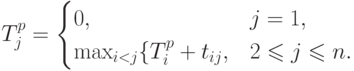

$T^p_j = \begin{cases} 0, & j=1, \\ \max_{i<j} \{T^p_i +t_{ij}, & 2\le j\le n. \end{cases}$

Максимум берется по всем работам, завершающимся в j -ом узле и выходящим из любого предшествующего i -го узла.

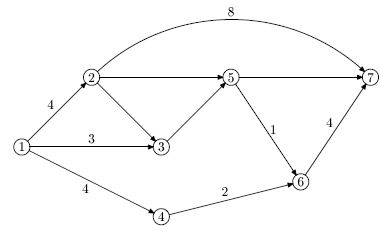
Пример. Рассмотрим сетевой график, изображенный на рис. 5.7.

Рис. 5.7. Сетевой график для примера

Для этого сетевого графика получаем: $\aligned & T_1^p=0, \\[2pt] & T_2^p=T_1^p+t_{12}=0+4=4, \\[2pt] & T_3^p=\max \{T_1^p+t_{13}, T_2^p+t_{23}\}=\max \{4+1{,}0+3\}=5, \\[2pt] & T_4^p=T_1^p+t_{14}=0+4=4, \\[2pt] & T_5^p=\max \{T_2^p+t_{25}, T_3^p+t_{35}\}=\max \{4+7{,}5+4 \}=11, \\[2pt] & T_6^p=\max \{T_4^p+t_{46}, T_5^p+t_{56}\}=\max \{4+2{,}11+1\}=12, \\[2pt] & T_7^p=\max \{T_2^p+t_{27}, T_5^p+t_{57}, T_6^p+t_{67}\}=\max \{4+8{,}11+3{,}12+4\}=16. \endaligned$

Определим теперь понятие наиболее позднего срока наступления события. Пусть 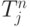T_j^n - наиболее поздний срок наступления i -го события, не отодвигающий время завершения всего проекта, то есть наиболее поздний срок завершения всех работ, ведущих к i -му узлу. Тогда ясно, что наиболее поздний срок наступления последнего события n (завершения проекта) необходимо положить равным наиболее раннему сроку завершения проекта. Это нужно для того, чтобы гарантировать, что самый длинный путь (критический) не будет требовать времени больше заданного времени завершения проекта. Следовательно, 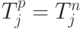T_j^p =T_j^n . Чтобы определить наиболее поздний срок наступления любого события i (i<n), необходимо делать просчет в обратном направлении. Пусть i -му событию предшествует ряд работ. Вычислим наиболее поздние сроки наступления всех событий, предшествующих i -му событию, и вычтем продолжительности работ, ведущих в i -ое событие. Тогда

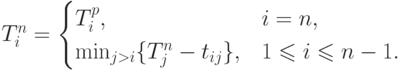
$T_i^n = \begin{cases} T^p_i, & i=n, \\ \min _{j>i} \{T^n_j - t_{ij}\}, & 1\le i\le n-1. \end{cases}$

Минимум берется по всем событиям, соединенным с i -ым событием.

Пример. Для сетевого графика 5.7 имеем: $\begin{aligned} &T_7^n=T_7^p=16, \\[2pt] &T_6^n=T_7^n-t_{67}=16-4=12, \\[2pt] &T_5^n=\min\{T_7^n- t_{57},T_6^n-t_{56}\}=\min\{16-3,12-1\}=11, \\[2pt] &T_4^n=T_6^n-t_{46}=12-2=10, \\[2pt] &T_3^n=T_5^n-t_{35}=11-4=7, \\[2pt] &T_2^n=\min\{T_7^n-t_{27},T_5^n-t_{25},T_3^n-t_{23}\}=\min\{16-8{,}11-7{,}7-1\}=4, \\[2pt] &T_1^n=\min\{T_4^n-t_{14},T_3^n-t_{13},T_2^n-t_{12}\}=\min\{10-4,7-3,4-4\}=0. \end{aligned}$ Таким образом, чтобы закончить этот проект в момент времени t=16, необходимо его начать в момент времени t=0.

Итак, 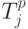T_j^p - длина пути наибольшей длительности от события 1 к событию i, а T^n_n-T_j^n - длина пути наибольшей длительности от события i к событию n. Эти длины определяются взятием максимума (минимума).

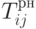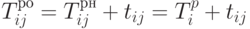Пусть теперь $T_{ij}^{\text{рн}}$ - наиболее ранний возможный срок начала работы (i,j) (далее мы будем обозначать просто ij ). Так как работа не может начинаться раньше наступления предшествующего i, то имеем: $T_{ij}^{\text{рн}}=T_j^p$ . Поэтому наиболее ранний возможный срок окончания работы ij будет равен: $T_{ij}^{\text{ро}} = T_{ij}^{\text{рн}} + t_{ij}= T^p_i +t_{ij}$ .

Наиболее поздний допустимый срок окончания работы - самое позднее время завершения работы, гарантирующее завершение всего проекта без задержки. Так как работу ij можно закончить не позже наиболее позднего допустимого срока наступления последнего события j, то полагаем: 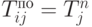$T_{ij}^{\text{по}}= T^n_j$ .

Наиболее поздний срок начала работы ij: 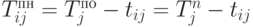$T_{ij}^{\text{пн}} = T_j^{\text{по}}-t_{ij} = T_j^n - t_{ij}$ .

Определим теперь резервы времени. Пусть R_i - резерв времени для выполнения i -го события. Тогда 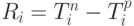R_i=T_i^n-T^p_i . Если T_i^n=T^p_i , то задержка события i не допускается. События с нулевым резервом времени (R_i=0) называются критическими событиями . Эти события находятся на критическом пути; все события критического пути имеют нулевой резерв времени. Работы, не находящиеся на критическом пути, также могут иметь нулевой резерв. 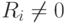На пути, не являющемся критическим, можно осуществить задержку некоторых работ (с $R_i\ne 0$ ) без ущерба времени окончания всего проекта. Сократить срок завершения всего проекта можно только сокращением сроков выполнения работ, находящихся на критическом пути.

Полный (суммарный) резерв времени работы ij, которая не вызовет задержки окончания всего проекта:

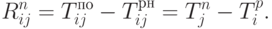
$R_{ij}^n = T_{ij}^{\text{по}} - T_{ij}^{\text{рн}} = T^n_j - T^p_i.$

Работа ij с R_ij=0 находится на критическом пути.

Свободный ( частный ) резерв времени является показателем максимальной задержки работы ij, не влияющей на начало последующих работ jk, $k\le n$ . Свободный резерв времени отличается от суммарного резерва времени тем, что он измеряет имеющееся время (резерв), не влияющее на задержку последующих работ. Он равен:

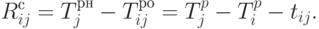
$R_{ij}^{\text{с}} = T_j^{\text{рн}} - T_{ij}^{\text{ро}} = T^p_j - T^p_i -t_{ij}.$

Независимый резерв времени работы ij - это максимальная продолжительность задержки работы ij без задержки последующих работ, при условии, что все предшествующие работы заканчиваются как можно позже. Этот резерв показывает время, которое необходимо для наихудшего состояния выполнения всех работ, предшествующих работе ij:

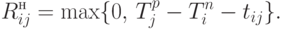
$R_{ij}^{\text{н}}=\max \{0,\, T_j^p - T^n_i - t_{ij}\}.$

Для примера (рис. 5.7), приведенного выше, получаем таблицу резервов времени.

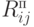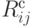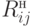Событие	Операция	$R_{ij}^{\text{п}}$	$R_{ij}^{\text{с}}$	$R_{ij}^{\text{н}}$
1.	(1,2)	4-0-4=0	4-0-4=0	4-0-4=0
2.	(1,3)	7-0-3=4	5-0-3=2	5-0-3=2
3.	(1,4)	10-0-4=6	4-0-4=0	4-0-4=0
4.	(2,3)	7-4-1=2	5-4-1=0	5-4-1=0
5.	(2,5)	11-4-7=0	11-4-7=0	11-4-7=0
6.	(2,7)	16-4-8=4	16-4-8=4	16-4-8=4
7.	(3,5)	11-5-4=2	11-5-4=2	11-7-4=0
8.	(4,6)	12-4-2=6	12-4-2=6	12-10-2=0
9.	(5,6)	12-11-1=0	12-11-1=0	12-11-1=0
10.	(5,7)	16-11-3=2	16-11-3=2	16-11-3=2
11.	(6,7)	16-12-4=0	16-12-4=0	16-12-4=0

Дальше >>

Введение в математику

Графы и их использование

Вопросы и ответы

Студенты

Авторизоваться

Введение в математику

Графы и их использование

Вопросы и ответы

Студенты