| Россия, г. Краснотурьинск |
Методы и модели разработки управленческих решений в сервисной деятельности
Виды задач принятия управленческих решений, методы их разработки
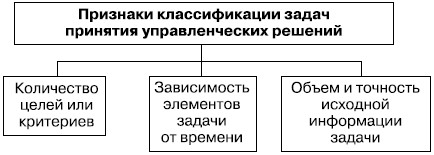
Признаки классификации задач принятия управленческих решений. Классифицирование задач принятия решений по видам представляет собой процесс их упорядочивания по выбранным признакам с соблюдением действующей закономерности перехода от одного вида к другому. В результате этого удается не только глубже познать эту закономерность, но и распределить множество всех задач по видам и для каждой из них обосновать применение того или иного метода разработки решений. Признаки классификации задач принятия управленческих решений представлены на рис. 27.11.
- Количество целей или критериев, которым должны удовлетворять разрабатываемые решения. По этому признаку задачи делят на одноцелевые, илиоднокритериальные (в постановке задачи формулируется единственный критерий выбора решения), и многоцелевые, илимногокритериальные (в постановке задачи формулируется более одного критерия, т. е. два, три и т. д. , которые должны быть достигнуты одновременно).
- Зависимость параметров задачи от времени. По принятому допущению, вводимые в задачу параметры могут оставаться постоянными, т. е. не зависящими от времени, либо, наоборот, меняться с течением времени. В первом случае, когда параметры считаются неизменными на протяжении рассматриваемого периода, задача называется статической, во втором, когда параметры являются функциями времени ("плывут"), - динамической.
- Объем и точность исходной информации задачи.
Виды задач принятия управленческих решений. В соответствии с рассмотренными выше условиями объема и точности исходной информации, задачи классифицируют следующим образом:
- задачи в условиях определенности (детерминированные) - существует однозначная связь между принятым решением и результатом его выполнения, поэтому используются традиционные детерминированные методы, широко распространенные в экономических исследованиях; в частности, для наиболее распространенных среди детерминированных задач - задач статических - применяют математический анализ, линейную алгебру, методы математического (линейного, нелинейного, дискретного и др.) программирования и иные методы;
- задачи в условиях риска (вероятностные, или стохастические) - из-за необходимости учета случайных факторов формальным аппаратом служат разделы математики, оперирующие случайными величинами, - теории вероятностей и массового обслуживания, математическая статистика, метод Монте-Карло и др.;
- задачи в условиях неопределенности - применяются специально разработанные игровые методы. Они обосновывают предпочтительные стратегии для участников, цели которых не совпадают в тех или иных ситуациях (называемых поэтому конфликтными задачами). Наряду с этим задачи в условиях риска и неопределенности могут потребовать привлечения эвристических процедур, опирающихся на суждения квалифицированных специалистов-экспертов.
Классификация однокритериальных задач принятия управленческих решений и методов их поиска приведена в табл. 27.1.
| Метод | Задачи принятия решения в условиях | ||
| определенности | риска | неопределенности | |
| Статические | Методы математического анализа, линейной алгебры и математического программирования | Методы теории вероятностей и массового обслуживания, Монте-Карло, математического программирования, эвристические методы | Методы теории статистических решений, теории игр, минимакса, эвристические методы |
| Динамические | Методы теории оптимальных процессов (вариационное исчисление и др.) | Методы теории случайных процессов, статистической динамики систем управления, эвристические методы | Методы теории дифференциальных игр, эвристические методы |
Многокритериальные задачи используют методы активно развивающейся ныне теории многокритериальных задач, "дерева целей" и эвристические процедуры.
Оценивая сложность задач принятия решений, можно заметить, что наиболее простыми и изученными из них являются однокритериальные статические детерминированные задачи, наиболее сложными - задачи в условиях неопределенности и многокритериальные задачи.
Проблемы в процессе постановки задачи и поиска управленческих решений. В ходе формулирования постановки задачи и разработки управленческих решений появляются проблемы как концептуального, так и формально-математического и вычислительного характера. Первые связаны с трудностями осознания сути возникшей ситуации, установления факторов и целей деятельности предприятия. Такие плохо понимаемые и слабо структурированные ситуации подвергаются анализу на уровне руководства предприятия с участием консультантов.
Обычно для концептуального осмысления сложной ситуации проводят диагностику, выявляют ее причины и раскрывают сущность. Затем, по мере накопления информации и углубления знаний о ситуации, исследуют механизм ее развития и возможные последствия. Очевидно, что подобного рода проблемы, ориентирующие на творческий поиск и генерацию идей, присущи прежде всего задачам в условиях риска, неопределенности и многокритериальным задачам.
Проблемы формально-математического и вычислительного характера порождаются трудностями выбора или построения алгоритма решения задачи, перевода ее на математический язык и компьютеризации (программирования, отладки, сопровождения задачи и т. д.). В данном случае усилия направлены на конструирование адекватного и удобного инструмента для разработки предпочтительного решения с использованием современных компьютерных технологий. Эти проблемы свойственны однокритериальным детерминированным задачам и находятся в компетенции математиков, аналитиков, программистов, информационных технологов и др.