| Казахстан |
Контрастирование (редукция) нейронной сети
Сокращение числа выходов в адаптивном линейном сумматоре (путь "снизу вверх")
Рассмотрим адаптивный линейный сумматор, вычисляющий линейную функцию  .
.
Решим задачу о сокращении числа выходных сигналов. Рассмотрим определение значимости по изменению выходного сигнала. Заметим, что:

Уничтожить  -й выходной сигнал можно двумя способами:
-й выходной сигнал можно двумя способами:
- заменой параметра
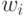 на 0;
на 0; - заменой
 на постоянную величину не зависящую от
на постоянную величину не зависящую от  .
.
В последнем случае получаем новую функцию

Такое преобразование означает, что одновременно с уничтожением  -й
выходной связи
-й
выходной связи 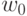 приобретает новое значение:
приобретает новое значение:
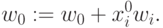
При этом можно добиться меньшего изменения  , чем просто
при
приравнивании
, чем просто
при
приравнивании 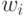 к нулю. Поэтому остановимся на замене
к нулю. Поэтому остановимся на замене  -го выходного
сигнала на постоянную величину
-го выходного
сигнала на постоянную величину 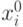 . Значение этой постоянной
определим
исходя из минимизации изменения
. Значение этой постоянной
определим
исходя из минимизации изменения 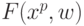 . Минимизация этого
изменения,
вычисленного в евклидовой норме, дает:
. Минимизация этого
изменения,
вычисленного в евклидовой норме, дает:
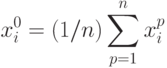
Таким образом, оптимальной является замена  на его среднее
значение по
исходной выборке. В обозначениях теории вероятностей:
на его среднее
значение по
исходной выборке. В обозначениях теории вероятностей:

где 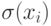 - среднеквадратичное отклонение от
- среднеквадратичное отклонение от 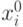 на выборке
на выборке 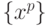 .
.
Значимость замены оценивается как

При исключении сигналов по одному, они сортируются в соответствии со
значениями 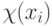 и отбрасываются (заменяются средним)
сначала те, что
соответствуют меньшим
и отбрасываются (заменяются средним)
сначала те, что
соответствуют меньшим 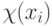 . Заметим, что поэтому путь
"снизу вверх"
универсален, но не оптимален. В частности, для сумматоров и других
элементов, линейных по параметрам (например, квадратичных сумматоров),
существует учитывающий все корреляции путь исключения "сверху
вниз" с
ортогонализацией. Далее ограничимся оценкой значимости по изменению
выходного сигнала.
. Заметим, что поэтому путь
"снизу вверх"
универсален, но не оптимален. В частности, для сумматоров и других
элементов, линейных по параметрам (например, квадратичных сумматоров),
существует учитывающий все корреляции путь исключения "сверху
вниз" с
ортогонализацией. Далее ограничимся оценкой значимости по изменению
выходного сигнала.
