| Казахстан |
Контрастирование (редукция) нейронной сети
Определение значимости параметров по изменению выходных сигналов системы
Значимость параметров определяется практически так же, как и с помощью
функции оценки. Пусть  - вектор данных, а
- вектор данных, а  -
вектор параметров. Пусть задан набор векторов
-
вектор параметров. Пусть задан набор векторов 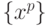 , на которых будет оцениваться
функционирование
системы, и определены значения
, на которых будет оцениваться
функционирование
системы, и определены значения 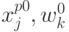 (в простейшем
случае
(в простейшем
случае 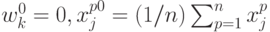 ).
).
Вычислим в линейном приближении изменение вектора  при
обращении
при
обращении 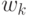 в
в 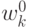 и
и 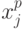 в
в 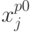 :
:
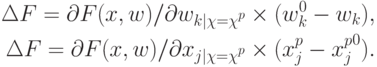
Пусть в пространстве выходных сигналов системы задана некоторая норма (например, евклидова). Тогда положим:
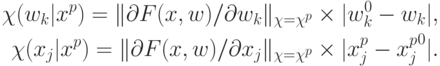
Таким образом, для каждого 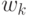 и любого
и любого  определен вектор показателей
значимости. Координаты вектора соответствуют точкам
определен вектор показателей
значимости. Координаты вектора соответствуют точкам 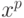 . Теперь
нужно
вычислить норму этого вектора и объявить ее показателем значимости (можно
в качестве нормы взять максимум модуля или сумму модулей). При
использовании евклидовой нормы в пространстве выходных сигналов бывает
удобно и далее выбирать такую же норму, полагая:
. Теперь
нужно
вычислить норму этого вектора и объявить ее показателем значимости (можно
в качестве нормы взять максимум модуля или сумму модулей). При
использовании евклидовой нормы в пространстве выходных сигналов бывает
удобно и далее выбирать такую же норму, полагая:

Подход к определению значимости через изменение выходного сигнала не имеет альтернатив в том случае, когда рассматриваемая система является лишь подсистемой в некоторой системе (например, сумматор или нейрон в нейронной сети). Тогда при изменении параметров этой подсистемы приходится ограничиться требованием: выходной сигнал подсистемы должен изменяться как можно меньше, чтобы не нарушать функционирование всей системы.
