| Казахстан |
Виды нейронных сетей и способы организации их функционирования
Оценка способности сети решить задачу
В данном разделе рассматриваются только сети, все элементы которых
непрерывно зависят от своих аргументов. Предполагается, что все входные
данные предобработаны так, чтобы все входные и выходные сигналы сети
лежали в диапазоне приемлемых входных сигналов ![[a,b].](/sites/default/files/tex_cache/d5f1c430bf683ed676382edef55aa192.png)
Нейронная сеть вычисляет некоторую вектор-функцию  от входных
сигналов.
Эта функция зависит от параметров сети. Обучение сети состоит в подборе
такого набора параметров сети, чтобы величина
от входных
сигналов.
Эта функция зависит от параметров сети. Обучение сети состоит в подборе
такого набора параметров сети, чтобы величина
![\sum_{i,p}[F_i(x^p) - f_i^p]^2](/sites/default/files/tex_cache/9a266d519d9fcc2096bd70fdbdc2ac88.png)
была минимальной (в идеале равна нулю), здесь 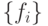 - множество
аппроксимируемых функций. Для того, чтобы нейронная сеть могла хорошо
приблизить заданную таблично функцию
- множество
аппроксимируемых функций. Для того, чтобы нейронная сеть могла хорошо
приблизить заданную таблично функцию  , необходимо, чтобы
реализуемая
сетью функция
, необходимо, чтобы
реализуемая
сетью функция  при изменении входных сигналов с
при изменении входных сигналов с 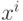 на
на 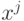 могла
изменить значение с
могла
изменить значение с 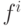 на
на 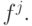 Очевидно, что
наиболее трудным для
сети должно быть приближение функции в точках, в которых при малом
изменении входных сигналов происходит большое изменение значения функции.
Таким образом, наибольшую сложность будет представлять приближение функции
Очевидно, что
наиболее трудным для
сети должно быть приближение функции в точках, в которых при малом
изменении входных сигналов происходит большое изменение значения функции.
Таким образом, наибольшую сложность будет представлять приближение функции  в точках, в которых достигает максимума выражение
в точках, в которых достигает максимума выражение  Для аналитически заданных функций величина
Для аналитически заданных функций величина
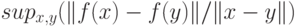
называется константой Липшица. Исходя из этих соображений, можно дать следующее определение сложности задачи.
Сложность аппроксимации таблично заданной функции  , которая в
точках
, которая в
точках 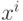 принимает значения
принимает значения 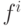 , задается выборочной оценкой константы Липшица, вычисляемой
по формуле:
, задается выборочной оценкой константы Липшица, вычисляемой
по формуле:
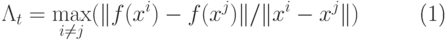 |
( 1) |
Оценка (1) является оценкой константы Липшица аппроксимируемой функции снизу.
Константа Липшица сети вычисляется по следующей формуле:
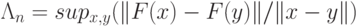
Для того, чтобы оценить способность сети заданной конфигурации решить
задачу, необходимо оценить константу Липшица сети и сравнить ее с
выборочной оценкой (1). В случае  сеть
принципиально не способна решить задачу аппроксимации функции
сеть
принципиально не способна решить задачу аппроксимации функции 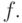 Однако
из
Однако
из 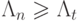 еще не следует утверждение о
способности
сети аппроксимировать функцию
еще не следует утверждение о
способности
сети аппроксимировать функцию  !
!
Константа Липшица сигмоидальной сети
Рассмотрим слоистую сигмоидальную сеть (сеть с сигмоидальными нейронами) со следующими свойствами:
- Число входных сигналов -
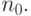
- Число нейронов в
 -м слое -
-м слое - 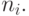
- Каждый нейрон первого слоя получает все входные сигналы, а каждый нейрон любого другого слоя получает сигналы всех нейронов предыдущего слоя.
- Все нейроны всех слоев имеют одинаковые функции активации
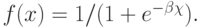
- Все синаптические веса ограничены по модулю единицей.
- В сети
 слоев.
слоев.
В этом случае оценка константы Липшица сети равна:
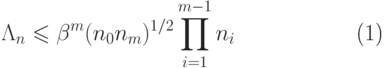 |
( 2) |
Формула (2) подтверждает экспериментально установленный факт, что, чем
круче характеристическая
функция нейрона (т.е. чем больше  ), тем более сложные
функции (функции с большей
константой Липшица) может аппроксимировать сеть с такими нейронами.
), тем более сложные
функции (функции с большей
константой Липшица) может аппроксимировать сеть с такими нейронами.
