| Казахстан |
Виды нейронных сетей и способы организации их функционирования
Предобработка данных
Нормировка и центрирование данных (предобработка) используются почти
всегда (кроме тех случаев,
когда данные представляют собой бинарные векторы с координатами 0,1 или  , либо символьные
последовательности). Цель этих преобразований - сделать так, чтобы каждая
компонента вектора
данных лежала в отрезке
, либо символьные
последовательности). Цель этих преобразований - сделать так, чтобы каждая
компонента вектора
данных лежала в отрезке ![[-1,1]](/sites/default/files/tex_cache/d060b17b29e0dae91a1cac23ea62281a.png) (или
(или ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) ) или,
по крайней мере, не слишком далеко выходила из этого отрезка, и её характерный
разброс тоже был бы единичным.
) или,
по крайней мере, не слишком далеко выходила из этого отрезка, и её характерный
разброс тоже был бы единичным.
Стандартные преобразования исходной выборки 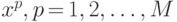 :
:
![x_i^p =[x_i^p - M(x_i^p)]/ \sigma(x_i^p)](/sites/default/files/tex_cache/6c1f95c750b3169b1849c47dd3780994.png) или
или ![x_i^p
=[x_i^p -
M(x_i^p)]/ max | x_i^p - M(x_i^p)|,](/sites/default/files/tex_cache/2fc8012e75ccfd7c41c751b1d879d162.png) где
где  -
-  -я компонента
вектора
-я компонента
вектора 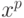 ,
,
 - выборочная оценка математического
ожидания
- выборочная оценка математического
ожидания  ;
;
![\sigma(x_i^p) = \{\sum_i^p[x_i^p - M(x_i^p)]^2/n\}^{1/2}](/sites/default/files/tex_cache/2a403ef4ae171c9f1fa140191f70c683.png) -
выборочная
оценка среднего квадратичного отклонения. Любое изменение выборки
-
выборочная
оценка среднего квадратичного отклонения. Любое изменение выборки 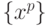 должно, согласно этим формулам, менять
и нормировку. Нормировка и центрирование вписывают исходную выборку в куб со
стороной 2,
вершинами которого являются векторы с координатами
должно, согласно этим формулам, менять
и нормировку. Нормировка и центрирование вписывают исходную выборку в куб со
стороной 2,
вершинами которого являются векторы с координатами 
Интерпретация ответов сети
При интерпретации выходных сигналов сети необходимы аккуратность и порой изобретательность, ведь от этого истолкования зависят требования, которые мы предъявляем к работе НС. Удачная их формулировка может упростить обучение и повысить точность работы, неудачная — свести на нет предыдущие усилия.
Масштабирование является
естественной операцией при обработке
выходных сигналов. Стандартные (обезразмеренные) НС формируются так,
чтобы их выходные сигналы лежали в интервалах ![[-1,1]](/sites/default/files/tex_cache/d060b17b29e0dae91a1cac23ea62281a.png) (или
(или ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) ). Если
нам нужно получить сигнал в интервале
). Если
нам нужно получить сигнал в интервале ![[a,b]](/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) , то нужно
преобразовать
выходной сигнал
, то нужно
преобразовать
выходной сигнал ![y\in [-1,1]](/sites/default/files/tex_cache/ad8cdf978960b0ced08ee3aafc8a3822.png) :
:
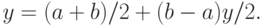
В задачах классификации наиболее распространено правило интерпретации "победитель забирает все": число нейронов равно числу классов, номер нейрона с максимальным сигналом интерпретируется как номер класса. К сожалению, если классов много, то этот наглядный метод является слишком расточительным, потребляет слишком много выходных нейронов.
Знаковая
интерпретация требует только 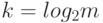 нейронов
(
нейронов
(  -
число классов). Строится она так. Пусть
-
число классов). Строится она так. Пусть  -
совокупность
выходных сигналов нейронов. Заменим в этой последовательности
положительные числа единицами, а отрицательные - нулями. Полученную
последовательность нулей и единиц рассматриваем как номер класса в
двоичной записи.
-
совокупность
выходных сигналов нейронов. Заменим в этой последовательности
положительные числа единицами, а отрицательные - нулями. Полученную
последовательность нулей и единиц рассматриваем как номер класса в
двоичной записи.
Порядковая
интерпретация является еще более емкой, чем
знаковая. В ней с помощью  нейронов можно описать принадлежность
к
нейронов можно описать принадлежность
к  !
классам (а не
!
классам (а не 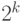 как для знаковой). Пусть
как для знаковой). Пусть 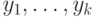 - выходные
сигналы. Проведем их сортировку и обозначим через
- выходные
сигналы. Проведем их сортировку и обозначим через 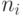 номер
номер  -го
сигнала после сортировки (1 соответствует наименьшему сигналу,
-го
сигнала после сортировки (1 соответствует наименьшему сигналу,  -
наибольшему). Перестановку
-
наибольшему). Перестановку  рассмотрим
как
слово, кодирующее номер класса. Всего возможно
рассмотрим
как
слово, кодирующее номер класса. Всего возможно  ! перестановок.
Этим
интерпретатором можно пользоваться, если характерная ошибка выходного
сигнала меньше
! перестановок.
Этим
интерпретатором можно пользоваться, если характерная ошибка выходного
сигнала меньше 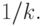 Даже при
Даже при  получаем
реализуемые требования к
точности
получаем
реализуемые требования к
точности 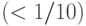 и богатые возможности (10! классов).
и богатые возможности (10! классов).
