НОУ ИНТУИТ | Нейроинформатика. Лекция 3: Быстрое дифференцирование, двойственность и обратное распространение ошибки

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 01.03.2007 | Уровень: специалист | Доступ: свободно

Вам нравится? Нравится 29 студентам

| Поделиться |

Поддержать программу

Сложность вычисления функции и ее градиента

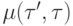Подсчитаем теперь число операций, необходимых для вычисления всех двойственных переменных $\mu (\tau )$ для вершин и $\mu (\tau ', \tau )$ - для ребер.

Во-первых, нужно вычислить все частные производные

${\frac{\partial f^\theta (t_1 ,...,t_k )}{\partial t_i }}$

для всех вершин $\theta$ и всех k аргументов "простой" функции, соответствующей каждой вершине. Число таких производных равно сумме числа аргументов для всех функциональных символов, соответствующих вершинам графа, то есть следующей величине E:

$E = \sum\limits_{(\tau ,\theta ) \in {\rm{e}}(G)}{P(\tau ,\theta )} .$

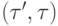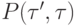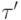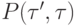Договоримся в этом разделе отображать ребра $(\tau ', \tau )$ , имеющие в своих метках $P(\tau ', \tau )$ больше одного номера, как пучки ребер, идущих от вершины $\tau '$ к вершине $\tau$ - по одному такому ребру для каждого номера из $P(\tau ', \tau )$ . Число E просто равно числу ребер в графе. Число необходимых умножений и число сложений также не превосходят E.

Количество вычислений "простых" функций при вычислении сложной равно числу вершин графа. Обозначим его V. Отношение E/V дает представление об отношении вычислительных затрат на вычисление градиента к затратам на вычисление функции. Чтобы последовательно использовать эту оценку, а также искать те функции, для которых вычисление градиента еще проще, необходимо зафиксировать исходные предположения. Будем обозначать T_f затраты на вычисление f.

Для каждой вершины графа, соответствующей ей функции f, и любого аргумента этой функции x справедлива оценка $T_f \cong T_{\partial f/\partial x}$ ;
Для функций $f=f^\tau (z_1 ,...,z_k )$ , соответствующих вершинам графа, $T_f \ge T_\Sigma ,{\rm{ }}\Sigma = \sum\limits_{i = 1}^k {z_i }$ , то есть сумма переменных - простейшая функция;
Умножение и сложение имеют примерно одинаковую сложность.

В предположениях 1-3 зафиксирован тот уровень точности, с которым будут делаться оценки. При формальном использовании отношения " a примерно равно b " неизбежны парадоксы типа "куча": один камень не куча, если n камней - не куча, то и n+1 - тоже, следовательно... . Чтобы избежать этого и сделать рассуждения более наглядными, поступим следующим образом. Сложность "простой" функции k переменных и любой ее частной производной оценим как ck, где c - некоторая константа, $c \ge 1$ ; сложность суммы k слагаемых (и произведения k сомножителей) определим как k-1. Последнее вычитание единицы имеет смысл при рассмотрении большого числа сумм, содержащих мало слагаемых.

Пусть, как и выше, E - число ребер графа, V - число вершин, V_out - число выходных вершин (им не соответствует ни одной суммы в (6)). Сложность прямого прохождения графа (вычисления функций) оценивается как cE.

Обратное прохождение графа при вычислении градиентов складывается из трех слагаемых:

Вычисление всех частных производных простых функций, соответствующих вершинам графа. Необходимо вычислить E таких производных. Сложность вычисления одной такой производной для вершины 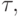$\tau,$ имеющей $|in(\tau )|$ входящих ребер, оценивается как $c|in(\tau )|$ . Оценка сложности вычисления всех этих производных дается следующей суммой
${\rm{T_{Dif} = c}}\sum\limits_\tau {{\rm{|in}}(\tau )|^2 }( \le cE^2 ).$
Вычисление всех произведений (7) на ребрах - E произведений (в связи с тем, что мы в данном разделе передачу сигнала на разные входы автомата, вычисляющего 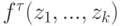$f^\tau (z_1 ,...,z_k )$ , обозначаем различными ребрами, уравнения (7), сохраняя прежнюю внешнюю форму, преобразуются так, что в суммах остается по одному слагаемому, остальное суммирование переносится к вершинам (6)).
Вычисление всех сумм (6) - сложность равна E-(V-V_out).