Статические структуры: классы

Простой класс

Что представляет собой класс можно выяснить, изучая простой, но типичный пример, который демонстрирует фундаментальные свойства, применимые практически ко всем классам.

Компоненты

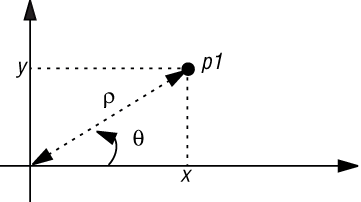
Пример использует представление точки в двумерной графической системе:

Рис. 7.1. Точка и ее координаты

Для определения типа POINT как абстрактного типа данных потребуется четыре функции-запроса: x, y, 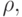(В текстах подпрограмм для двух последних функций будут использоваться имена rho и theta ). Функция x возвращает абсциссу точки (горизонтальную координату), y - ординату (вертикальную координату), - расстояние от начала координат, - полярный угол, отсчитываемый от горизонтальной оси. Значения x и y являются декартовыми, а и - полярными координатами точки. Другой полезной функцией является distance, возвращающая расстояние между двумя точками.

Далее спецификация АТД будет содержать такие команды, как translate (перемещение точки на заданное расстояние по горизонтали и вертикали), rotate (поворот на определенный угол вокруг начала координат) и scale (уменьшение или увеличение расстояния до начала координат в заданное число раз).

Нетрудно написать полную спецификацию АТД, включающую указанные функции и некоторые ассоциированные аксиомы. Далее в качестве примера приведены две из перечисленных функций:

x: POINT -> REAL
translate: POINT x  REAL x  REAL -> POINT

и одна из аксиом:

x (translate (p1, a, b)) = x (p1) + a

утверждающая, что для произвольной точки p1 и действительных значений a и b при трансляции точки на <a, b> абсцисса увеличивается на a.

Читатель, если пожелает, может самостоятельно завершить спецификацию АТД. В дальнейшей дискуссии подразумевается, что вы понимаете, как устроен данный АТД, вне зависимости от того, написали ли вы его полную формализацию или нет. Сосредоточим внимание на реализации АТД - классе.

Атрибуты и подпрограммы

Любой абстрактный тип данных и POINT в частности характеризуется набором функций, описывающих операции применимые к экземплярам АТД. В классе, реализующем АТД, функции становятся компонентами (features) - операциями, применимыми к экземплярам класса.

В "Абстрактные типы данных (АТД)" было показано, что в АТД существуют функции трех видов: запросы (queries), команды (commands) и конструкторы (creators). Для компонентов классов необходима дополнительная классификация, основанная на том, каким образом реализован данный компонент - в пространстве или во времени (by space or by time). (См. "Категории функций", "Абстрактные типы данных (АТД)" )

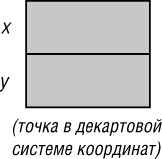
Пример координат точки отчетливо демонстрирует эту разницу. Для точек доступны два общепринятых представления - в декартовых или полярных координатах. Если для представления выбрана декартова система координат, то каждый экземпляр класса содержит два поля представляющих координаты x и y соответствующей точки:

Рис. 7.2. Представление точки в декартовых координатах

Если p1 является такой точкой, то получение значений x и y сведется просто к просмотру соответствующих полей данной структуры. Однако определение значений и требует вычисления выражени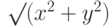я для и arctg (y/x) для (при условии ненулевого x ).

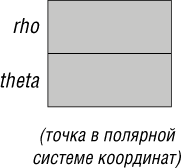
Использование полярной системы координат (рис. 7.3) приводит к противоположной ситуации. Теперь и доступны просто как значения полей, а определение x и y возможно после простых вычислений ( 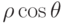, , соответственно).

Рис. 7.3. Представление точки в полярных координатах

Приведенный пример указывает на необходимость рассмотрения компонентов двух видов:

• Некоторые компоненты представлены в пространстве и, можно сказать, ассоциируются с некоторой частью информации каждого экземпляра класса. Они называются атрибутами (attributes). Для точки, представленной в декартовых координатах, атрибутами являются x и y, а в полярных координатах в роли атрибутов выступают rho и theta.
• Другие компоненты представлены во времени, и для доступа к ним требуется описать некоторые вычисления (алгоритмы), применимые далее ко всем экземплярам данного класса. В дальнейшем они называются подпрограммами или методами класса ( routines ). В декартовом представлении точек - rho и theta это подпрограммы, а x и y выступают в качестве подпрограмм при использования полярных координат.

Вторая категория - подпрограммы - нуждается в дальнейшей дополнительной классификации. Часть подпрограмм возвращает результат, и их называют функциями (functions). В приведенном примере функциями являются x и y в представлении в полярных координатах, в то время как rho и theta - функции в декартовых координатах, все они возврвщают результат типа REAL. Подпрограммы, не возвращающие результат, соответствуют командам в спецификации АТД и называются процедурами (procedures). Например, класс POINT содержит процедуры translate, rotate и scale.

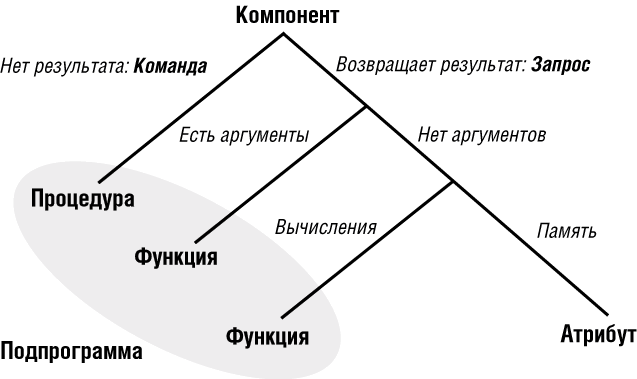
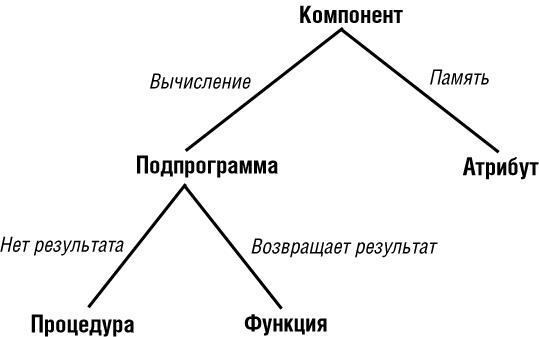
На рис. 7.4 дана рассмотренная выше классификация, представленная в виде дерева:

Рис. 7.4. Классификация компонентов класса по их роли

Эта классификация является внешней, основанной на том, каким образом данный компонент выглядит для использующего его клиента.

Можно предложить другую, внутреннюю классификацию, использующую в качестве основного критерия способ реализации компонента в классе:

Рис. 7.5. Классификация компонентов класса по способу реализации