Абстрактные типы данных (АТД)
Полная спецификация
Раздел ПРЕДУСЛОВИЯ (PRECONDITIONS) завершает простую спецификацию абстрактного типа данных STACK. Для удобства ссылок полезно собрать вместе разные компоненты спецификации, приведенные выше. Вот полная спецификация.
Спецификация стеков как АТД
ТИПЫ (TYPES)
- STACK [G]
ФУНКЦИИ (FUNCTIONS)
- put: STACK [G] x G -> STACK [G]
![remove: STACK [G] \nrightarrow STACK [G]](/sites/default/files/tex_cache/0424f675d30ffaa545850a8f58b9b4a4.png)
![item: STACK [G] \nrightarrow G](/sites/default/files/tex_cache/0b94bb178547b448b5b56f3913068867.png)
- empty: STACK [G] -> BOOLEAN
- new: STACK [G]
Для всех x: G, s: STACK [G]
- (A1) item (put (s, x)) = x
- (A2) remove (put (s, x)) = s
- (A3) empty (new)
- (A4) not empty (put (s, x))
ПРЕДУСЛОВИЯ (PRECONDITIONS)
- remove (s: STACK [G]) require not empty (s)
- item (s: STACK [G]) require not empty (s)
Ничего кроме правды
Сила спецификаций АТД проистекает из их способности отражать только существенные свойства структур данных без лишних деталей. Приведенная выше спецификация стеков выражает все, что нужно по существу знать о понятии стека, и не включает ничего, что относилось бы к каким-либо конкретным реализациям стеков. Это вся правда о стеках, и ничего кроме правды.
Такие спецификации задают общую модель вычислений на соответствующих структурах данных. Определенные в спецификации абстрактного типа данных функции позволяют строить сложные выражения, а аксиомы АТД позволяют упрощать такие выражения и получать более простые результаты. Сложное стековое выражение является математическим эквивалентом программы, а процесс упрощения является математическим эквивалентом вычисления или выполнения этой программы.
Вот пример. Рассмотрим для приведенной выше спецификации АТД STACK следующее выражение stackexp:
item (remove (put (remove (put (put ( remove (put (put (put (new, x1), x2), x3)), item (remove (put (put (new, x4), x5)))), x6)), x7)))
По-видимому, выражение stackexp будет проще понять, если мы представим его как последовательность вспомогательных выражений:
s1 = new s2 = put (put (put (s1, x1), x2), x3) s3 = remove (s2) s4 = new s5 = put (put (s4, x4), x5) s6 = remove (s5) y1 = item (s6) s7 = put (s3, y1) s8 = put (s7, x6) s9 = remove (s8) s10 = put (s9, x7) s11 = remove (s10) stackexp = item (s11)
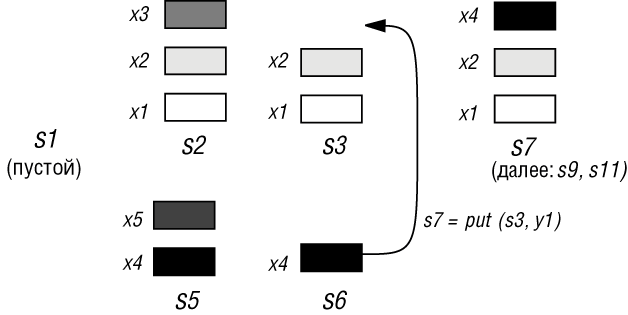
Какой бы вариант определения вы ни выбрали, по нему несложно восстановить вычисление, математической моделью которого является stackexp: создать новый стек; втолкнуть в него элементы x1, x2, x3 (в указанном порядке); удалить верхний элемент (x3), назвав получившийся стек s3; создать другой пустой стек и т. д. Этот процесс графически представлен на рис. 6.5.
Можно легко найти значение такого АТД выражения, нарисовав последовательно несколько таких рисунков. (Здесь найдено x4 ). Но теория позволяет нам получить этот результат формально, не обращаясь к рисункам, а только последовательно применяя аксиомы для упрощения выражения, до тех пор, пока дальнейшее упрощение станет невозможным. Например:
- Применить A2 для упрощения s3 - т. е. заменить remove(put (put (put (s1, x1), x2), x3)) на выражение put (put (s1, x1), x2)). (Согласно A2 всякую пару remove-put можно выбросить).
- По той же аксиоме s6 равно put(s4, x4) . Затем можно применить аксиому A1 и вывести, что y1, т. е. item(put(s4, x4)) на самом деле равно x4, установив тем самым (как указано стрелкой на рисунке), что s7 получается в результате вталкивания x4 на вершину стека s3.
И так далее. Последовательность таких упрощений, выполненная механически так же легко и как последовательность упрощений в элементарной арифметике, приведет к значению выражения stackexp, которое действительно равно x4 (попробуйте проверить это сами, аккуратно проведя весь процесс упрощения).
Этот пример позволяет отметить одну из важнейших теоретических ролей абстрактных типов данных: они предоставляют формальную модель для понятий программы и выполнения программы. Эта модель чисто математическая: в ней нет императивных понятий состояния программы, переменных с изменяемыми во времени значениями, последовательности выполняемых действий. Она основана на обычных математических методах преобразования выражений.