Знакомство с многопоточной обработкой
Задания
- Реализуйте последовательную обработку элементов вектора, например, умножение элементов вектора на число. Число элементов вектора задается параметром N.
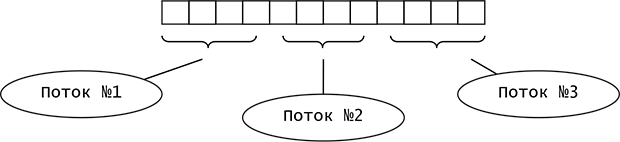
- Реализуйте многопоточную обработку элементов вектора, используя разделение вектора на равное число элементов. Число потоков задается параметром M.
- Выполните анализ эффективности многопоточной обработки при разных параметрах N (10, 100, 1000, 100000) и M (2, 3, 4, 5, 10) Результаты представьте в табличной форме.
- Выполните анализ эффективности при усложнении обработки каждого элемента вектора.
- Исследуйте эффективность разделения по диапазону при неравномерной вычислительной сложности обработки элементов вектора.
- Исследуйте эффективность параллелизма при круговом разделении элементов вектора. Сравните с эффективностью разделения по диапазону.
Методические указания
В работе исследуется эффективность распараллеливания независимой обработки элементов вектора. В первом задании в качестве обработки можно выбрать то или иное математическое преобразование элементов вектора:
for(int i=0; i<a.Length; i++)
b[i] = Math.Pow(a[i], 1.789);
Многопоточная обработка реализуется с помощью объектов Thread. На многоядерной системе многопоточная обработка приводит к параллельности выполнения. Классы для работы с потоками расположены в пространстве имен System.Threading.
Для создания потока необходимо указать имя рабочего метода потока, который может быть реализован в отдельном классе, в главном классе приложения как статический метод или в виде лябда-выражения. Метод потока либо не принимает никаких аргументов, либо принимает аргумент типа object. Запуск потока осуществляется вызовом метода Start.
class Program
{
static void Run(object some_data)
{
int m = (int) some_data;
..
}
static void Main()
{
..
Thread thr = new Thread(Run);
thr.Start(some_data);
}
}
Дождаться завершения работы потоков можно с помощью метода Join:
thr1.Join(); thr2.Join();
В функции потока необходимо предусмотреть возможность разбиения диапазона 0.. (N-1) на число потоков nThr. При запуске потока в качестве аргумента передается либо "индекс потока", определяющий область массива, который обрабатывается в данном потоке, либо начальный и конечный индексы массива.
Многопоточное выполнение будет параллельным при наличии в вычислительной системе нескольких процессоров (ядер процессора). Число процессоров можно узнать с помощью свойства:
System.Environment.ProccessorCount;
Параллельное выполнение вычислений также можно реализовать с помощью классов библиотеки TPL (Task Parallel Library). Классы библиотеки располагаются в пространстве имен System.Threading.Tasks. Параллельное вычисление операций над элементами цикла выполняется с помощью метода Parallel.For:
Parallel.For(0, a.Length, i =>
{ b[i] = Math.Pow(a[i], 1.789); });
Для анализа производительности последовательного и параллельного выполнения можно использовать переменные типа DateTime. Например,
DateTime dt1, dt2;
dt1 = DateTime.Now;
// Вызов_вычислительной_процедуры;
dt2 = DateTime.Now;
TimeSpan ts = dt2 – dt1;
Console.WriteLine("Total time: {0}", ts.TotalMilliseconds);
Также можно использовать объект Stopwatch пространства System.Diagnostics:
Stopwatch sw = new Stopwatch();
sw.Start();
// Вызов_вычислительной_процедуры;
sw.Stop();
TimeSpan ts = sw.Elapsed;
Console.WriteLine("Total time: {0}", ts.TotalMilliseconds);
При оценке производительности необходимо учесть, что время выполнения алгоритма зависит от множества параметров. Поэтому желательно оценивать среднее время выполнения при нескольких прогонах алгоритма, исключая первый разогревающий прогон.
Эффективность параллельного алгоритма существенно зависит от элементов массива, числа потоков, сложности математической функции и т.д. Следует учитывать, что при малом объеме элементов массива, накладные расходы, связанные с организацией многопоточной обработки, превышают выигрыш от параллельности обработки. При последовательном выполнении примитивной циклической обработки быстродействие достигается за счет оптимального использования кэш-памяти.
Выполняя анализ зависимости быстродействия от числа потоков, следует учитывать число ядер процессора. Увеличение числа потоков сверх возможностей вычислительной системы приводит к конкуренции потоков и ухудшению быстродействия.
Усложнение обработки элементов массива предлагается реализовать с помощью внутреннего цикла. Например,
for(int i=0; i<a.Length; i++)
{
// Обработка i-элемента
for(int j=0; j < K; j++)
b[i] += Math.Pow(a[i], 1.789);
}
K – параметр "сложности". Увеличивая параметр K, наблюдаем повышение эффективности параллельной обработки при меньшем объеме массива чисел.
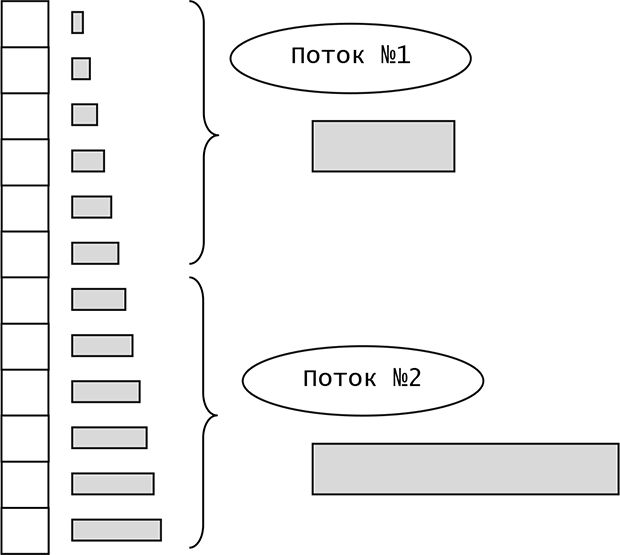
В рассмотренных вариантах обработки вычислительная нагрузка на каждой итерации относительно одинакова. В ситуациях, когда вычислительная нагрузка зависит от индекса элемента, разделение массива по равным диапазонам может быть не эффективно. Рассмотрим следующий вариант обработки:
for(int i=0; i<a.Length; i++)
{
// Обработка i-элемента
for(int j=0; j <i; j++)
b[i] += Math.Pow(a[i], 1.789);
}
Вычислительная нагрузка при обработке i-элемента зависит от индекса i. Обработка начальных элементов массива занимает меньшее время по сравнению с обработкой последних элементов. Разделение данных по диапазону приводит к несбалансированной загрузке потоков и снижению эффективности распараллеливания.
Одним из подходов к выравниванию загрузки потоков является применение круговой декомпозиции. В случае двух потоков получаем такую схему: первый поток обрабатывает все четные элементы, второй поток обрабатывает все нечетные элементы. Реализуйте круговую декомпозицию для нескольких потоков (больше двух).
Вопросы:
- Почему эффект от распараллеливания наблюдается только при большем числе элементов?
- Почему увеличение сложности обработки повышает эффективность многопоточной обработки?
- Какое число потоков является оптимальным для конкретной вычислительной системы?
- Почему неравномерность загрузки потоков приводит к снижению эффективности многопоточной обработки?
- Какие другие варианты декомпозиции позволяют увеличить равномерность загрузки потоков?
- В какой ситуации круговая декомпозиция не обеспечивает равномерную загрузку потоков?