Элементы математической статистики
5.3. Построение функции распределения и плотности распределения
Нормальное распределение
Функция плотности нормального распределения вероятности случайной величины имеет вид
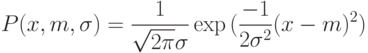 |
( 5.3) |
 - среднеквадратичное отклонение. Тогда функция нормального распределения будет:
- среднеквадратичное отклонение. Тогда функция нормального распределения будет:
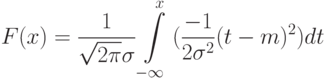 |
( 5.4) |
Пример 5.3
Для СВ, распределенной по нормальному закону построим функцию распределения вероятности , функцию плотности распределения вероятности и графики.
В MathCAD функции распределения находятся в категории Probaility distribution, функции плотности распределения находятся в категории Probability density. Используем функцию pnorm() и dnorm().
Функция 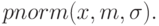 – рассчитывает в точке x значение функции распределения вероятности для нормального закона со средним m и среднеквадратичным отклонением
– рассчитывает в точке x значение функции распределения вероятности для нормального закона со средним m и среднеквадратичным отклонением  .
.
Функция 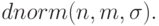 – рассчитывает в точке x значение функции плотности распределения вероятности для нормального закона со средним m и среднеквадратичным отклонением
– рассчитывает в точке x значение функции плотности распределения вероятности для нормального закона со средним m и среднеквадратичным отклонением  .
.
На листинге (Рис.5.3, Рис.5.4) созданы два вектора СВ с нормальным распределением и разными параметрами m и  : NR и NR1. В векторе NR (и NR1) каждое число имеет нормальное распределение с средним m и среднеквадратичным отклонением
: NR и NR1. В векторе NR (и NR1) каждое число имеет нормальное распределение с средним m и среднеквадратичным отклонением  .
.
Построены две функции распределения: FN(x) - для 1 элемента вектора 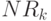 и FN1(x) - для 1 элемента вектора
и FN1(x) - для 1 элемента вектора 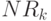 . Показаны график функций распределения FN(x) и FN1(x).
. Показаны график функций распределения FN(x) и FN1(x).
 ,
, 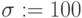
 ,
, 
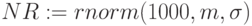 ,
, 
![FN(x):=pnorm[NR_1(x),m,\sigma]](/sites/default/files/tex_cache/2fd29c59cc3e3be2b426240b7e9cd733.png) ,
, ![FN1(x):=pnorm[NR1_1(x),m,\sigma]](/sites/default/files/tex_cache/96df64b5c227a2874f6dc125726e7492.png)
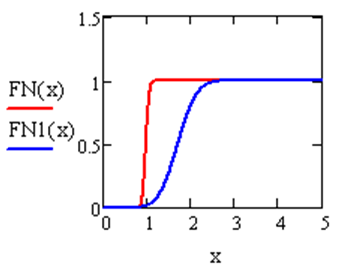
Рис. 5.3. Листинг решения примера 5.3. Функции распределения FN(x) и FN1(x) для нормального закона и их графики
![DN(x):=dnorm[NR_1(x),m,\sigma]](/sites/default/files/tex_cache/5e8b13a05eff7b755d6d473167ea877a.png) ,
, ![DN1(x):=pnorm[NR1_1(x),m,\sigma]](/sites/default/files/tex_cache/7d2d20d7f4fabbaf9a763fdcf7e3e351.png)
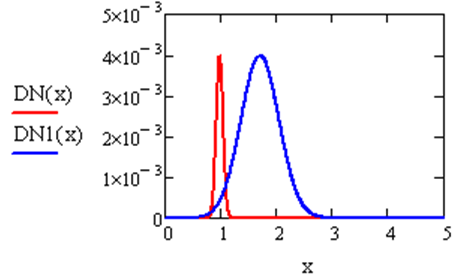
Рис. 5.4. Листинг решения примера 5.3. Функции плотности распределения DN(x) и DN1(x) для нормального закона и их графики
5.4. Построение гистограммы распределения случайной величины
Гистограммой называется график, аппроксимирующий по случайным данным плотность их распределения. При построении гистограммы область значений случайной величины (а,b) разбивается на некоторое количество n сегментов, а затем подсчитывается процент попадания данных в каждый сегмент. Для построения гистограмм в MathCAD имеется несколько встроенных функций. Рассмотрим две функции
Функция hist (int, x) – возвращает вектор частоты попадания случайной величины х в интервалы, определяемые вектором сегментов int на отрезке (a.b), сегменты находятся в порядке возрастания a<int<b.
Функция - histogram (bin, х) – возвращает двумерную матрицу на отрезке (a.b), 1 столбец которой содержит середины разбиения отрезка на bin сегментов , 2 столбец - вектор частоты попадания случайной величины х.
На примере экспоненциального распределения случайной величины с параметром 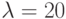 продемонстрируем технологию построения гистограммы распределения.
продемонстрируем технологию построения гистограммы распределения.
Экспоненциальное или показательное распределение
Непрерывная случайная величина х, принимающая неотрицательные значения в полубесконечном интервале 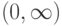 , имеет экспоненциальное распределение, если плотность распределения имеет вид:
, имеет экспоненциальное распределение, если плотность распределения имеет вид:
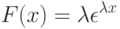 |
( 5.5) |
Функция распределения в этом случае имеет вид:
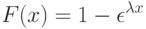 |
( 5.6) |
где 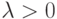 — положительная постоянная, параметр экспоненциального распределения.
— положительная постоянная, параметр экспоненциального распределения.
Числовые характеристики экспоненциального распределения определяются по следующим формулам:
Математическое ожидание  дисперсия
дисперсия  , среднеквадратичное отклонение
, среднеквадратичное отклонение 
Пример 5.4
Построим гистограмму распределения для случайной величины с экспоненциальным распределением. Рассмотрим два способа построения.
1 способ. Гистограмма с произвольными сегментами разбиения
Сначала генерируем совокупность СВ, распределенных по экспоненциальному закону с параметром 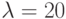 . С помощью функции
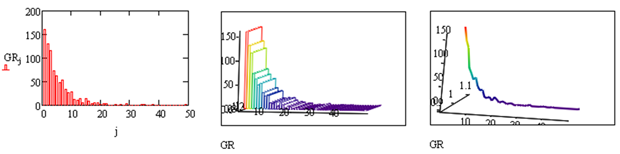
. С помощью функции 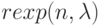 . построим массив R из n=1000 случайных величин. Область изменения R лежит в пределах от a=min(R) до b=max(R). Для построения гистограммы используем функцию hist (int, x) для 50 интервалов int=50. Листинг расчета, где получены вектор частоты попадания данных в интервалы гистограммы GR и вектор сегментов int, показан на pис.5.5. MathCAD создает GR и int в виде векторов и представляет в виде таблиц, где 1 столбец номер элементов, 2 столбец значения GR и int, соответственно. Графики построены на плоскости для индексной переменной и в виде для матрицы в де гистограммы и пространственной кривой.
. построим массив R из n=1000 случайных величин. Область изменения R лежит в пределах от a=min(R) до b=max(R). Для построения гистограммы используем функцию hist (int, x) для 50 интервалов int=50. Листинг расчета, где получены вектор частоты попадания данных в интервалы гистограммы GR и вектор сегментов int, показан на pис.5.5. MathCAD создает GR и int в виде векторов и представляет в виде таблиц, где 1 столбец номер элементов, 2 столбец значения GR и int, соответственно. Графики построены на плоскости для индексной переменной и в виде для матрицы в де гистограммы и пространственной кривой.

 ,
, 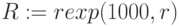

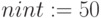
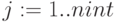
 ,
, 
 ,
, 
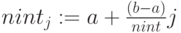 ,
, 

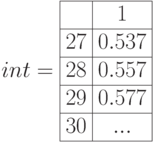
увеличить изображение
Рис. 5.5. Листинг решения примера 5.4. 1 способ построения гистограммы. Матрица гистограммы GR, матрица интервалов int. Гистграмма на плоскости и в трехмерном пространстве.
2 способ. Построение матрицы гистограммы
Для построения гистограммы массива R из 1000 СВ используем функцию histogram(bin, х). Область изменения R [a, b] также разобьем на 50 интервалов. MathCAD создает двумерную матрицу GR1, 1 столбец которой содержит середины разбиения отрезка (a, b) на bin=50 сегментов, 2 столбец - вектор частоты попадания случайной величины R. Рис.5.6 представляет матрицу гистограммы GR1 и ее графики. На плоскости график от индексной переменной: - по оси OX первый столбец матрицы, по оси OY – второй столбец матрицы. В пространстве график от матрицы в виде гистограммы и поверхности.
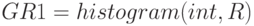

увеличить изображение
Рис. 5.6. Листинг решения примера 5.4. 2 способ построения гистограммы. Матрица гистограммы GR1. Гистграммы на плоскости и в трехмерном пространстве
Основные итоги
В лекции представлены методы работы со случайными величинами. Рассмотрены функции всех категорий: Random numbers, pnorm. dnorm  ;). Statistics. Probaility distribution, Probability density, с помощью которых можно генерировать случайные последовательности с заданным распределением, рассчитывать вероятности, находить статистические характеристики, строить гистограммы распределений. На примерах показано построение графиков случайных величин в виде одномерной функции индексной переменной и в виде совокупности точек поверхности.
;). Statistics. Probaility distribution, Probability density, с помощью которых можно генерировать случайные последовательности с заданным распределением, рассчитывать вероятности, находить статистические характеристики, строить гистограммы распределений. На примерах показано построение графиков случайных величин в виде одномерной функции индексной переменной и в виде совокупности точек поверхности.
Задания для самостоятельного выполнения
- Генерировать вектор из 5000 случайных чисел, распределенных по равномерному закону на отрезке [a,b]: a=5 b=40. Показать графическое представление точек случайной величины. Рассчитать статистические характеристики.
- Для сгенерированного вектора построить функцию распределения и плотность распределения. Показать графики и матрицы распределений.
- Построить гистограмму распределения для сгенерированной матрицы. Показать графики и матрицы.
- Сгенерировать последовательность из 1000 случайных чисел, распределенных по заданному закону. Построить гистограмму. Рассчитать характеристики распределения: математическое ожидание, дисперсию, среднеквадратичное отклонение, медиану.
Варианты законов распределения:
- Нормальный закон распределения , математическое ожидание 3, среднеквадратичное отклонение 1,5.
- Закон Пуассона, среднее 10.
- Логнормальный закон, среднее 5, отклонение 2.
- Гамма-распределение
 .
. - Нормальный закон распределения , матожидание 5, отклонение 1.
- Гамма-распределение (функция rgamma категории random numbers),
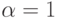 .
. - Закон Пуассона, среднее 3.
- Бета-распределение,
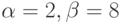
Ключевые термины
случайная величина - величина, которая в результате опыта может принять только одно из множества значений, до опыта, неизвестно, какое именно.
функция распределения – вероятность P для случайной величины X выполнения неравенства X < х, где х – одно их возможных значений СВ, F(x) = P( X < x ), F(x) - функция аргумента х.
плотность распределения вероятности – для непрерывной случайной величины X первая производная от функции распределения F(x):  .
.
Random number () – категория функций для генерации последовательности случайных величин.
Statistics () - категория функций для расчёта числовых характеристик случайных величин.
Probaility distribution - категория функций для построения распределения вероятности случайных величин.
Probability density - категория функций для построения распределения плотности вероятности случайных величин.
hist () – функция вычисления частотного распределения случайной величины для построения гистограммы с произвольными сегментами разбиения.
histogram() – функция вычисления частотного распределения случайной величины для построения гистограммы с разбиением на равные сегменты.