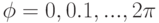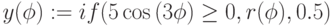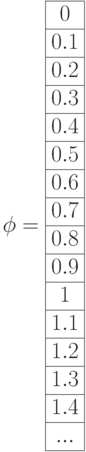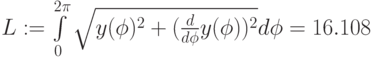Графика
3.2.3. Вычисление длины кривой
В декартовых координатах
Если кривая задана уравнением 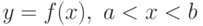 , то длина кривой
, то длина кривой 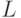 вычисляется
вычисляется
 |
( 3.1) |
Если кривая задана параметрически, 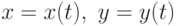 на интервале
на интервале 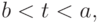 длина кривой L вычисляется
длина кривой L вычисляется
 |
( 3.2) |
В полярных координатах
 ,
, 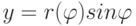 . Переменные x и y параметрические функции от
. Переменные x и y параметрические функции от  . Тогда длина кривой в полярных координатах имеет вид:
. Тогда длина кривой в полярных координатах имеет вид:
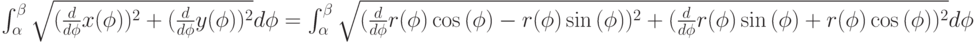
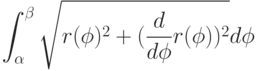 |
( 3.3) |
Пример 3.7
Вычислить длину кривой, заданной уравнением 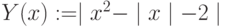 .
.
На Рис.3.13 показано вычисление длин участков кривой и всей кривой для x [-4;4]. Точки пересечения определяются с помощью трассировки. Длина кривой вычисляется по формуле (3.1.)

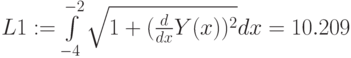
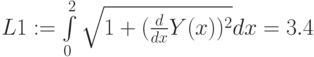
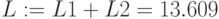
Пример 3.8
Построить график функции 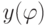 , заданной в виде:
, заданной в виде:
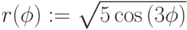 , если
, если 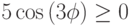
 , если
, если 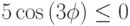
Вычислить длину кривой для ![\varphi [0, 2 \pi]](/sites/default/files/tex_cache/ebfe6fa726c9bf7b8cd0e0220aceffce.png) .
.
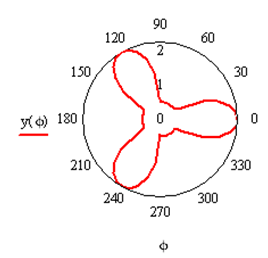
Функцию 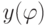 вводим, используя условную функцию. График строится в полярных координатах (Рис.3.18). В таблицах выведены значения аргумента – угла и функции. Длина кривой рассчитана по формуле (3.3).
вводим, используя условную функцию. График строится в полярных координатах (Рис.3.18). В таблицах выведены значения аргумента – угла и функции. Длина кривой рассчитана по формуле (3.3).
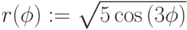 ,
,