Способы описания работы дискретных устройств
3.2 Граф-схемы алгоритмов
ГСА находят широкое применение в практике проектирования устройств ЦВМ и, в частности, микропрограммных автоматов в силу их хорошей обозримости, простоты конструкции языка и возможности преобразований и формального перехода к автоматному отображению.
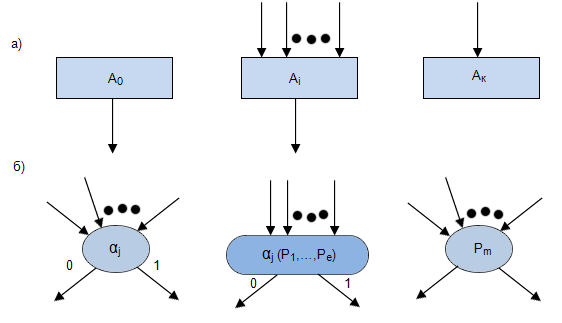
Основными символами, используемыми при записи граф-схем алгоритмов (ГСА), будем считать:
- операторы,
- логические условия,
- стрелки (рис.3.6).
Из всего множества операторов выделяются:
- начальный оператор
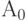 ,
, - конечный оператор
 ,
, - произвольный оператор
 .
.
Начальный оператор в дальнейшем (если это особо не оговаривается) будем рассматривать как оператор, символизирующий начало работы алгоритма.
Особенность записи оператора 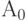 в ГСА состоит в том, что в этот оператор не входит ни одной стрелки.
в ГСА состоит в том, что в этот оператор не входит ни одной стрелки.
Конечный оператор будем рассматривать как оператор, символизирующий конец работы алгоритма.
Особенность записи оператора и  в ГСА состоит в том, что из этого оператора не выходит ни одной стрелки.
в ГСА состоит в том, что из этого оператора не выходит ни одной стрелки.
Произвольные операторы будем рассматривать как символы, обозначающие определённые действия, акты, связанные с реализацией алгоритма.
Особенность записи операторов 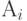 состоит в том, что в эти операторы могут входить несколько стрелок, но выходит всегда только одна стрелка.
состоит в том, что в эти операторы могут входить несколько стрелок, но выходит всегда только одна стрелка.
Под логическим условием будем понимать логическую функцию вида  , где
, где 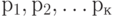 элементарные логические условия. Особенность записи логических условий состоит в том, что они могут иметь несколько входящих стрелок и только две выходящие, помеченные символами "О" и "I" в со-ответствии со значением логического условия. В дальнейшем будем допускать также ГСА замену левой части выражения вида
элементарные логические условия. Особенность записи логических условий состоит в том, что они могут иметь несколько входящих стрелок и только две выходящие, помеченные символами "О" и "I" в со-ответствии со значением логического условия. В дальнейшем будем допускать также ГСА замену левой части выражения вида 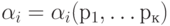 его правой частью.
его правой частью.
Стрелки обеспечивают упорядочение последовательности выполнения операторов и проверки логических условий, а также их взаимосвязей.
Выполнение алгоритма всегда начинается с оператора 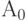 и заканчивается оператором
и заканчивается оператором  .
.
3.3Формулы переходов
В общем виде для каждой операторной вершины формула перехода записывается так:
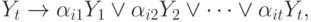
причем свойства ортогональности и полноты так же соблюдаются. Кроме того считается, что значения наборов логических условий в процессе выполнения операторов не меняются.
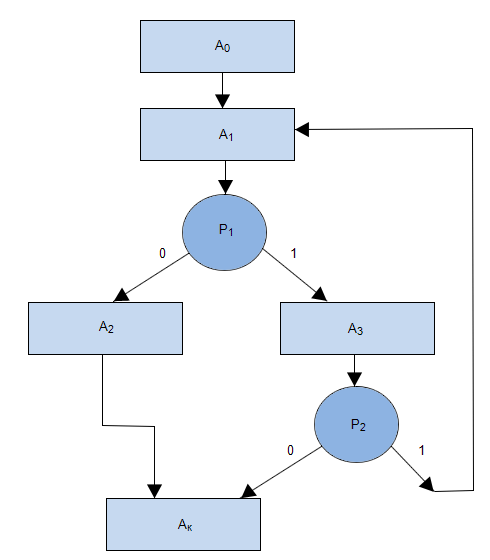
Для МП, представленной на рис.3.7, формулы перехода будут записаны так:
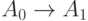 ;
;
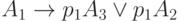 ;
;
 ;
;
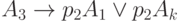 ;
;
3.4. Матричные схемы алгоритмов
Говорят, что задана матричная схема алгоритма (МСА), если задана матрица вида
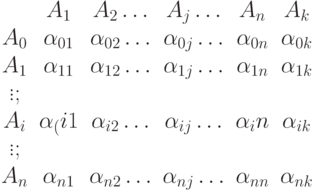
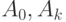 - начальный и конечный операторы,
- начальный и конечный операторы,
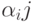 - логические условия, имеющие тот же смысл, что и в ГСА.
- логические условия, имеющие тот же смысл, что и в ГСА.
В MCA  принято рассматривать как такую логическую функцию, что если выполнялся оператор
принято рассматривать как такую логическую функцию, что если выполнялся оператор  и на образовавшемся наборе
и на образовавшемся наборе  значений элементарных логических условий функция
значений элементарных логических условий функция 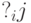 получила значение, равное единице, то непосредственно после оператора
получила значение, равное единице, то непосредственно после оператора  должен выполняться оператор
должен выполняться оператор 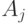 .
.

 -
-