|
Это в лекции 3. |
Эквивалентность формул и нормальные формы
Многочлены Жегалкина
Многочлены Жегалкина являются еще одним интересным подклассом формул, позволяющим однозначно представлять булевы функции.
Определение 4.4. Многочленами Жегалкина назваются формулы над множеством функций FJ={ 0, 1, *, +} (здесь * - это другое обозначение конъюнкции).
Таким образом, каждый многочлен Жегалкина (возможно, после раскрытия скобок и "приведения" подобных членов) представляет сумму (по модулю 2) положительных (монотонных) элементарных конъюнкций (т.е. элементарных конъюнкций без отрицаний). Поскольку для + и * справедливы законы ассоциативности, мы будем при записи многочлена Жегалкина опускать скобки, считая, что * связывает аргументы сильнее, чем +
Нетрудно проверить, что справедливы следующие эквивалентности:
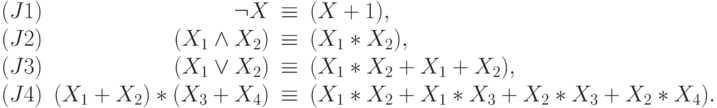
Из этих эквивалентностей и теоремы 4.1 легко получить первую часть следующего утверждения.
Теорема 4.3. Для любой булевой функции существует задающий ее многочлен Жегалкина. Он единственен с точностью до перестановок слагаемых и порядка переменных в конъюнкциях.
Доказательство Существование такого многочлена следует из того,
что для любой ДНФ или КНФ можно с помощью указанных эквивалентностей
найти эквивалентный многочлен Жегалкина: (J1)-(J3) позволяют заменять все
вхождения 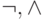 и
и  на + и *, а (J4) - перемножать получившиеся после такой замены многочлены.
на + и *, а (J4) - перемножать получившиеся после такой замены многочлены.
Для доказательства единственности представления подсчитаем
число различных многочленов Жегалкина от  переменных.
Каждая положительная элементарная конъюнкция имеет вид Xi1 * ... * Xik
,
где 1 <= i1 < ... < ik <= n
.
Таких конъюнкций столько же, сколько подмножеств множества
переменных.
Каждая положительная элементарная конъюнкция имеет вид Xi1 * ... * Xik
,
где 1 <= i1 < ... < ik <= n
.
Таких конъюнкций столько же, сколько подмножеств множества 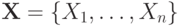 , т.е. 2n
.
(Конъюнкция, соответствующая пустому подмножеству переменных равна 1).
Упорядочим их произвольным образом (например, лексикографически):
, т.е. 2n
.
(Конъюнкция, соответствующая пустому подмножеству переменных равна 1).
Упорядочим их произвольным образом (например, лексикографически): 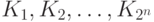 .
Tогда каждый многочлен Жегалкина единственным образом можно представить как сумму
.
Tогда каждый многочлен Жегалкина единственным образом можно представить как сумму
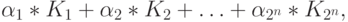
где каждый из коэффициентов 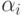 равен 0 или 1. Следовательно,
число многочленов Жегалкина равно
равен 0 или 1. Следовательно,
число многочленов Жегалкина равно 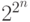 , т.е. числу всех булевых
функций от n переменных. Поэтому каждая функция задается в
точности одним многочленом Жегалкина.
, т.е. числу всех булевых
функций от n переменных. Поэтому каждая функция задается в
точности одним многочленом Жегалкина.
Пример 4.3. Пусть функция f(X1,X2,X3)
задается ДНФ 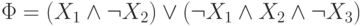 .
Найдем полином Жегалкина, который также задает эту функцию.
.
Найдем полином Жегалкина, который также задает эту функцию.
Сначала заменяем  на *, а затем,применяя
эквивалентность (J1), устраняем отрицания и получаем:
на *, а затем,применяя
эквивалентность (J1), устраняем отрицания и получаем:
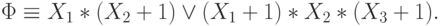
Перемножив по правилам (J4), получим:
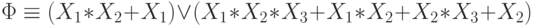
Эквивалентность (J3) позволяет устранить 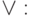
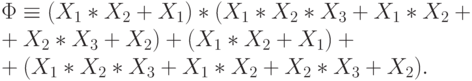
Снова, используя (J4), перемножим первые две скобки и устраним повторения переменных в конъюнкциях:
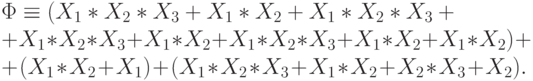
Упростим эту сумму, используя эквивалентности: 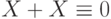 и
и 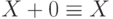 . В результате получим многочлен Жегалкина
. В результате получим многочлен Жегалкина
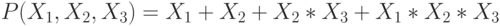
Если функция f(X1, ..., Xn)
задана таблично, то для построения реализующего ее многочлена Жегалкина можно применить метод
неопределенных коэфициентов. Сопоставим i -ому набору значений переменных 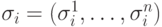 в таблице
положительную конъюнкцию
в таблице
положительную конъюнкцию 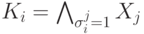 переменных, равных 1 в этом
наборе.
В частности, K1 - пустая конъюнкция, K2 = Xn,
K3 = Xn-1,
K4 = (Xn * Xn-1).
и т.д. Тогда для получения нужного многочлена Жегалкина достаточно
определить все коэффициенты
переменных, равных 1 в этом
наборе.
В частности, K1 - пустая конъюнкция, K2 = Xn,
K3 = Xn-1,
K4 = (Xn * Xn-1).
и т.д. Тогда для получения нужного многочлена Жегалкина достаточно
определить все коэффициенты 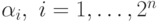 , в
выражении
, в
выражении
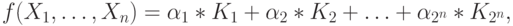
Подставляя в это равенство значения переменных из набора 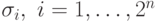 ,
мы получим 2n линейных уравнений относительно 2n
неизвестных коэффициентов
,
мы получим 2n линейных уравнений относительно 2n
неизвестных коэффициентов 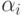 . Решив эту систему, получим требуемый многочлен
Жегалкина. Эта система треугольная и легко решается "сверху-вниз":
каждое
. Решив эту систему, получим требуемый многочлен
Жегалкина. Эта система треугольная и легко решается "сверху-вниз":
каждое 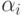 определяется по значениям
определяется по значениям  из уравнения, соответствующего
набору
из уравнения, соответствующего
набору 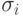 .
.
Пример 4.4. Рассмотрим в качестве примера функцию f(X1, ..., Xn), заданную следующей таблицей.
| X1 | X2 | X3 | f(X1, X2, X3) |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1. | 1 | 1 |
Многочлен Жегалкина для нее (как и для любой функции от 3-х переменных) представляется в виде
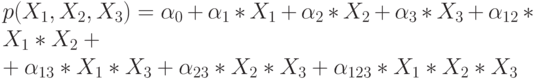
В этом представлении в индексах у коэффициентов  перечислены переменные, входящие в соответствующие конъюнкции.
перечислены переменные, входящие в соответствующие конъюнкции.
Последовательно подставляя значения переменных и f из таблицы, получаем:
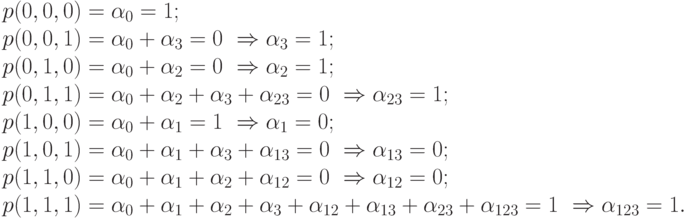
Следовательно, функция f(X1, X2, X3) представляется многочленом Жегалкина
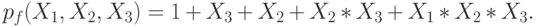
Задачи
Задача 4.1. Проверьте все приведенные в "лекции 4" эквивалентности (1) - (8), непосредственно вычисляя функции, представляемые их левыми и правыми частями.
Задача 4.2. Назовем логическим произведением формулу вида 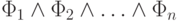 (в этом выражении
использованы соглашения о сокращении записи!). Ее подформулы
(в этом выражении
использованы соглашения о сокращении записи!). Ее подформулы 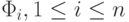 , , будем называть сомножителями.
Аналогично, логической суммой назовем формулу вида
, , будем называть сомножителями.
Аналогично, логической суммой назовем формулу вида 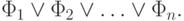 Ее подформулы
Ее подформулы 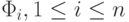 ,, будем называть слагаемыми.
,, будем называть слагаемыми.
Покажите, что из основных тождеств можно вывести следующие правила преобразования логических произведений и сумм.
- Если в логическом произведении один из сомножителей равен 0, то и все произведение равно 0.
- Если в логической сумме одно из слагаемых равно 1, то и вся сумма равна 1.
- Если в логическом произведении n >= 2 и есть сомножитель, равный 1, то его можно вычеркнуть.
- Если в логической сумме n >= 2 и есть слагаемое, равное 0, то его можно вычеркнуть.
Задача 4.3. Используя основные тождества, доказать эквивалентность следующих пар формул.
-
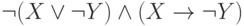 и
и 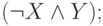
-
![\neg [(X \wedge \neg Y) \to (\neg X \vee Z)]](/sites/default/files/tex_cache/a59df306de81dde4fb084723a7783c86.png) и
и  ;
; -
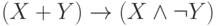 и
и 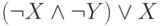 .
.
Задача 4.4. Докажите теорему 4.1, проверив, что
для любого набора значений аргументов 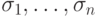 выполнены равенства
выполнены равенства 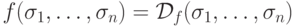 и
и 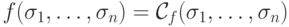 .
.
Задача 4.5.
- Предложите процедуру, которая по произвольной элементарной конъюнкции строит эквивалентную ей совершенную ДНФ.
- Предложите процедуру, которая по произвольной элементарной дизъюнкции строит эквивалентную ей совершенную КНФ.
Задача 4.6.
Докажите, что для любого k <= n каждую булеву функцию 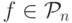 можно представить в виде
можно представить в виде
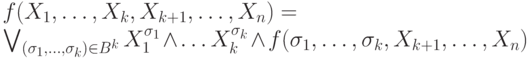
Такое представление называется разложением  по
по  .
При k=n из него получается совершенная ДНФ из теоремы
.
При k=n из него получается совершенная ДНФ из теоремы
Задача 4.7. Докажите предложение 4.1, используя индукцию по общему количеству функций  и + в формуле.
и + в формуле.
Задача 4.8. Как изменить (3)-ий, (4)-ый и (5)-ый этапы процедуры "Приведение к совершенной ДНФ ", чтобы в результате получить процедуру "Приведение к совершенной КНФ ", которая по произвольной формуле строит эквивалентную совершенную КНФ.
Задача 4.9. Найти эквивалентные сокращенные ДНФ и доказать эквивалентность следующих пар формул:
-
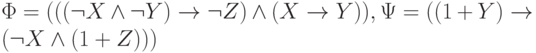 .
. -
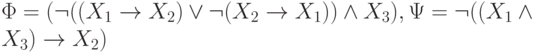 .
. -
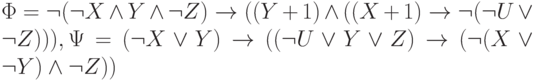 .
.
Задача 4.10. Используя основные эквивалентности, найти эквивалентные многочлены Жегалкина и доказать эквивалентность следующих формул:

Задача 4.11. Найти сокращенную дизъюнктивную нормальную форму и многочлен Жегалкина (методом неопределенных коэффициентов) для следующих функций от трех аргументов. Считаем, что наборы их аргументов упорядочены лексикографически и значения на них задаются последовательностью 8 нулей и единиц.
- f=(0010 1100)
- f=(1110 1100)
- f=(1100 0011)
- f=(0110 1011)

