|
Это в лекции 3. |
Индукция и комбинаторика
Принцип включения и исключения
Во многих ситуациях для подсчета числа объектов, обладающих тем или иным набором свойств, используется следующий принцип включения и исключения.
Пусть имеется N объектов, каждый из которых может обладать или не обладать
одним или несколькими свойствами p1,p2,... , pn. Через pi' будем обозначать
свойство, дополнительное к свойству pi, т.е. , если объект не обладает свойством pi, то он обладает свойством pi' . Через  при j=1,...,k, обозначим число объектов, обладающих свойствами q1,...,qk. Например, N(p1, p3', p4) - это число объектов, обладающих свойствами p1 и p4 и не обладающих
свойством p3.
при j=1,...,k, обозначим число объектов, обладающих свойствами q1,...,qk. Например, N(p1, p3', p4) - это число объектов, обладающих свойствами p1 и p4 и не обладающих
свойством p3.
Теорема 2.5. Число объектов, не обладающих ни одним из свойств p1,... , pn равно
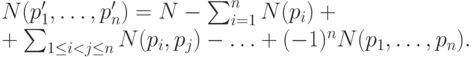
Доказательство проведем индукцией по числу свойств n.
Базис индукции. При n=1 очевидно, что N(p1') = N - N(p1).
Шаг индукции. Предположим, что для k свойств p1,p2,... , pk теорема справедлива, т.е.
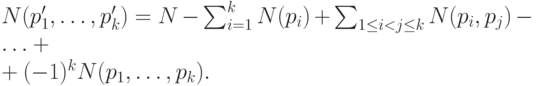
Применяя это соотношение ко множеству из N(pk+1) объектов, обладающих свойством pk+1, находим
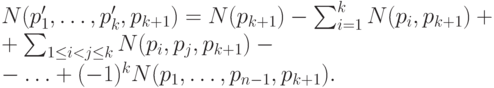
Вычитая последнее равенство из предыдущего, получаем утверждение теоремы при n=k+1 (заметим, что N(p1', ... , pk') - N(p1', ... , pk',p{k+1})=N(p1', ... , pk',pk+1') ).
В качестве примера рассмотрим следующую задачу.
Пример 2.2. В студенческой группе 25 студентов. Из них 15 знают язык Паскаль, 10 - язык Си и 14 - язык Бэйсик. Кроме того, 7 студентов знают Паскаль и Си, 10 студентов - Паскаль и Бэйсик, 8 студентов - Си и Бэйсик, а 5 студентов знают все три языка. Сколько студентов не знают ни одного из трех языков программирования?
Обозначив через p1 - свойство "знать Паскаль", через p2 - свойство "знать Си" и через p3 - свойство "знать Бэйсик", мы можем записать данные задачи следующим образом: N = 25, N(p1)=15, N(p2) = 10, N(p3)=14, N(p1,p2)=7, N(p1,p3)=10, N(p2,p3)=8, N(p1,p2,p3)=5. Тогда по формуле включения и исключения число студентов, не знающих ни одного языка программирования, равно N(p1',p2',p3')= 25 -(15 +10 +14) +(7+10+8)-5 = 6.
Задачи
Задача 2.6. Докажите формулу бинома Ньютона, используя метод математической индукции.
Задача 2.7. Доказать тождества:
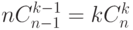
-
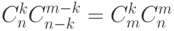 .
.
Задача 2.8. Доказать, что
![C_n^0 < C_n^1 < \ldots < C_n^{[n/2]} = C_n^{]n/2[} > C_n^{]n/2[+1}> \ldots > C_n^n](/sites/default/files/tex_cache/447150206e0cf63b99aee0fa1378c7e9.png)
Задача 2.9. Докажите, что число упорядоченных разбиений n -элементного множества на k подмножеств, первое из которых содержит n1 элементов, второе - n2 элементов,..., k -ое - nk элементов, равно
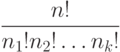
Задача 2.10. Преподаватель рассчитывает читать один и тот же курс в течение 20 лет. Чтобы не наскучить студентам, он решил рассказывать им каждый год 3 анекдота и не повторять никакие два года одни и те же три анекдота. Каково минимальное число анекдотов, которые он должен приготовить?
Задача 2.11. На острове N живет племя туземцев, у которых набор зубов во рту состоит из 30 зубов. При этом на острове нет двух жителей с одинаковыми наборами зубов. Может ли на острове N быть больше жителей чем в
а) Торжке? б) Твери? в) Москве? г) России? д) всем мире?
Задача 2.12. Доказать тождество Коши:
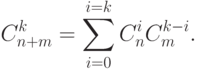
Указание: покажите, что обе части этого равенства задают количество вариантов выбора k человек из группы, состоящей из n женщин и m мужчин.
Задача 2.13. Докажите, что число способов, которыми можно породить k -элементное множество с повторениями, имея n разных элементов, например, 1, 2,..., n, из которых каждый может использоваться произвольное число раз, равно Cn+k-1k. (Например, при n=5, k=4 множество { 1,2,1,3} равно множеству {3,1,1,2} и не равно множеству {1, 2,2,3} ).
Задача 2.14. В кондитерском магазине продаются 4 сорта пирожных: заварные, песочные, "картошка" и бисквитные. Сколькими способами можно купить 6 пирожных?
Задача 2.15. Назовем два исхода первенства России по футболу совпадающими в главном, если в этих исходах совпадают обладатели золотых, серебренных и бронзовых медалей, а также две команды, покидающие премьер-лигу (т.е. занявшие два последних места). Найдите число различных в главном исходов (напомним, что в первенстве участвуют 16 команд).
Задача 2.16. За круглым столом короля Артура сидят 12 рыцарей. Каждый из них враждует со своими соседями. Нужно выбрать 5 рыцарей, чтобы освободить принцессу. Сколькими способами это можно сделать так, чтобы среди выбранных рыцарей не оказалось врагов?
Решите эту задачу в случае, когда из n рыцарей за столом нужно выбрать k рыцарей.
Задача 2.17. Установите принцип включения и исключения в теоретико-множественной форме. Пусть A1,..., An - это подмножества некоторого конечного множества X. Тогда
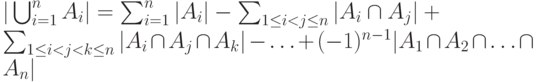
Задача 2.18. Сколько чисел в первой сотне не делится ни на одно из чисел 2, 3, 5? А в первой тысяче чисел?
Задача 2.19. Сколько целочисленных решений имеет система:

Задача 2.20. Найти число перестановок из n -элементов, при которых ни один элемент не остается в первоначальном положении.
