| Россия |
Вычислимые функции, тезис Тьюринга-Черча и неразрешимые проблемы
В этом лекции мы установим, что классы частично рекурсивных функций, функций, вычислимых структурированными программами, и функций, вычислимых машинами Тьюринга, совпадают. Это (вместе с эквивалентностью этого класса многим другим определениям вычислимости, не рассматриваемым в этих лекциях) позволяет считать этот класс функций точно отражающим наши интуитивные представления о вычислимости.
Напомним, что в теореме 8.1 мы уже показали, что каждая ч.р.ф. вычислима некоторой структурированной программой.
Вычислимость частично рекурсивных функций по Тьюрингу
Теорема 10.1. Для всякой ч.р.ф. f существует
м.Т. 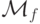 , вычисляющая функцию f.
, вычисляющая функцию f.
Доказательство. Доказательство проведем индукцией по определению частично рекурсивной функции f.
Базис. Вычислимость простейших функций машинами Тьюринга очевидна.
Индукционный шаг. Покажем, что операторы суперпозиции, примитивной рекурсии и минимизации сохраняют вычислимость по Тьюрингу. Все используемые м.Т. будем предполагать односторонними со стандартными заключительными конфигурациями.
Суперпозиция. Пусть Fm и fn1,..., fnm
- ч.р.ф., вычислимые на м.Т. 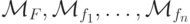 , соответственно. Пусть функция Gn
получена из них с помощью суперпозиции: Gn=[Fm;fn1,..., fnm]. Тогда м.Т.
, соответственно. Пусть функция Gn
получена из них с помощью суперпозиции: Gn=[Fm;fn1,..., fnm]. Тогда м.Т. 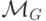 ,
вычисляющая G, работает следующим образом:
,
вычисляющая G, работает следующим образом:
-
m раз копирует вход
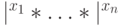 , отделяя одну копию от другой символом # ;
, отделяя одну копию от другой символом # ; - на полученном слове вида
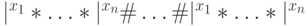
- запускает параллельную композицию машин
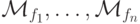 и получает конфигурацию вида
и получает конфигурацию вида  , где
, где ![y_{i}=f_{i}(x_{1},\dots ,x_{n}) (i \in [1,m])](/sites/default/files/tex_cache/e25e0e3aed1c51c073d6cc632d81e8de.png) .
. - заменяет все символы 0023 на * ;
- затем запускает программу м.Т.
 на получившемся после этапа 3) входе вида
на получившемся после этапа 3) входе вида  , и вычисляет требуемое значение
, и вычисляет требуемое значение 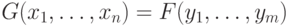 .
.
Если обозначить м.Т., выполняющую копирование на этапе (1), через Копm,
а м.Т., выполняющую замену # на * на этапе (3), через Зам*#, то требуемую для суперпозиции м.Т. 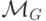 можно представить как
можно представить как
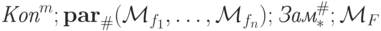
Примитивная рекурсия. Пусть функция Fn+1(x1,... ,xn,y) получена с помощью оператора
примитивной рекурсии из функций gn(x1,..., xn) и fn+2(x1,... ,xn, y, z), которые вычислимы на м.Т. 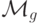 и
и 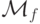 . Определим вспомогательные м.Т.:
. Определим вспомогательные м.Т.:
-
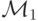 , используя
, используя 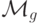 , строит по входу вида
, строит по входу вида  конфигурацию на ленте
конфигурацию на ленте 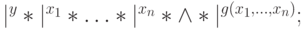
-
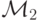 , используя
, используя 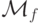 , строит по входу вида
, строит по входу вида  конфигурацию
конфигурацию 
-
 на входе вида
на входе вида  выдает в качестве результата
выдает в качестве результата 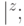
-
 на входе вида
на входе вида  проверяет условие
проверяет условие 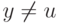 .
.
Построение каждой из указанных м.Т. достаточно очевидно.
Из них можно получить, используя определенные в предыдущем
разделе конструкции
"языка программирования" для машин Тьюринга, требуемую м.Т.  :
:

Минимизация. Пусть ![f^{n}(x_{1},\dots , x_{n}) = \mu y [ g^{n+1}(x_{1},\dots , x_{n},y)=0]](/sites/default/files/tex_cache/741e1f062158385930c740d23e2e43f1.png) и м.Т.
и м.Т. 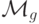 вычисляет функцию gn+1.
Определим следующие вспомогательные м.Т.:
вычисляет функцию gn+1.
Определим следующие вспомогательные м.Т.:
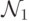 приписывает аргумент 0 ко входу, т.е. вход вида
приписывает аргумент 0 ко входу, т.е. вход вида 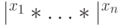 переводит в конфигурацию на ленте
переводит в конфигурацию на ленте  (напомним, что при унарном кодировании 0 соответствует пустой символ).
(напомним, что при унарном кодировании 0 соответствует пустой символ).
 копирует свой вход с разделителем #, т.е. по любому входу w выдает w # w.
копирует свой вход с разделителем #, т.е. по любому входу w выдает w # w.
Через E обозначим м.Т., которая ничего не делает.
Пусть  , т.е. вход вида
, т.е. вход вида 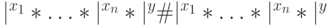 машина
машина  перерабатывает, используя
перерабатывает, используя 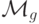 ,
в
,
в  , где z= g(x1,... ,xn, y)
, где z= g(x1,... ,xn, y)
 на входе вида w # v проверяет непустоту v (т.е. условие v > 0 ).
на входе вида w # v проверяет непустоту v (т.е. условие v > 0 ).
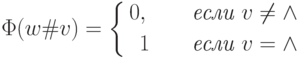
Таким образом, при v=g(x1,...,xn,y) машина  проверяет
условие
проверяет
условие 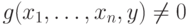 .
.
 по входу вида
по входу вида  стирает #w и прибавляет
к y единицу, т.е. выдает результат:
стирает #w и прибавляет
к y единицу, т.е. выдает результат:  .
.
Наконец, 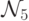 по входу
по входу  выдает |y, стирая ненужные блоки символов.
выдает |y, стирая ненужные блоки символов.
Ясно, что каждая из перечисленных м.Т.  ,
,  ,
,  ,
,  ,
,  и
и  легко реализуема. Построим теперь с их помощью
следующую м.Т.
легко реализуема. Построим теперь с их помощью
следующую м.Т. 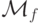 :
:
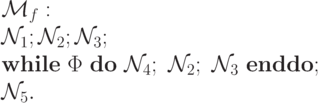
Из этого определения непосредственно следует, что  вычисляет функцию fn(x1,..., xn),
заданную с помощью оператора минимизации.
вычисляет функцию fn(x1,..., xn),
заданную с помощью оператора минимизации.
