НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 8: Численное интегрирование

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 25.10.2007 | Уровень: специалист | Доступ: свободно | ВУЗ: Московский физико-технический институт

Вам нравится? Нравится 54 студентам

| Поделиться |

Поддержать программу

7.8. Задачи для самостоятельного решения

Предложить алгоритмы вычисления интегралов от быстро осциллирующих функций:
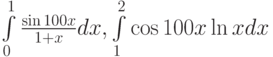
$\int\limits_0^1 {\frac{\sin 100x}{1 + x}dx}, \int\limits_1^2\cos 100 x\ln xdx}$

(формулы Филона. Подробнее о них в [7.3]).
Предложить алгоритм вычисления интегралов:
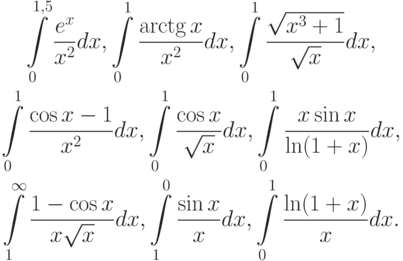
$\begin{gather*} \int\limits_0^{1, 5}{\frac{e^{x}}{x^2 }dx}, \int\limits_0^1 {\frac{\arctg x}{x^2 }dx}, \int\limits_0^1 {\frac{\sqrt{x^3 + 1}}{\sqrt {x}}dx}, \\ \int\limits_0^1 {\frac{\cos x - 1}{x^2 }dx}, \int\limits_0^1 {\frac{\cos x}{\sqrt{x}}dx}, \int\limits_0^1 {\frac{x\sin x}{\ln (1 + x)}dx}, \\ \int\limits_1^\infty {\frac{1 - \cos x}{x\sqrt {x}}dx, }\int\limits_1^0 {\frac{\sin x}{x}dx}, \int\limits_0^1 {\frac{\ln (1 + x)}{x}dx} . \end{gather*}$
Доказать, что формула Симпсона точна, если подынтегральная функция есть произвольный многочлен третьей степени.
Определить число $\pi$ по формуле
$\pi = \int\limits_0^1 {\frac{4}{1 + x^2 }dx, }$

используя формулы прямоугольников с центральной точкой, трапеций, Симпсона.
Оценить число разбиений отрезка для вычисления интеграла
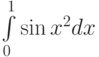
$\int\limits_0^1 {\sin x^2 dx}$

по формуле прямоугольников с центральной точкой для достижения точности $\varepsilon = 10^{ - 4}.$ Тот же вопрос для подсчета интеграла

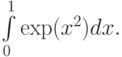
$\int\limits_0^1 {\exp (x^2 )} dx.$
Оценить погрешность при вычислении интеграла
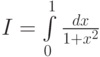
$I = \int\limits_0^1 {\frac{dx}{1 + x^2 }}$

по формуле прямоугольников с центральной точкой, трапеций, Симпсона.
На элементарном отрезке [x_i, x_{i - 1}] подынтегральная функция аппроксимируется кубическим сплайном:
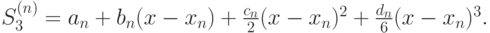
$S_3^{(n)} = a_n + b_n (x - x_n) + \frac{c_n}{2}(x - x_n)^2 + \frac{d_n}{6}(x - x_n)^3 .$

Вывести соответствующую формулу сплайн - квадратуры и исследовать ее точность.