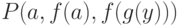Логическое программирование

Элементы языка Пролог

Основным элементом языка Пролог является терм. Термы строятся из переменных, атомов, чисел и функторов с использованием круглых скобок.

Переменная — это цепочка (слово), составленная из букв, цифр и символа подчеркивания, начинающаяся с большой буквы или символа подчеркивания. Если переменная используется однажды, то вместо нее можно использовать так называемую анонимную переменную, состоящую из одного символа подчеркивания.

Атом — это цепочка, составленная из букв, цифр и символа подчеркивания, начинающаяся с маленькой буквы или с большой буквы, но тогда в одинарных кавычках. Последний способ удобен, если атом является собственным именем. Иногда атомы строятся и из специальных знаков, но мы не будем их использовать при первоначальном знакомстве.

Числа записываются традиционным образом. Числа с плавающей запятой в обычных применениях Пролога используются редко из-за ошибок округления.

Функтор синтаксически совпадает с атомом.

Терм — это либо переменная, либо атом, либо число, либо выражение вида

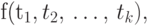
где — функтор, а 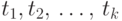— термы.

Для некоторых специальных функторов, например знаков арифметических операций, отношений сравнения и других, в Прологе, как в традиционной математике, используется инфиксная форма записи. Например, выражение 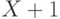рассматривается как терм с функтором 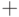и двумя аргументами и .

Среди термов ввиду особой важности выделяются термы для представления списков. Канонически список представляется двухместным термом, первым аргументом которого является головной элемент списка, а вторым — его хвост, то есть список, полученный из исходного удалением головного элемента. Функтором в такой записи часто используется символ точка. Альтернативным представлением списка является выражение вида или , где — головной элемент, а — хвост списка. Допустимо также выражение вида .

Важным инструментом в языке Пролог является унификация термов с помощью подстановок. Такую унификацию мы применяли выше в примерах на доказательство методом резолюций. Сейчас более подробно рассмотрим понятие унификации.

Подстановкой называется набор пар 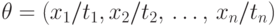, где — переменные, а 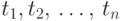— термы.

Через обозначим результат подстановки термов 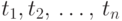в выражение вместо переменных .

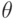Пусть — еще одна подстановка. Композиция двух подстановок и определяется следующим образом:

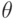Подстановка может быть вычислена следующим образом. Составим из подстановок и последовательность и проведем следующие две операции:

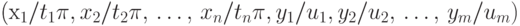
1. Если некоторое совпадает с некоторым , то вычеркиваем пару .
2. Если , то вычеркиваем пару .

Пример. Пусть 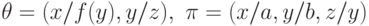. Рассмотрим последовательность

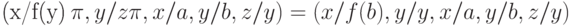
и по первому правилу вычеркиваем пары и 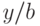, затем по второму правилу — пару 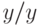. В результате получим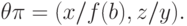

Подстановка 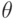называется унификатором термов , , если .

Наиболее общим унификатором термов , называется подстановка , такая, что любой другой их унификатор 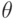представляется в виде .

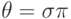Пример. Для термов 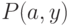, 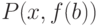унификатором будет подстановка

Будет ли она наиболее общим унификатором?

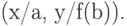
Пример.

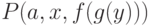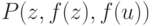Для термов и наиболее общим унификатором будет подстановка 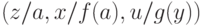. Результатом унификации будет терм