|
на стр 6, лекции 3, Очевидно "Ck <= модуль(Gk(е))*b(k+1)" (1) - , подскажите что значит "модуль" и почему это очевидно... |
Поисковые деревья
Упражнения
- Предположим, что корень красно-черного дерева красный. Если мы покрасим его в черный цвет, останется ли дерево красно-черным?
- Покажите, что самый длинный путь вниз от вершины
 к листу не
более чем вдвое длиннее самого короткого такого пути.
к листу не
более чем вдвое длиннее самого короткого такого пути. - Какое наибольшее и наименьшее количество внутренних узлов может быть
в красно-черном дереве черной высоты
Вращения — это манипуляции
с красно-черными деревьями с целью
восстановления RB-свойств в случае их нарушения. Их используют при
реализации операций  и
и  .
Вращение представляет собой локальную операцию, при которой меняется несколько указателей,
но свойство упорядоченности сохраняется.
.
Вращение представляет собой локальную операцию, при которой меняется несколько указателей,
но свойство упорядоченности сохраняется.
На рис. 10.1 показаны два взаимно обратных вращения: левое и правое.
Левое вращение возможно в
любом узле  , правый ребенок
которого (назовем его
, правый ребенок
которого (назовем его  ) не является листом (
) не является листом (  ). После вращения
). После вращения  оказывается корнем
поддерева,
оказывается корнем
поддерева,  — левым ребенком
узла
— левым ребенком
узла  , а бывший левый ребенок
, а бывший левый ребенок  — правым
ребенком узла
— правым
ребенком узла  .
.
Упражнения
- Покажите, что левое и правое вращения можно
осуществить за время
 .
. - Напишите процедуры
 и
и  , реализующие левое и правое вращение
в дереве
, реализующие левое и правое вращение
в дереве  относительно узла
относительно узла  .
. - Пусть
 ,
,  и
и  — произвольные
узлы в поддеревьях
— произвольные
узлы в поддеревьях  ,
,  и
и  на
рис. 10.1 (справа).
Как изменится глубина
на
рис. 10.1 (справа).
Как изменится глубина  ,
,  и
и  при
выполнении левого вращения?
при
выполнении левого вращения? - Покажите, что произвольное двоичное дерево поиска с
 узлами
может быть преобразовано в любое другое дерево с тем же числом узлов
(и теми же ключами) с помощью
узлами
может быть преобразовано в любое другое дерево с тем же числом узлов
(и теми же ключами) с помощью  вращений. (Указание: сначала
покажите, что
вращений. (Указание: сначала
покажите, что 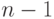 правых вращений достаточно, чтобы преобразовать
любое дерево в идущую вправо цепочку.)
правых вращений достаточно, чтобы преобразовать
любое дерево в идущую вправо цепочку.) - Напишите процедуры Insert ( T, x ) и Delete ( T, x ), которые добавляют и удаляют элемент x из дерева T за время
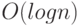 .
. - Разработайте алгоритм объединения двух красно-черных деревьев в одно
красно-черное дерево за время
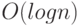 .
.
АВЛ-деревья
АВЛ-балансировка по определению требует, чтобы для каждого узла высота его правого поддерева отличалась от высоты левого не более чем на единицу.
Пусть 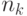 — минимальное число узлов в АВЛ-дереве
высоты
— минимальное число узлов в АВЛ-дереве
высоты  .
Тогда
.
Тогда  ,
, 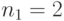 ,
,  ,
, 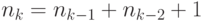 при
при 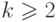 .
.
Теорема.
Для любого 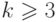 выполняется неравенство
выполняется неравенство 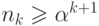 ,
где
,
где  — положительный корень
уравнения
— положительный корень
уравнения 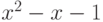 .
.
Доказательство.
Непосредственно проверяется базис индукции 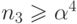 ,
, 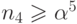 . Предположим теперь, что при
. Предположим теперь, что при 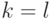 выполняется неравенство
выполняется неравенство 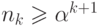 ,
и докажем его при
,
и докажем его при 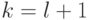 .
Действительно,
.
Действительно, 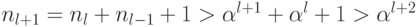 . Докажем последнее в этой цепочке
неравенство.
. Докажем последнее в этой цепочке
неравенство.
Пусть 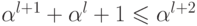 ,
тогда
,
тогда  и, следовательно,
и, следовательно, 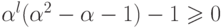 .
Получили противоречие
.
Получили противоречие 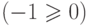 .
.
Следствие.
Для любого АВЛ-дерева высоты  с
с  узлами
выполняется соотношение
узлами
выполняется соотношение 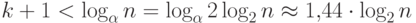 , что обеспечивает "логарифмическую
трудоемкость" выполнения основных операций с АВЛ-деревом.
, что обеспечивает "логарифмическую
трудоемкость" выполнения основных операций с АВЛ-деревом.
Идея балансировки двоичных деревьев поиска принадлежит\linebreak
Г.М.Адельсону-Вельскому и Е.М.Ландису, предложившим в 1962 г. класс
сбалансированных деревьев, называемых с тех пор АВЛ-деревьями. Баланс
поддерживается с помощью процедуры вращения. Для его восстановления
в дереве с  узлами после добавления или удаления узла может
потребоваться
узлами после добавления или удаления узла может
потребоваться  вращений.
вращений.
Еще один класс деревьев поиска,
называемых  -
-  -деревьями, был предложен
Дж. Хопкрофтом в 1970 г. Здесь баланс поддерживается за счет изменения
степеней узлов. Обобщение
-деревьями, был предложен
Дж. Хопкрофтом в 1970 г. Здесь баланс поддерживается за счет изменения
степеней узлов. Обобщение  -
-  -деревьев предложили
Д.Байер и Е.Мак-Крейт.
Их деревья называются Б-деревьями, которые мы рассмотрим в следующем разделе.
-деревьев предложили
Д.Байер и Е.Мак-Крейт.
Их деревья называются Б-деревьями, которые мы рассмотрим в следующем разделе.
Красно-черные деревья предложил Д.Байер, назвав их симметричными двоичными Б-деревьями. Л.Гибас подробно изучил их свойства и предложил использовать для наглядности красный и черный цвета Посмотрите [7].
Из многих других вариаций на тему сбалансированных деревьев наиболее
интересны расширяющиеся деревья, которые придумали Д.Слеатор и Р.Тарьян.
Эти деревья являются саморегулирующимися. Хорошее описание расширяющихся
деревьев дал Тарьян. Расширяющиеся деревья поддерживают баланс без
использования дополнительных полей (типа цвета). Вместо этого расширяющие
операции, включающие вращения, выполняются при каждом обращении к дереву.
Учетная стоимость в расчете на одну операцию с деревом для расширяющихся
деревьев составляет  .
.


 для
вставки элемента
для
вставки элемента  в
в  для
удаления
для
удаления