Приоритетные очереди

Нахождение кратчайших путей в графе

Входные данные:

• Граф со взвешенными ребрами (под весами можно понимать длины ребер, если речь идет о геометрическом графе, или любые другие числовые характеристики ребер). Пусть — вес ребра ( ).
• Стартовая вершина (вершина, от которой вычисляются расстояния до всех остальных вершин).

Выходные данные:

• Массив , — кратчайшее расстояние от вершины до вершины ).
• Массив , — предпоследняя вершина в кратчайшем пути из вершины в вершину ).

Приводимый ниже алгоритм Дейкстры корректно решает задачу для графов с неотрицательными весами вершин. Если же в графе есть ребра с отрицательными весами, но нет циклов с отрицательным суммарным весом, то для решения задачи можно использовать алгоритм Форда, Беллмана.

Алгоритм Дейкстры

1. Заполнить массив нулями.
2. Каждой вершине приписать в качестве ключа — максимально возможное число (оно должно быть больше, чем длина наибольшего из кратчайших путей в графе; в процессе вычислений это число будет уменьшаться и в итоге заменится на длину кратчайшего пути из вершины в вершину ).
3. Организовать приоритетную очередь из вершин графа, взяв в качестве ключей величины , .
4. Заменить ключ вершины на 0.
5. Пока очередь не пуста, выполнять операции .
6. Выбрать (с удалением) из приоритетной очереди элемент 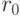с минимальным ключом.
7. Для каждой вершины , смежной с 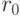, выполнить операции .
8. Вычислить величину .
9. Если , то уменьшить ключ элемента на величину и заменить старое значение величины на .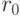

Упражнение

Напишите на каком-либо алгоритмическом языке реализацию алгоритма Дейкстры с использованием -кучи и испытайте ее на тестовых примерах при различных значениях .