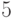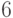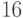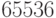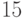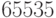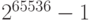|
на стр 6, лекции 3, Очевидно "Ck <= модуль(Gk(е))*b(k+1)" (1) - , подскажите что значит "модуль" и почему это очевидно... |
Разделенные множества
Представление разделенных множеств с использованием рангов вершин и сжатия путей
Предыдущий способ реализации разделенных множеств можно еще улучшить за
счет усовершенствования реализации операции НАЙТИ,( 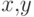 ).
Она теперь будет выполняться в два прохода. При первом проходе находится
корень
).
Она теперь будет выполняться в два прохода. При первом проходе находится
корень  того дерева, которому принадлежит
того дерева, которому принадлежит  . При
втором проходе из
. При
втором проходе из  в
в  все встреченные узлы делаются
непосредственными
потомками узла
все встреченные узлы делаются
непосредственными
потомками узла  . Этот прием, как мы увидим ниже, намного уменьшает
время выполнения последующих операций НАЙТИ.
. Этот прием, как мы увидим ниже, намного уменьшает
время выполнения последующих операций НАЙТИ.
Реализация операций. Рассматриваемая реализация не требует
новых полей данных по сравнению с предыдущим случаем. Как и прежде, для
каждого узла  будем хранить указатель
будем хранить указатель ![p[i]](/sites/default/files/tex_cache/8459deb7ccbe3cff4572f7200d484c8b.png) на его
родителя и ранг
на его
родителя и ранг ![r[i]](/sites/default/files/tex_cache/cb4368cce07a4fafb8bc7d516a768492.png) , который теперь не обязательно
будет равен высоте дерева с корнем
, который теперь не обязательно
будет равен высоте дерева с корнем  .
Он будет равен этой высоте, если не использовать операцию НАЙТИ.
.
Он будет равен этой высоте, если не использовать операцию НАЙТИ.
Операция СОЗДАТЬ
(  ) выполняется с помощью операторов
) выполняется с помощью операторов
![\formula{
\t begin p[x]:= x;\ r[x] := 0\
\t end;
}](/sites/default/files/tex_cache/035b50feb44514194c738146fdb90ed3.png)
В качестве родителя узла  берется тот же самый
берется тот же самый  , а его
рангом считаем
, а его
рангом считаем  . Таким образом, время выполнения операции есть
константа.
. Таким образом, время выполнения операции есть
константа.
Операция ОБЪЕДИНИТЬ
( 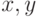 ) выполняется как и прежде,
разница лишь в том, что вместо массива
) выполняется как и прежде,
разница лишь в том, что вместо массива  используется
массив
используется
массив  .
Время выполнения операции — константа.
.
Время выполнения операции — константа.
![\formula{
\t{procedure ОБЪЕДИНИТЬ} (x,
y);\\
\tbegin\\
\mbox{}\q if\ (r[x] < r[y])\
then\ p[x] := y\
\t else\ \t if (r[x] > r[y])\ \t then\ p[y] := x\\
\mbox{}\q\t else \{p[x] := y;\ r[y]
:= r[y] + 1\} \\
\t end;
}](/sites/default/files/tex_cache/f7aaeb9c653e43fa423b6d713b5d1635.png)
Операция НАЙТИ 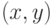 , как уже говорилось, выполняется в два прохода. При первом проходе мы идем от
узла
, как уже говорилось, выполняется в два прохода. При первом проходе мы идем от
узла  к его родителю, потом к родителю его родителя и так далее,
пока не достигнем корня у дерева, содержащего узел
к его родителю, потом к родителю его родителя и так далее,
пока не достигнем корня у дерева, содержащего узел  . При втором проходе
из
. При втором проходе
из  в
в  все встреченные на этом пути узлы делаются
непосредственными потомками узла
все встреченные на этом пути узлы делаются
непосредственными потомками узла  . Будем называть это "сжатием путей".
Очевидно, как и раньше, время выполнения одной такой операции есть
. Будем называть это "сжатием путей".
Очевидно, как и раньше, время выполнения одной такой операции есть  .
Но ниже будет доказано, что время выполнения
.
Но ниже будет доказано, что время выполнения  таких операций на
самом деле меньше, чем
таких операций на
самом деле меньше, чем 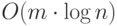 . Заметим, что при
выполнении этой операции ранги узлов не изменяются.
. Заметим, что при
выполнении этой операции ранги узлов не изменяются.
![\formula{
\t{procedure НАЙТИ}\ (x,y);\\
\t begin \\
\mbox{}\q z:= x;\ \t while\ (p[x]
\ne x)\ \t do\ x:= p[x];\\
\mbox{}\q y:= x;\ \t while\ (p[z]
\ne z)\ \t do\ \{z1:= z;\
z:= p[z];\ p[z1]:= y\} \\
\t end;
}](/sites/default/files/tex_cache/7cdd247f93546329ae28c5b54a7b0dfa.png)
Анализ трудоемкости
Для анализа трудоемкости выполнения операций нам потребуются две функции.
Одна из них,  , является суперэкспонентой и определяется
следующим образом:
, является суперэкспонентой и определяется
следующим образом:
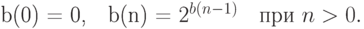
Вторая — суперлогарифм 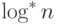 , по основанию 2,
определяемая соотношением
, по основанию 2,
определяемая соотношением
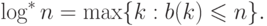
Суперлогарифм является в некотором смысле обратной функцией
к суперэкспоненте,  . Значения
функций
. Значения
функций 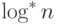 и
и  при нескольких значениях
аргументов приведены
в следующих таблицах:
при нескольких значениях
аргументов приведены
в следующих таблицах:
Ребро  при текущем состоянии коллекции назовем
корневым, если
при текущем состоянии коллекции назовем
корневым, если 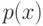 — корень и
— корень и 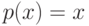 (петля);
назовем его прикорневым, если
(петля);
назовем его прикорневым, если 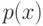 — корень и
— корень и  , в противном случае — внутренним.
, в противном случае — внутренним.
Отметим следующие свойства коллекции на множестве из  элементов.
Прикорневое ребро может превратиться во внутреннее, а корневое —
в прикорневое только при выполнении операции ОБЪЕДИНИТЬ.
элементов.
Прикорневое ребро может превратиться во внутреннее, а корневое —
в прикорневое только при выполнении операции ОБЪЕДИНИТЬ.
Внутреннее ребро  при первом же выполнении операции
НАЙТИ, "проходящей через него", исчезает, но вместо него появляется
прикорневое ребро
при первом же выполнении операции
НАЙТИ, "проходящей через него", исчезает, но вместо него появляется
прикорневое ребро  , при этом
, при этом 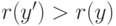 ,
следовательно, внутреннее ребро "участвует в поиске"
не более одного раза.
,
следовательно, внутреннее ребро "участвует в поиске"
не более одного раза.
Если при выполнении очередной операции
ОБЪЕДИНИТЬ  узел
узел  становится родителем
узла
становится родителем
узла  , то после ее выполнения
справедливо неравенство
, то после ее выполнения
справедливо неравенство 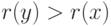 .
.
При выполнении операции НАЙТИ ранги узлов не изменяются, но узлы могут менять своих родителей, то есть меняется структура леса.
Если перед выполнением операции НАЙТИ узел  был родителем
узла
был родителем
узла  ,
а после выполнения этой операции родителем узла
,
а после выполнения этой операции родителем узла  стал
узел
стал
узел 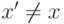 , то выполняется неравенство
, то выполняется неравенство 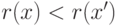 .
Следовательно, даже после изменения леса в результате
выполнения операции НАЙТИ ранги вдоль любого пути от листа к корню будут
строго возрастать.
.
Следовательно, даже после изменения леса в результате
выполнения операции НАЙТИ ранги вдоль любого пути от листа к корню будут
строго возрастать.
При выполнении операции ОБЪЕДИНИТЬ ранг любого некорневого элемента не изменяется, а ранг корня либо сохраняется, либо увеличивается на 1.