Деревья

Обходы деревьев

Часто при обработке представленной в дереве информации требуется обойти некоторым регулярным способом все его вершины. Имеется два естественных стандартных способа обхода деревьев. Каждый из них позволяет линейно упорядочить вершины дерева и тем самым представить его "двумерную структуру" в виде линейной последовательности вершин.

Прямой (префиксный) обход дерева основан на принципе: "сначала родитель, затем дети". Определим индукцией по построению дерева T в определении 10.3 его прямое представление ПР(T) следующим образом.

1. Если , то ПР(T₀)= v.
2. Если T получено из деревьев T₁, ..., T_k и нового корня r₀ по пункту (2) определения 10.3 то ПР(T)= r₀\, ПР(T₁)... ПР(T_k).

Обратный (суффиксный) обход дерева основан на противоположном принципе: "сначала дети , затем родитель". Вот его индуктивное определение.

1. 1) Если , то ОБР(T₀)= v.
2. 2) Если T получено из деревьев T₁, ..., T_k и нового корня r₀ по пункту (2) определения 10.3, то ОБР(T)= ОБР(T₁)... ОБР(T_k)\, r₀.

Для бинарных деревьев, внутренние вершины которых имеют не более 2-х сыновей, помеченных как "левый" и "правый", можно естественно определить еще один способ обхода - инфиксный (внутренний) обход, основанный на принципе: "сначала левый сын, затем родитель, а затем правый сын". Он определяется следующим образом.

1. Если , то ИНФ(T₀)= v.
2. Если T получено из деревьев T₁, T₂ и нового корня r₀ по пункту (2) определения 10.3, то ИНФ(T)= ИНФ(T₁) r₀ ИНФ(T₂)

(Если одно из деревьев T₁, T₂ пусто, то соответствующее ему инфиксное представление тоже пусто).

Пример 10.2. Построим в соответствии с этими определениями три разных обхода бинарного дерева , изображенного на рис. 10.4 (в скобках после вершины указана ее метка).

Для упорядоченного размеченного дерева T из класса по любому из указанных обходов ПР(T), ОБР(T) и, если дерево бинарное, - ИНФ(T) можно однозначно восстановить само дерево T (см. задачу 10,6).

Замечание. Для вычислительных приложений особенно интересен обратный обход, иногда называемый обратной польской записью. По нему компилятор легко строит программу вычисления соответствующего выражения.

Задачи

Задача 10.1. Докажите, что если в связном неориентированном графе число вершин равно числу ребер, то можно выбросить одно из ребер так, что после этого граф станет деревом.

Задача 10.2. Пусть G=(V, E) - неориентированное дерево и 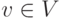- произвольная вершина. Докажите, что если для каждого ребра 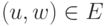выбрать ориентацию от u к w, если им заканчивается путь из v в w, и ориентацию от w к u, если им заканчивается путь из v в u, то полученный ориентированный граф будет ориентированным деревом с корнем v. Используйте это утверждение для доказательства следующего факта: если в неориентированном дереве G=(V, E) имеется вершина степени d >1, то в нем имеется по крайней мере d вершин степени 1.

Задача 10.3. Пусть T=(V,E) - это ориентированное дерево с корнем 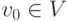. определим для каждой вершины 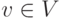подграф T_v=(V_v, E_v) следующим образом: V_v - это множество вершин, достижимых из v в T, а E_v - это множество ребер из E, оба конца которых входят в V_v. Доказать, что

• T_v является деревом с корнем v ;
• если две разные вершины v и u имеют одинаковую глубину, то деревья T_v и T_u не пересекаются.

Задача 10.4. Пусть G=(V,E) - ориентированный граф с n >1 вершинами. Докажите, что G является (ориентированным) деревом тогда и только тогда, когда в G нет циклов, имеется одна вершина r, в которую не входят ребра, а в каждую из остальных вершин входит ровно одно ребро.

Задача 10.5. Пусть корень ориентированного дерева T имеет 5 сыновей, а каждая из остальных внутренних вершин имеет три или четыре сына, при этом число вершин с 3-я сыновьями вдвое больше числа вершин с 4-я. Сколько всего вершин и ребер в T, если известно, что число его листьев равно 27?

Задача 10.6. Для каждого из обходов деревьев ПР(T), ОБР(T) и ИНФ(T) предложите процедуру, восстановления соответствующего дерева .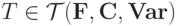

Задача 10.7. Докажите по индукции, что в любом бинарном дереве число вершин степени 2 на единицу меньше числа листьев.

Задача 10.8. Определите число листьев и число вершин в полном бинарном дереве высоты h.

Задача 10.9. Постройте дерево, представляющее следующую логическую формулу

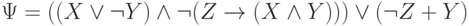
Для полученного дерева определите прямой, обратный и инфиксный обходы.

Задача 10.10. Постройте дерево и ациклический ориентированный граф, представляющие следующую арифметическую формулу

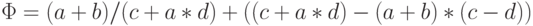
Сколько вершин удалось сократить?