|
Это в лекции 3. |
Язык логики предикатов
Задачи
Следующие четыре задачи относятся к системе \codecal{A}1 из примера 7.4 и ее состоянию  .
.
Задача 7.1.
Определите значение 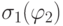 формулы
формулы 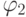 на состоянии
на состоянии 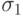 ,
отличающемся от
,
отличающемся от  только значением
только значением 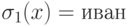 .
.
Задача 7.2.
Выделите в следующих формулах свободные и связанные вхождения переменных
и определите значения этих формул на состоянии  системы
системы 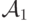 .
.
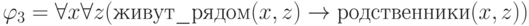
-
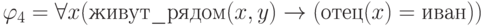 .
. ![\varphi _{5} = \forall u \exists v [живут\_ рядом(u, лучший_{д}руг(v)) \vee \setminus (зарплата(x) \le зарплата(v))]](/sites/default/files/tex_cache/c5e93211ffb8d5257a1b7c1171643915.png)
-
![\varphi _{6} = \exists v [\neg живут\_ рядом(v, z) \to (зарплата(отец(v) \le n)]](/sites/default/files/tex_cache/276c60d59efd6efcd351b6ca6b0ca663.png) .
.
Задача 7.3.
Запишите формулы, выражающие следующие свойства системы 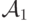 ,
и проверьте их истинность на этой системе.
,
и проверьте их истинность на этой системе.
- Рядом с каждым человеком А живет некто, отец которого является лучшим другом А.
- У каждого человека не более одного соседа.
- Если у соседа некоторого человека А зарплата больше чем у А, то этот сосед является родственником А.
- Есть человек, у которого не менее 2-х детей.
- Никто не является лучшим другом для более чем 2-х людей.
Задача 7.4.
Запишите формулы, которые истинны на состояниях  системы
системы 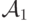 ,удовлетворяющих следующим условиям.
,удовлетворяющих следующим условиям.
-
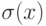 - человек, зарплата которого больше 20 и не больше 35.
- человек, зарплата которого больше 20 и не больше 35. -
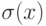 и
и 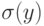 - это люди, у которых один и тот же лучший друг.
- это люди, у которых один и тот же лучший друг. -
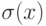 - человек с максимальной зарплатой, равной
- человек с максимальной зарплатой, равной  .
. -
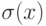 - человек, получающий большую зарплату, чем его отец.
- человек, получающий большую зарплату, чем его отец.
Найдите все значения переменных, на которых истинны соответствующие формулы.
Задача 7.5.
Арифметикой называется система 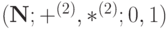 , где основное множество N={0, 1, 2, ...} - множество натуральных чисел, функции + и * - обычное сложение и умножение, а 0 и 1 - соответствующие числа.
, где основное множество N={0, 1, 2, ...} - множество натуральных чисел, функции + и * - обычное сложение и умножение, а 0 и 1 - соответствующие числа.
Запишите формулы со свободными переменными из { x, y, z}, которые истинны в арифметике тогда и только тогда, когда
- x меньше y ;
- x является четным числом;
- y является простым числом;
- x и y взаимно просты;
- z лежит в интервале между x и y ;
- сложение (умножение) коммутативно;
- существует бесконечно много простых чисел.
Задача 7.6. Представьте каждое из следующих предложений формулой логики предикатов, определив в каждом случае подходящую сигнатуру.
- Не все студенты изучают и анализ, и историю.
- Только один студент не сдал экзамен по дискретной математике.
- Только один студент сдал все экзамены на отлично.
- Максимальные баллы, полученные по дискретной математике, превышают максимальные баллы, полученные по информатике.
- Каждый, кто не любит всех вегетарианцев, является странным человеком.
- Имеется брадобрей, бреющий только тех жителей города, которые не бреются сами.
- Политики могут обманывать всех людей некоторое время, они могут обманывать некоторых людей все время, но они не могут обманывать всех людей все время.
Задача 7.7. Напишите формулу логики предикатов, истинной только на всех системах, основное множество которых состоит из одного элемента (2-х , 3-х,..., k элементов).
Задача 7.8. Докажите правило замены эквивалентных подформул, используя индукцию по построению формул и подформул.
Задача 7.9. Проведите доказательство эквивалентностей (2) - (8).
Задача 7.10. Доказажите следующие эквивалентности, показывающие, что одноименные кванторы можно менять местами:
-
 ,
, -
 .
.
Задача 7.11. Докажите, что разноименные кванторы менять местами нельзя, т.е., что формулы  и
и 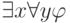 не эквивалентны.
не эквивалентны.
Задача 7.12.
Приведите к предваренной нормальной форме следующие формулы, считая,
что  и
и  - бескванторные.
- бескванторные.
-
 ,
, -
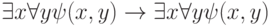 ,
, -
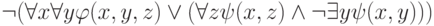 .
.
