Предварительные сведения

Задачи

Задача 1.1. Доказать следующие включения:

• ;
• 

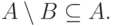
Задача 1.2. Доказать следующие тождества:

• ;
• ;
• ;
• ;
• ;
• ;
• ;
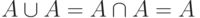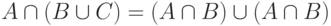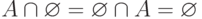• и

Задача 1.3. Найти все подмножества множеств 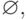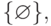{1,2,3},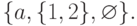

Задача 1.4. Пусть A={ 0, 1}, B ={a,b,c}. Определите множества Ax B и B x A.

Задача 1.5. Доказать, что

• ;
• ;
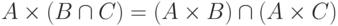• A x (B \ C) = (Ax B)\ (Ax C) ;
• если и то

Задача 1.6. Для каждого из следующих отношений определить :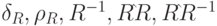

• ;
• ;
• ;
• ;
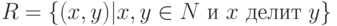• R = {(a,b), (b,c), (b,d), (c,d), (d, b)}.

Задача 1.7. Пусть множество S ={ (i, j) | 1<= i, j <= 8} задает клетки шахматной доски. Опишите следующие бинарные отношения на S:

• L ={ (a,b) | ладья за 1 ход может перейти с клетки a на клетку b };
• K= { (a,b) | конь за 1 ход может перейти с клетки a на клетку b }.

Будут ли эти отношения эквивалентностями? Опишите отношение

Задача 1.8. Пусть - множество прямых на плоскости. Будут ли следующие отношения отношениями эквивалентности:

• параллельность прямых;
• перпендикулярность прямых.

Задача 1.9. Пусть A={a₁,..., a_m} - произвольный конечный алфавит. Обозначим через Aⁿ множество слов длины n в алфавите A (это обозначение согласовано с тем же обозначением декартовой степени A, так как степень Aⁿ состоит из всех последовательностей элементов A длины n ). Через A^* обозначим множество всех слов в алфавите A.

• Определим следующее отношение R₁ на словах из Aⁿ.

  Пусть v=a_{i₁}a_{i₂}... a_{i_n}, 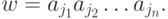Тогда

  для всех k от 1 до n i_k <= j_k и для некоторого такого k i_k < j_k, т.е. номер каждой буквы слова v не больше номера той же буквы в слове w и хотя бы у одной из букв он меньше.

  Является ли это отношение R₁ отношением частичного (линейного) порядка?

• Определим следующее отношение R₂ на словах из A^*.

  Пусть v=a_{i₁}a_{i₂}... a_{i_n}, Тогда

  существует такое k в интервале от 1 до n, что при l < k i_l = j_l и i_k < j_k или n < r и первые n символов w совпадают со словом v.

  Является ли это отношение R₂ отношением частичного (линейного) порядка?

Замечание. Определенное в пункте (а) отношение R₁ называется отношением покоординатного порядка, а отношение R₂ из пункта (б) - отношением лексикографического порядка. В соответствии с лексикографическим порядком упорядочены, например, слова в словарях и энциклопедиях.

Задача 1.10. Доказать, что если множества A и B конечны, то

• | A x B| = |A| x |B|;
•