| Россия |
Оптимальная разделяющая гиперплоскость
4.2. Построение оптимальной разделяющей гиперплоскости
Теорема. Если два множества  и
и  разделимы гиперплоскостью,
разделимы гиперплоскостью,  и
и  – выпуклые оболочки этих множеств, а
– выпуклые оболочки этих множеств, а  и
и  – пара ближайших точек в выпуклых оболочках, то
– пара ближайших точек в выпуклых оболочках, то
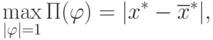
 – обозначает евклидово расстояние между точками
– обозначает евклидово расстояние между точками 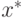 и
и 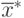 .
.Доказательство. Положим  .
Из условий
.
Из условий  , следует, что
, следует, что 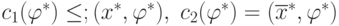 и,
следовательно,
и,
следовательно,
 |
( 4.2) |
 и для доказательства теоремы нужно показать, что справедливо неравенство
и для доказательства теоремы нужно показать, что справедливо неравенство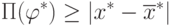 |
( 4.3) |
Пусть точки 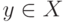 и
и  такие,
что
такие,
что  и
и 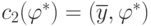 .
Тогда
.
Тогда

Теперь покажем, что 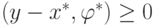 ,
а
,
а 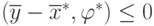 , или, что то же самое:
, или, что то же самое:
 |
( 4.4) |
 – точка в
– точка в 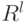 .
Очевидно, что она лежит в выпуклой оболочке
.
Очевидно, что она лежит в выпуклой оболочке  , т.е.
, т.е.  . Тогда имеем
. Тогда имеем |
( 4.5) |
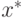 и
и 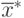 –
ближайшие в выпуклых оболочках
–
ближайшие в выпуклых оболочках  и
и  ,
получаем, что
,
получаем, что  . Тогда из (4.5) следует, что
. Тогда из (4.5) следует, что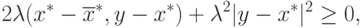
 ,
что возможно лишь при
,
что возможно лишь при  .
Таким образом, первое из неравенств (4.4) доказано.
Второе неравенство (4.4) доказывается аналогично.
.
Таким образом, первое из неравенств (4.4) доказано.
Второе неравенство (4.4) доказывается аналогично.Тем самым доказано неравенство (4.3), а из него (4.2) и утверждение теоремы.
Оптимальная разделяющая гиперплоскость ортогональна отрезку,
соединяющему ближайшие точки выпуклых оболочек множеств  и
и  , и проходит через середину этого отрезка.
Задача поиска пары ближайших точек сводится к задаче квадратичного
программирования следующим образом.
, и проходит через середину этого отрезка.
Задача поиска пары ближайших точек сводится к задаче квадратичного
программирования следующим образом.
Каждая точка  , лежащая в выпуклой оболочке
, лежащая в выпуклой оболочке  , представима в виде
, представима в виде  .
Аналогично, точка
.
Аналогично, точка  представима в виде
представима в виде  .
Нужно найти пару точек
.
Нужно найти пару точек  и
и  , обеспечивающих минимум выражения:
, обеспечивающих минимум выражения:
 |
( 4.6) |
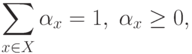 |
( 4.7) |
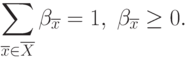 |
( 4.8) |
4.3. Алгоритм Гаусса-Зейделя
Задача состоит в нахождении наименьшего расстояния между множествами  и
и  .
.
1. В качестве начальных значений берем произвольную пару  и
и 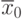 .
Другими словами в начальный момент
.
Другими словами в начальный момент  и
и  .
.
2. Необходимо найти точку 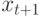 ближайшую к
ближайшую к  на отрезке
на отрезке ![[z_t,x_t]](/sites/default/files/tex_cache/df1b93082bc508620c2bf8aaefec6bd6.png) . Обозначаем
. Обозначаем  .
Напишем условие ортогональности векторов
.
Напишем условие ортогональности векторов  и
и  :
:

 , то
, то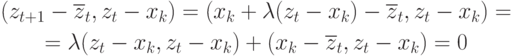
 .
Если
.
Если  , то
, то  .
Если
.
Если  , то
, то  .
Если
.
Если 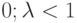 , то
, то 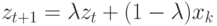 .
.3. Далее необходимо найти точку  ближайшую к
ближайшую к  на отрезке
на отрезке ![[\overline{z}_t,x_r]](/sites/default/files/tex_cache/c45763dea233e16aac4ca0d3b75b3e39.png) . Обозначаем
. Обозначаем  .
.
Данную процедуру необходимо повторять, пока не найдутся две
ближайшие точки множеств  и
и  .
.

