| Россия |
Линейный классификатор. Алгоритм персептрона
3.2.3. Сходимость алгоритма персептрона.
Основной вопрос, связанный с алгоритмом персептрона связан с его сходимостью. Конечен ли построенный итерационный процесс обучения?
Теорема Новикова. Пусть 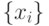 – бесконечная последовательность векторов из двух непересекающихся
замкнутых множеств
– бесконечная последовательность векторов из двух непересекающихся
замкнутых множеств  и
и  ; и пусть существует гиперплоскость,
проходящая через начало координат и разделяющая
; и пусть существует гиперплоскость,
проходящая через начало координат и разделяющая  и
и  (не имеет с ними
общих точек). Тогда при использовании алгоритма персептрона число
коррекций весового вектора конечно.
(не имеет с ними
общих точек). Тогда при использовании алгоритма персептрона число
коррекций весового вектора конечно.
Доказательство. Пусть 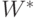 - направляющий вектор разделяющей
гиперплоскости (которая существует по условию). Не нарушая общности,
будем считать, что он является единичным.
- направляющий вектор разделяющей
гиперплоскости (которая существует по условию). Не нарушая общности,
будем считать, что он является единичным.
Пусть 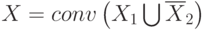 ,
, 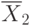 в – симметричное
к
в – симметричное
к  множество;
множество; 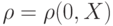 , где
, где  – евклидово
расстояние. Согласно утверждению 3.3
– евклидово
расстояние. Согласно утверждению 3.3 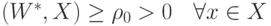 .
.
Оценим  .
.
Пусть 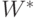 – единичный вектор нормали, разделяющий
– единичный вектор нормали, разделяющий  и
и  .
.
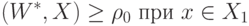

Пусть 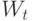 – весовой вектор после предъявления вектора
– весовой вектор после предъявления вектора 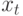 ;
; 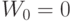 – начальная итерация весового вектора
– начальная итерация весового вектора 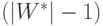 .
Тогда, если
.
Тогда, если 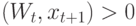 , то коррекции не происходит.
Иначе, если
, то коррекции не происходит.
Иначе, если 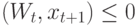 , то коррекция:
, то коррекция: 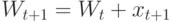
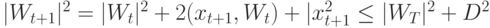 , т.к.
, т.к. 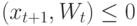 и
и 
Таким образом, к моменту  происходит
происходит  коррекций, то
коррекций, то
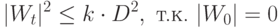 |
( 3.1) |
В начальный момент времени  .
Если в момент
.
Если в момент  произошла коррекция, то
произошла коррекция, то
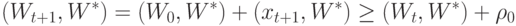
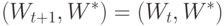
 произошло
произошло  коррекций, то
коррекций, то

 |
( 3.2) |
Из неравенств 3.1 и 3.2 следует:
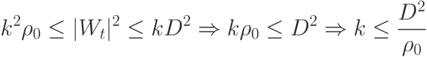
 не превосходит
не превосходит 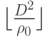 .
.3.2.4. Оптимизационная интерпретация. Рассмотрим непрерывную кусочно-линейную функцию  :
:
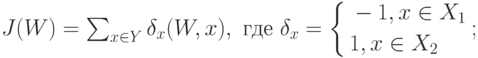
 – множество векторов неправильно классифицированных гиперплоскостью
– множество векторов неправильно классифицированных гиперплоскостью  .
Тогда
.
Тогда 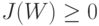 и
и 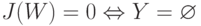 . Задача состоит в минимизации этой функции:
. Задача состоит в минимизации этой функции: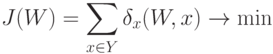
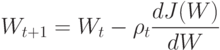
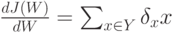 , то
, то 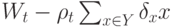
Таким образом, алгоритм персептрона представляет собой вариант
алгоритма градиентного спуска. Выбор последовательности величин 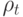 для
обычно осуществляется так, чтобы:
для
обычно осуществляется так, чтобы:
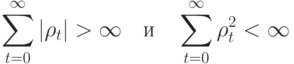
3.2.5. Схема Кеслера. Идея построения линейного классификатора
естественно обобщается на случай классификации с числом классов больше
двух. Рассмотрим задачу классификации по  классам. Для каждого класса
необходимо определить линейную дискриминантную функцию
классам. Для каждого класса
необходимо определить линейную дискриминантную функцию 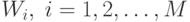 .
Пусть –
.
Пусть – 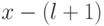 -мерный вектор в расширенном пространстве. Вектор
-мерный вектор в расширенном пространстве. Вектор  относится к
классу
относится к
классу  , если
, если
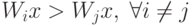
Схема Кеслера позволяет применить алгоритм персептрона для решения этой задачи.
Для каждого вектора-прецедента из 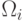 строим
строим 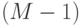 векторов
векторов 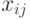 размерности
размерности 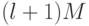 :
:
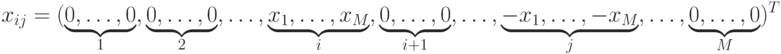
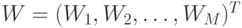 , где
, где  – весовой вектор
– весовой вектор  -ой
дискриминантной функции.
-ой
дискриминантной функции.Пусть 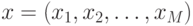 , тогда вектор
, тогда вектор 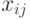 можно записать в виде:
можно записать в виде:
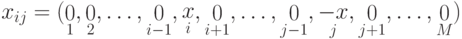
Если  относится к классу
относится к классу 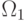 , то
, то 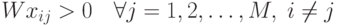 , т.к.
, т.к. 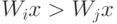 и
и 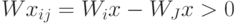 .
.
Таким образом, задача заключается в построении линейного
классификатора в 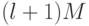 -мерном пространстве так, чтобы каждый из
-мерном пространстве так, чтобы каждый из  векторов-прецедентов лежал в положительном полупространстве. Если
вектора в исходной задаче разделимы, то это можно сделать с помощью
алгоритма персептрона.
векторов-прецедентов лежал в положительном полупространстве. Если
вектора в исходной задаче разделимы, то это можно сделать с помощью
алгоритма персептрона.